Trong toán học, Định lý Talet đảo trong tam giác là một công cụ quan trọng giúp chúng ta xác định mối quan hệ song song giữa các đường thẳng và các cạnh của tam giác. Nắm vững định lý này không chỉ giúp giải các bài tập hình học hiệu quả mà còn là nền tảng cho nhiều khái niệm toán học phức tạp hơn. Bài viết này sẽ cung cấp kiến thức chi tiết về Định lý Talet và định lý đảo của nó, cùng với các hệ quả và bài tập minh họa để bạn đọc có thể hiểu sâu và áp dụng thành thạo.

Đề Bài

<?xml encoding=”utf-8″ ?><?xml encoding=”utf-8″ ?> Home » Toán Học » Định lý Talet và Talet đảo trong Tam Giác, Tam Giác Vuông Toán Lớp 8

Toán Học

Định lý Talet và Talet đảo trong Tam Giác, Tam Giác Vuông Toán Lớp 8

admin.ta 22 Tháng Mười, 2025

381 Views 0

SaveSavedRemoved 1

dinh ly taletĐịnh lý Talet trong tam giác thường và tam giác vuông có tính chất như thế nào ? Định lý đảo và Hệ quả của định lý Talet sẽ có tính chất như thế nào ?

Cùng theo dõi bài viết dưới đây để tìm ngay đáp án giải đáp nhé !

Tham khảo bài viết khác:

Định lý Talet trong tam giác

– Phát biểu bằng lời: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lai thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.

dinh ly talet

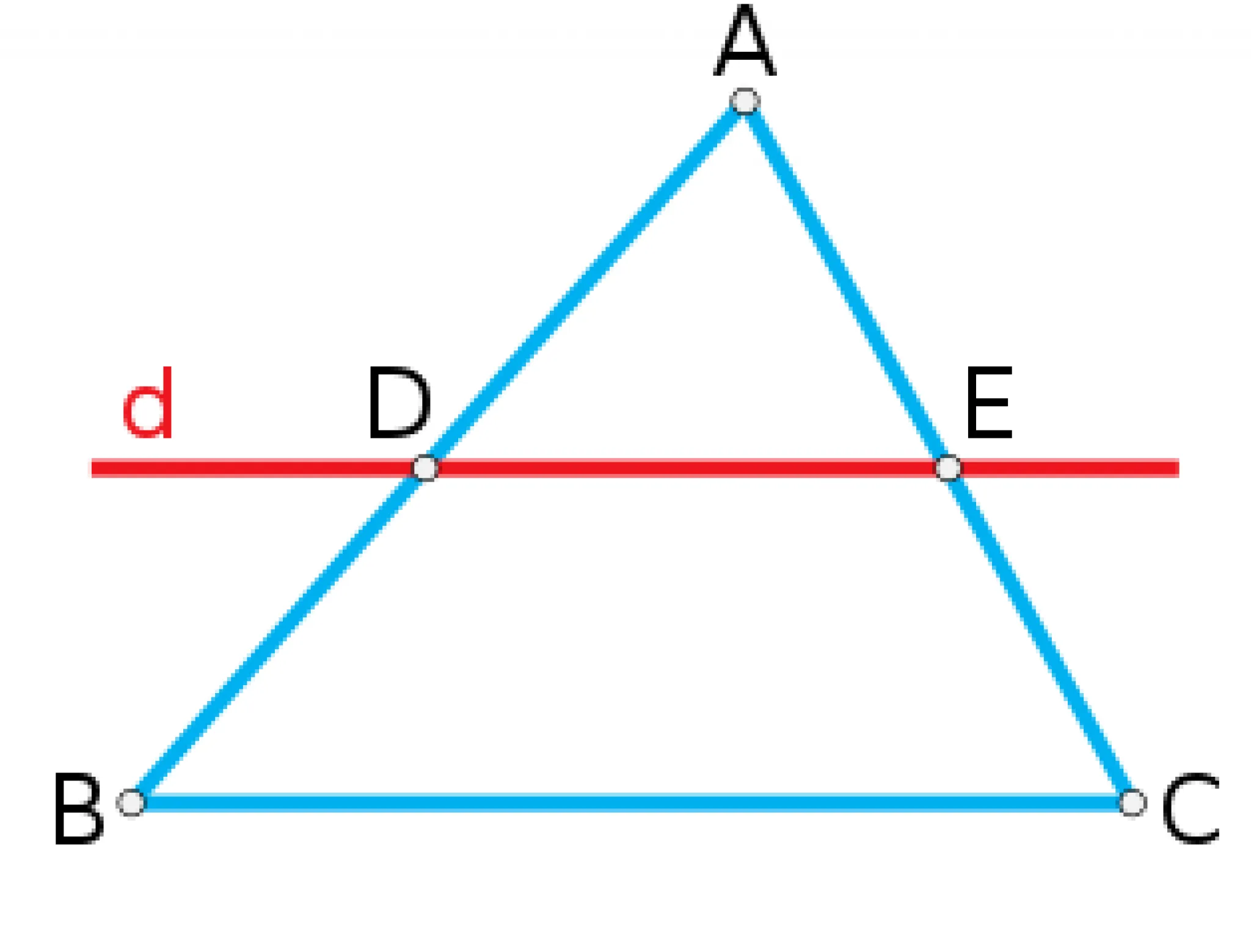
Tại hình vẽ bên nếu có: tam giác ABC – d cắt AB tại D, cắt AC tại E, song song với BC. Như vậy theo định lý Talet ta có được

dinh ly talet trong tam giac

Định lí Ta-lét đảo trong tam giác

– Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

dinh ly talet

Tại hình vẽ bên nếu có: tam giác ABC dinh ly talet dao ==> Như vậy theo định lý Talet đảo, ta có được: DE song song với BC ( DE//BC ).

Hệ quả của định lý Talet trong Tam giác

+) Hệ quả 1

– Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì sẽ tạo ra một tam giác mới có ba cạnh tỉ lệ với ba cạnh của tam giác đã cho.

+) Hệ quả 2

– Có một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì sẽ tạo ra một tam giác mới đồng dạng với tam giác đã cho.

+) Hệ quả 3 – Talet mở rộng

– Talet mở rộng được phát biểu như sau: Ba đường thẳng đồng quy thì chắn trên hai đường thẳng song song các cặp đoạn thẳng tỉ lệ.

he qua dinh ly talet

Bài tập minh họa Định lý Talet

Bài tập 1: Cho biết độ dài cùa AB gấp 5 lần độ dài của CD và độ dài của A’B’ gấp 12 lần độ dài của CD. Tính tỉ số của hai đoạn thẳng AB và A’B’.

Hướng dẫn giải:

Độ dài AB gấp 5 lần độ dài CD nên AB= 5CD.

Độ dài A’B’ gấp 12 lần độ dài CD nên A’B’= 12CD.

=> Tí số của hai đoạn thẳng AB và A’B’ là:

vi du dinh ly ta let

Hy vọng bài viết này sẽ đem đến những nội dung hữu ích cho bạn. Cám ơn bạn đã theo dõi bài viết của chúng tôi, tiếp tục theo dõi trang web ở những bài viết tiếp theo của chúng tôi.

Người xem: 1.411

Phân Tích Yêu Cầu

Bài viết gốc trình bày về Định lý Talet, Định lý Talet đảo và các hệ quả trong tam giác, kèm theo một ví dụ minh họa. Mục tiêu là làm rõ các khái niệm này và cách áp dụng chúng. Các phần chính bao gồm phát biểu định lý, hình minh họa và một bài tập có hướng dẫn giải.

Kiến Thức/Nền Tảng Cần Dùng

Để hiểu và áp dụng Định lý Talet đảo trong tam giác, chúng ta cần nắm vững các kiến thức sau:

• Định lý Talet (thuận): Phát biểu định lý, cách ghi tỉ lệ thức tương ứng giữa các đoạn thẳng. Nếu đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại, nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ. Cụ thể, với tam giác ABC và đường thẳng DE song song với BC (D thuộc AB, E thuộc AC), ta có tỉ lệ:
  \dfrac{AD}{AB} = \dfrac{AE}{AC} = \dfrac{DE}{BC}
  hoặc
  \dfrac{AD}{DB} = \dfrac{AE}{EC}

• Tỉ lệ thức: Hiểu rõ khái niệm tỉ lệ thức, các tính chất cơ bản của tỉ lệ thức.

• Khái niệm đoạn thẳng tương ứng tỉ lệ: Các đoạn thẳng có độ dài theo một tỉ lệ nhất định.

Hướng Dẫn Giải Chi Tiết

1. Phát biểu Định lý Talet đảo

Định lý Talet đảo là mệnh đề đảo của Định lý Talet. Nó cho phép chúng ta suy ra tính song song từ tỉ lệ thức của các đoạn thẳng.

• Phát biểu: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ, thì đường thẳng đó song song với cạnh còn lại của tam giác.

• Chứng minh (với hình vẽ tương tự Định lý Talet):
  Giả sử tam giác ABC có đường thẳng d cắt hai cạnh AB và AC lần lượt tại D và E.
  Nếu ta có tỉ lệ thức: \dfrac{AD}{AB} = \dfrac{AE}{AC} (hoặc \dfrac{AD}{DB} = \dfrac{AE}{EC}), thì theo Định lý Talet đảo, ta suy ra được đường thẳng DE song song với cạnh BC (tức là DE // BC).

  dinh ly talet dao

2. Hệ quả của Định lý Talet

Định lý Talet và Định lý Talet đảo còn có các hệ quả quan trọng giúp mở rộng ứng dụng:

• Hệ quả 1: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại, nó tạo ra một tam giác mới có ba cạnh tỉ lệ với ba cạnh của tam giác đã cho.
  Nếu DE // BC với D thuộc AB, E thuộc AC, thì tam giác ADE đồng dạng với tam giác ABC.

• Hệ quả 2: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại sẽ tạo ra một tam giác mới đồng dạng với tam giác ban đầu.
  Nếu DE // BC, thì triangle ADE \sim triangle ABC.

• Hệ quả 3 (Talet mở rộng): Ba đường thẳng đồng quy (cắt nhau tại một điểm) chắn trên hai đường thẳng song song bất kỳ các cặp đoạn thẳng tương ứng tỉ lệ.

  he qua dinh ly taletNếu ba đường thẳng cắt nhau tại O và chắn hai đường thẳng song song a, b tại các điểm A, B (trên a) và A’, B’ (trên b), thì `\dfrac{OA}{OA'} = \dfrac{OB}{OB'}`.

3. Bài tập minh họa Định lý Talet

Bài tập 1: Cho biết độ dài của AB gấp 5 lần độ dài của CD và độ dài của A’B’ gấp 12 lần độ dài của CD. Tính tỉ số của hai đoạn thẳng AB và A’B’.

Hướng dẫn giải:

Theo đề bài, ta có các mối quan hệ về độ dài:
Độ dài AB gấp 5 lần độ dài CD nên AB = 5 times CD.
Độ dài A’B’ gấp 12 lần độ dài CD nên A’B’ = 12 times CD.

Để tính tỉ số của hai đoạn thẳng AB và A’B’, ta lập tỉ lệ:
\dfrac{AB}{A’B’} = \dfrac{5 \times CD}{12 \times CD}

Rút gọn CD ở cả tử và mẫu, ta được:
\dfrac{AB}{A’B’} = \dfrac{5}{12}

Kết quả: Tỉ số của hai đoạn thẳng AB và A’B’ là \dfrac{5}{12}.

Mẹo kiểm tra: Khi gặp bài toán về tỉ lệ độ dài, hãy cố gắng biểu diễn tất cả các đại lượng qua một đại lượng chung (ở đây là CD) để dễ dàng rút gọn và tìm tỉ số cuối cùng.

Lỗi hay gặp:

• Nhầm lẫn giữa tỉ lệ đoạn thẳng và tỉ lệ giữa đoạn thẳng với cạnh ban đầu (ví dụ: dùng AD/DB thay vì AD/AB khi chưa phù hợp).
• Quên rút gọn hoặc tính toán sai khi lập tỉ lệ.

Đáp Án/Kết Quả

Định lý Talet đảo là một công cụ mạnh mẽ để xác định sự song song dựa trên tỉ lệ của các đoạn thẳng. Khi một đường thẳng cắt hai cạnh của tam giác và tạo ra các đoạn thẳng tương ứng tỉ lệ, đường thẳng đó chắc chắn song song với cạnh còn lại. Các hệ quả của định lý này còn mở rộng khả năng áp dụng vào việc chứng minh sự đồng dạng của các tam giác và giải quyết các bài toán về tỉ lệ trên các đường thẳng cắt nhau. Bài tập minh họa đã cho thấy cách áp dụng đơn giản định lý này để tìm tỉ lệ giữa các đoạn thẳng.

Nắm vững Định lý Talet đảo trong tam giác là một bước tiến quan trọng trong việc chinh phục hình học lớp 8 và các cấp học cao hơn. Bằng cách hiểu rõ phát biểu, các hệ quả và thực hành qua các bài tập, bạn sẽ tự tin hơn khi giải quyết các vấn đề liên quan đến tỉ lệ và sự song song trong hình học.

Ngày chỉnh sửa nội dung mới nhất January 8, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.