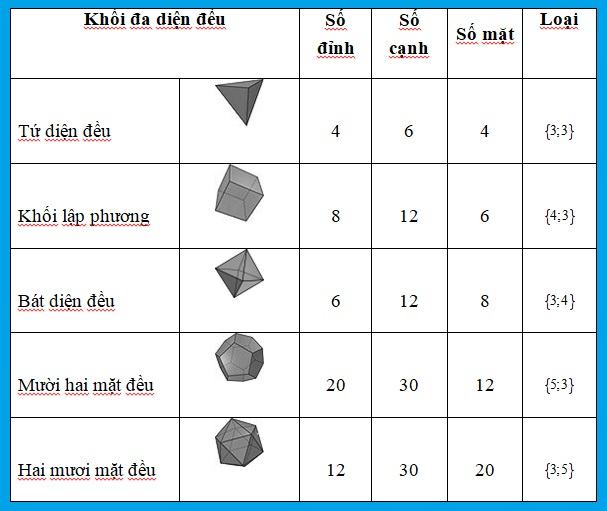
Khái Niệm Về Khối Đa Diện Và Khối Đa Diện Lồi, Đều Trong Toán Lớp 12
Giới Thiệu
Chào mừng bạn đến với chuyên mục giải bài tập Toán lớp 12 về khái niệm về khối đa diện. Trong bài viết này, chúng ta sẽ cùng nhau khám phá định nghĩa, các tính chất cơ bản của khối đa diện, cũng như phân biệt giữa khối đa diện lồi và khối đa diện đều. Đây là những kiến thức nền tảng quan trọng cho chương trình Hình học lớp 12, giúp bạn xây dựng nền tảng vững chắc để chinh phục các dạng bài tập phức tạp hơn. Chúng ta sẽ đi sâu vào phân tích từng câu hỏi và bài tập trong Sách Giáo Khoa, đảm bảo bạn hiểu rõ bản chất và cách áp dụng.

Đề Bài: Khái Niệm Về Khối Đa Diện
Câu hỏi Toán 12 Hình học Bài 1 trang 4: Nhắc lại định nghĩa hình lăng trụ và hình chóp.
Phân Tích Yêu Cầu:
Câu hỏi này yêu cầu chúng ta ôn lại định nghĩa cơ bản về hai loại hình không gian quen thuộc: hình lăng trụ và hình chóp. Đây là bước đầu tiên để hiểu về các khối đa diện.
Kiến Thức/Nền Tảng Cần Dùng:
- Hình lăng trụ: Là hình có hai đáy là hai đa giác bằng nhau và nằm trên hai mặt phẳng song song. Các mặt bên của hình lăng trụ là các hình bình hành, và các cạnh bên song song hoặc bằng nhau.
- Hình chóp: Là hình không gian có một mặt đáy là một đa giác, và các mặt bên là các tam giác có chung một đỉnh gọi là đỉnh của hình chóp.
Hướng Dẫn Giải Chi Tiết:
Dựa trên kiến thức đã học, chúng ta có thể định nghĩa lại như sau:
- Hình lăng trụ: Là một khối đa diện lồi, được tạo thành bởi hai đa giác đáy bằng nhau và nằm trên hai mặt phẳng song song, cùng với các mặt bên là hình bình hành nối các cạnh tương ứng của hai đáy. Các cạnh nối hai đáy được gọi là cạnh bên và chúng song song, bằng nhau.
- Hình chóp: Là một khối đa diện lồi, bao gồm một mặt đáy là một đa giác và một đỉnh nằm ngoài mặt phẳng chứa đáy. Các mặt bên là các tam giác nối đỉnh chung với các cạnh của đa giác đáy.
Mẹo Kiểm Tra: Hãy tưởng tượng các hình dạng này trong không gian. Hình lăng trụ có hai “tầng” giống hệt nhau, còn hình chóp thì “nhọn” dần về một đỉnh.
Lỗi Hay Gặp: Nhầm lẫn giữa hình lăng trụ và hình chóp, hoặc không phân biệt rõ các mặt đáy và mặt bên.
Câu hỏi Toán 12 Hình học Bài 1 trang 6: Kể tên các mặt của hình lăng trụ ABCDE.A’B’C’D’E’ và hình chóp S.ABCDE (h.1.4).
Phân Tích Yêu Cầu:
Yêu cầu này đòi hỏi chúng ta phải xác định và liệt kê tất cả các mặt (đáy và mặt bên) của hai hình cụ thể đã cho.
Kiến Thức/Nền Tảng Cần Dùng:
- Định nghĩa hình lăng trụ và hình chóp.
- Cách xác định mặt đáy và mặt bên dựa trên ký hiệu của hình.
Hướng Dẫn Giải Chi Tiết:
Chúng ta sẽ xem xét từng hình:
-
Hình lăng trụ ABCDE.A’B’C’D’E’:
- Hai mặt đáy là hai đa giác:
ABCDEvàA’B’C’D’E’. - Các mặt bên là các hình bình hành nối các cạnh tương ứng của hai đáy:
ABB’A’,BCC’B’,CDD’C’,DEE’D’,EAA’E’. - Tổng cộng có 7 mặt.
- Hai mặt đáy là hai đa giác:
-
Hình chóp S.ABCDE:
- Mặt đáy là đa giác
ABCDE. - Đỉnh của chóp là
S. - Các mặt bên là các tam giác nối đỉnh
Svới các cạnh của đáy:SAB,SBC,SCD,SDE,SAE. - Tổng cộng có 6 mặt.
- Mặt đáy là đa giác
Mẹo Kiểm Tra: Đối với hình lăng trụ, số mặt bên bằng số cạnh của đa giác đáy. Đối với hình chóp, số mặt bên bằng số cạnh của đa giác đáy.
Lỗi Hay Gặp: Bỏ sót mặt đáy hoặc mặt bên, hoặc nhầm lẫn ký hiệu các đỉnh.
Câu hỏi Toán 12 Hình học Bài 1 trang 8: Giải thích tại sao hình 1.8c không phải là một khối đa diện?
Phân Tích Yêu Cầu:
Câu hỏi này đi sâu vào một tính chất quan trọng của khối đa diện: tính chất về cạnh. Chúng ta cần giải thích dựa trên định nghĩa hoặc tính chất này.
Kiến Thức/Nền Tảng Cần Dùng:
- Tính chất của khối đa diện: Mỗi cạnh của một khối đa diện là cạnh chung của đúng hai mặt.
Hướng Dẫn Giải Chi Tiết:
Quan sát hình 1.8c (trong SGK, giả định hình này có cạnh AB là cạnh chung của nhiều hơn hai mặt), ta thấy cạnh AB không phải là cạnh chung của đúng hai mặt. Thay vào đó, cạnh AB này là cạnh chung của bốn mặt đa giác khác nhau. Điều này vi phạm tính chất cơ bản của khối đa diện. Do đó, hình 1.8c không phải là một khối đa diện.
Mẹo Kiểm Tra: Hãy tưởng tượng bạn đang lắp ghép các mặt của khối đa diện. Nếu một cạnh bị “lộ ra” hoặc là điểm gặp của quá nhiều mặt, đó có thể không phải là khối đa diện hợp lệ.
Lỗi Hay Gặp: Không nhớ hoặc không hiểu rõ tính chất “mỗi cạnh là cạnh chung của đúng hai mặt”.
Câu hỏi Toán 12 Hình học Bài 1 trang 10: Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng hai lăng trụ ABD.A’B’D’ và BCD.B’C’D’ bằng nhau.
Phân Tích Yêu Cầu:
Chúng ta cần chứng minh hai lăng trụ cụ thể được tạo ra từ hình hộp là bằng nhau. Điều này thường được chứng minh bằng cách sử dụng phép đối xứng hoặc phép dời hình.
Kiến Thức/Nền Tảng Cần Dùng:
- Định nghĩa hình hộp.
- Khái niệm về phép đối xứng qua mặt phẳng.
- Điều kiện để hai khối đa diện bằng nhau (chúng có thể được biến đổi thành nhau qua một phép dời hình).
Hướng Dẫn Giải Chi Tiết:
Xét hình hộp ABCD.A’B’C’D’.
Hai lăng trụ được đề cập là:
- Lăng trụ
ABD.A’B’D’(có đáy là tam giácABDvàA’B’D’). - Lăng trụ
BCD.B’C’D’(có đáy là tam giácBCDvàB’C’D’).
Ta nhận thấy rằng mặt phẳng (BDD’B’) là mặt phẳng đối xứng của hình hộp ABCD.A’B’C’D’. Phép đối xứng qua mặt phẳng (BDD’B’) sẽ biến điểm A thành điểm C và biến điểm A’ thành điểm C’. Đồng thời, nó giữ nguyên các điểm B, D, B’, D’.
Do đó, phép đối xứng qua mặt phẳng (BDD’B’) biến tam giác ABD thành tam giác CBD (hay BCD) và biến tam giác A’B’D’ thành tam giác C’B’D’ (hay B’C’D’).
Vì phép đối xứng là một phép dời hình, nó bảo toàn khoảng cách và hình dạng. Do đó, phép đối xứng qua mặt phẳng (BDD’B’) biến lăng trụ ABD.A’B’D’ thành lăng trụ BCD.B’C’D’.
Suy ra, hai lăng trụ ABD.A’B’D’ và BCD.B’C’D’ bằng nhau.
Mẹo Kiểm Tra: Hãy hình dung mặt phẳng (BDD’B’) như một tấm gương. Nó phản chiếu phần bên trái của hình hộp sang bên phải và ngược lại.
Lỗi Hay Gặp: Không xác định đúng mặt phẳng đối xứng hoặc không hiểu phép đối xứng biến hình như thế nào.
Bài 1 (trang 12 SGK Hình học 12): Chứng minh rằng một đa diện có các mặt là những tam giác thì tổng số các mặt của nó phải là một số chẵn. Cho ví dụ.
Phân Tích Yêu Cầu:
Bài toán này yêu cầu chứng minh một tính chất liên quan đến số mặt của đa diện khi tất cả các mặt đều là tam giác, và đưa ra một ví dụ minh họa.
Kiến Thức/Nền Tảng Cần Dùng:
- Định nghĩa khối đa diện.
- Tính chất mỗi cạnh là cạnh chung của đúng hai mặt.
- Quan hệ giữa số mặt, số cạnh và số đỉnh của khối đa diện (Công thức Euler: V – E + F = 2, tuy nhiên ở đây ta chỉ cần tập trung vào mối quan hệ giữa cạnh và mặt).
Hướng Dẫn Giải Chi Tiết:
-
Chứng minh:
- Gọi
blà số mặt của khối đa diện. - Gọi
alà số cạnh của khối đa diện. - Theo giả thiết, tất cả các mặt của khối đa diện đều là tam giác. Mỗi mặt tam giác có 3 cạnh.
- Khi ta đếm tổng số cạnh của tất cả các mặt, ta sẽ có
3 times bcạnh. - Tuy nhiên, mỗi cạnh của khối đa diện lại là cạnh chung của đúng hai mặt. Điều này có nghĩa là khi ta cộng số cạnh của từng mặt, mỗi cạnh của khối đa diện đã được đếm hai lần.
- Do đó, ta có mối quan hệ:
3 times b = 2 times a. - Từ phương trình
3b = 2a, ta thấy rằng3bphải là một số chẵn (vì nó bằng2a). - Vì
3là số lẻ, để3blà số chẵn thìb(số mặt) phải là một số chẵn. - Vậy, một đa diện có các mặt là những tam giác thì tổng số các mặt của nó phải là một số chẵn.
- Gọi
-
Ví dụ:
- Xét hình tứ diện đều.
- Hình tứ diện đều có 4 mặt, và mỗi mặt là một tam giác đều.
- Số mặt
b = 4, đây là một số chẵn, phù hợp với kết luận đã chứng minh. - Hình tứ diện đều có 6 cạnh và 4 đỉnh. Ta kiểm tra lại công thức
3b = 2a:3 times 4 = 12và2 times 6 = 12. Mối quan hệ này đúng.
Mẹo Kiểm Tra: Luôn nhớ rằng khi đếm các yếu tố (cạnh, đỉnh, mặt) theo cách khác nhau, chúng ta sẽ có các mối quan hệ khác nhau. Ở đây, việc đếm cạnh theo mặt và đếm theo cạnh của khối đa diện là chìa khóa.
Lỗi Hay Gặp: Nhầm lẫn trong việc đếm số lần xuất hiện của mỗi cạnh, hoặc không suy luận được tính chẵn/lẻ từ phương trình 3b = 2a.

Đề Bài: Khối Đa Diện Lồi Và Khối Đa Diện Đều
Câu hỏi Toán 12 Hình học Bài 2 trang 15: Tìm ví dụ về khối đa diện lồi và khối đa diện không lồi trong thực tế.
Phân Tích Yêu Cầu:
Yêu cầu này đòi hỏi chúng ta liên hệ kiến thức toán học với thế giới thực, tìm các vật thể quen thuộc có hình dạng là khối đa diện lồi hoặc không lồi.
Kiến Thức/Nền Tảng Cần Dùng:
- Khối đa diện lồi: Là khối đa diện mà với hai điểm bất kỳ thuộc khối đa diện, đoạn thẳng nối hai điểm đó luôn nằm trọn trong khối đa diện đó. Hoặc, mọi mặt phẳng đi qua một mặt của khối đa diện đều có thể tách khối đa diện đó ra khỏi phần còn lại của không gian.
- Khối đa diện không lồi: Là khối đa diện không thỏa mãn các tính chất của khối đa diện lồi. Thường có “lõm” vào bên trong.
Hướng Dẫn Giải Chi Tiết:
-
Ví dụ về khối đa diện lồi trong thực tế:
- Kim tự tháp Ai Cập: Có đáy là hình vuông và các mặt bên là tam giác, đỉnh chóp nhọn. Mọi mặt phẳng đi qua một mặt của kim tự tháp đều có thể tách nó ra khỏi không gian.
- Viên kim cương (đã cắt): Nhiều viên kim cương được cắt theo các mặt phẳng tạo thành các khối đa diện lồi với nhiều mặt.
- Khối Rubik: Là một ví dụ điển hình của khối lập phương (một loại khối đa diện lồi).
- Hộp quà hình hộp chữ nhật: Một vật dụng quen thuộc, luôn là khối đa diện lồi.
-
Ví dụ về khối đa diện không lồi trong thực tế:
- Cái bàn: Một số loại bàn có chân bàn hoặc các bộ phận cấu thành tạo ra các “lõm” hoặc các phần không thể nhìn thấy toàn bộ từ một phía, làm cho tổng thể không phải là khối đa diện lồi. (Lưu ý: Đây là một ví dụ có thể gây tranh cãi tùy thuộc vào cách định nghĩa chi tiết của “cái bàn”, nhưng thường được dùng để minh họa cho sự không lồi).
- Một số đồ trang sức có hình dạng phức tạp: Có thể có các phần lồi và lõm xen kẽ.
- Các cấu trúc kiến trúc phức tạp: Một số tòa nhà có thiết kế “lạ” có thể tạo thành khối đa diện không lồi.
Mẹo Kiểm Tra: Hãy tưởng tượng bạn đang đi bộ bên trong vật thể đó. Nếu bạn có thể đi từ điểm này sang điểm kia mà không bao giờ đi ra ngoài hoặc gặp vật cản không mong muốn, thì nó có khả năng là khối đa diện lồi.
Lỗi Hay Gặp: Nhầm lẫn giữa khái niệm lồi/không lồi với các hình dạng phức tạp nói chung.
Câu hỏi Toán 12 Hình học Bài 2 trang 16: Đếm số đỉnh, số cạnh của khối bát diện đều.
Phân Tích Yêu Cầu:
Câu hỏi này yêu cầu xác định số đỉnh và số cạnh của một trong các khối đa diện đều.
Kiến Thức/Nền Tảng Cần Dùng:
- Khối bát diện đều: Là một trong năm khối đa diện đều (Platonic solids). Nó có 8 mặt, mỗi mặt là một tam giác đều, và tại mỗi đỉnh có 4 mặt gặp nhau.
Hướng Dẫn Giải Chi Tiết:
Khối bát diện đều có cấu trúc đặc trưng:
- Số đỉnh (V): Khối bát diện đều có 6 đỉnh. Hãy tưởng tượng nó giống như hai hình chóp tứ giác ghép đáy với nhau, đỉnh chóp trên và đỉnh chóp dưới, cùng với 4 đỉnh ở “xích đạo”.
- Số cạnh (E): Khối bát diện đều có 12 cạnh. Có 4 cạnh ở “đáy trên”, 4 cạnh ở “đáy dưới” và 4 cạnh nối từ đỉnh chóp trên xuống “xích đạo”, 4 cạnh nối từ đỉnh chóp dưới lên “xích đạo”. Tổng cộng 4+4+4 = 12 cạnh.
- Số mặt (F): Khối bát diện đều có 8 mặt (đúng như tên gọi), mỗi mặt là một tam giác đều.
Ta có thể kiểm tra lại bằng công thức Euler cho khối đa diện lồi: V - E + F = 2.
Với khối bát diện đều: 6 - 12 + 8 = 2. Công thức được thỏa mãn.
Mẹo Kiểm Tra: Hình dung khối bát diện đều như hai kim tự tháp tứ giác ghép đáy. Đếm đỉnh ở hai chóp và 4 đỉnh ở đáy chung. Đếm cạnh ở hai đáy và các cạnh nối từ đỉnh chóp xuống đáy.
Lỗi Hay Gặp: Nhầm lẫn số đỉnh, cạnh, mặt của các khối đa diện đều khác nhau (tứ diện, lập phương, bát diện, thập nhị diện, nhị thập diện).
Câu hỏi Toán 12 Hình học Bài 2 trang 17: Chứng minh rằng tam giác IEF, IFM, IMN, INE, JEF, JFM, JMN và JNE là những tam giác đều cạnh bằng a/2.
Phân Tích Yêu Cầu:
Bài toán này yêu cầu chứng minh các tam giác nhỏ được tạo ra từ các điểm trung điểm trong một tứ diện đều có cạnh bằng a là các tam giác đều có cạnh bằng a/2.
Kiến Thức/Nền Tảng Cần Dùng:
- Tứ diện đều: Là khối đa diện có 4 mặt là các tam giác đều bằng nhau, 4 đỉnh, 6 cạnh bằng nhau.
- Đường trung bình của tam giác: Đoạn thẳng nối trung điểm hai cạnh của tam giác thì song song với cạnh thứ ba và có độ dài bằng một nửa độ dài cạnh thứ ba đó.
Hướng Dẫn Giải Chi Tiết:
Giả sử ABCD là một tứ diện đều có cạnh bằng a. Điều này có nghĩa là AB = BC = CA = a (mặt đáy ABC là tam giác đều) và tương tự cho các mặt khác.
I, E, F lần lượt là trung điểm của các cạnh AC, AB, BC.
- Xét tam giác
ABC:Ilà trung điểmAC,Elà trung điểmAB. Do đó,IElà đường trung bình của tam giácABC.- Theo tính chất đường trung bình,
IEsong song vớiBCvàIE = 1/2 BC. VìBC = a, nênIE = a/2. - Tương tự,
IFlà đường trung bình của tam giácABC(nối trung điểmIcủaACvà trung điểmFcủaBC). Do đó,IF = 1/2 AB. VìAB = a, nênIF = a/2. EFlà đường trung bình của tam giácABC(nối trung điểmEcủaABvà trung điểmFcủaBC). Do đó,EF = 1/2 AC. VìAC = a, nênEF = a/2.- Vì
IE = IF = EF = a/2, tam giácIEFlà tam giác đều có cạnh bằnga/2.
Chứng minh tương tự cho các tam giác khác:
- Tam giác
IFM:Flà trung điểmBC,Mlà trung điểmCD.FMlà đường trung bình tam giácBCD.FM = 1/2 BD = a/2.Ilà trung điểmAC,Flà trung điểmBC.IF = 1/2 AB = a/2.IMlà đường trung bình tam giácACD.IM = 1/2 CD = a/2. VậyIFMđều cạnha/2. - Tam giác
IMN:Mlà trung điểmCD,Nlà trung điểmAD.MNlà đường trung bình tam giácACD.MN = 1/2 AC = a/2.Ilà trung điểmAC,Mlà trung điểmCD.IM = 1/2 AD = a/2.INlà đường trung bình tam giácACD.IN = 1/2 CD = a/2. VậyIMNđều cạnha/2. - Tam giác
INE:Nlà trung điểmAD,Elà trung điểmAB.NElà đường trung bình tam giácABD.NE = 1/2 BD = a/2.Ilà trung điểmAC,Nlà trung điểmAD.IN = 1/2 CD = a/2.Elà trung điểmAB,Ilà trung điểmAC.IE = 1/2 BC = a/2. VậyINEđều cạnha/2.
Các tam giác còn lại (JEF, JFM, JMN, JNE) liên quan đến đỉnh J (có thể là trung điểm của một cạnh khác hoặc một điểm tương ứng ở mặt trên). Nếu J cũng là một trung điểm tương ứng (ví dụ: trung điểm của A'B' nếu xét một hình lớn hơn), thì lập luận tương tự với các tam giác khác sẽ cho kết quả tương tự. Tuy nhiên, dựa trên hình 1.17, I, E, F, M, N có vẻ là trung điểm của các cạnh AC, AB, BC, CD, AD tương ứng. Nếu J là một đỉnh khác hoặc một trung điểm khác, ta cần thêm thông tin. Tuy nhiên, giả định phổ biến nhất cho bài toán này là các điểm I, E, F, M, N là trung điểm của các cạnh AC, AB, BC, CD, AD và J có thể là trung điểm của BD hoặc A'B' tùy thuộc vào hình vẽ cụ thể. Nếu J là trung điểm của BD, thì JE, JF, JM, JN cũng sẽ là đường trung bình của các tam giác tương ứng.
Với giả định I, E, F, M, N là trung điểm của AC, AB, BC, CD, AD và J là trung điểm của BD:
- Xét tam giác
ABD:Etrung điểmAB,Ntrung điểmAD.ENlà đường trung bình,EN = 1/2 BD = a/2. - Xét tam giác
BCD:Ftrung điểmBC,Mtrung điểmCD.FMlà đường trung bình,FM = 1/2 BD = a/2. - Xét tam giác
ACD:Itrung điểmAC,Mtrung điểmCD.IMlà đường trung bình,IM = 1/2 AD = a/2. - Xét tam giác
ABC:Itrung điểmAC,Etrung điểmAB.IE = 1/2 BC = a/2.
Nếu J là trung điểm của BD:
- Xét tam giác
ABD:Etrung điểmAB,Jtrung điểmBD.EJlà đường trung bình,EJ = 1/2 AD = a/2. - Xét tam giác
CBD:Ftrung điểmBC,Jtrung điểmBD.FJlà đường trung bình,FJ = 1/2 CD = a/2. - Xét tam giác
ACD:Mtrung điểmCD,Ntrung điểmAD.MN = 1/2 AC = a/2. - Xét tam giác
BCD:Ftrung điểmBC,Mtrung điểmCD.FM = 1/2 BD = a/2.
Trong trường hợp này, các tam giác IEF, IFM, IMN, INE đã được chứng minh là đều cạnh a/2. Nếu J là trung điểm của BD, thì các tam giác JEF, JFM, JMN, JNE cũng sẽ có các cạnh là đường trung bình của các tam giác lớn, và do đó có độ dài a/2. Ví dụ, JEF: JE = a/2 (đường trung bình tam giác ABD), JF = a/2 (đường trung bình tam giác BCD), EF = a/2 (đường trung bình tam giác ABC). Vậy JEF là tam giác đều cạnh a/2.
Mẹo Kiểm Tra: Luôn vẽ hình ra và đánh dấu các điểm trung điểm. Sau đó, xác định các tam giác mà các đoạn thẳng nối trung điểm tạo thành đường trung bình.
Lỗi Hay Gặp: Nhầm lẫn các cạnh của tứ diện, hoặc áp dụng sai tính chất đường trung bình.
Câu hỏi Toán 12 Hình học Bài 2 trang 18: Chứng minh rằng AB’CD’.A’B’C’D’ có cạnh bằng a (h.1.22b).
Phân Tích Yêu Cầu:
Câu hỏi này yêu cầu chứng minh một hình tứ diện cụ thể, được tạo thành từ các đỉnh của hình lập phương, có các cạnh bằng nhau và bằng cạnh của hình lập phương. Tuy nhiên, đề bài có vẻ có lỗi đánh máy khi nói “AB’CD’.A’B’C’D’ có cạnh bằng a”. Hình AB’CD’ là một tứ diện, còn A’B’C’D’ là một mặt của hình lập phương. Giả định câu hỏi muốn hỏi về tứ diện AB’CD’.
Kiến Thức/Nền Tảng Cần Dùng:
- Hình lập phương: Có 6 mặt là hình vuông bằng nhau, 12 cạnh bằng nhau, 8 đỉnh.
- Đường chéo mặt: Trong hình vuông cạnh
a, đường chéo mặt có độ dàiasqrt{2}. - Tứ diện đều: Là tứ diện có 4 mặt là tam giác đều, 6 cạnh bằng nhau.
Hướng Dẫn Giải Chi Tiết:
Giả sử ABCD.A’B’C’D’ là hình lập phương có cạnh bằng a.
Chúng ta cần xem xét tứ diện AB’CD’. Các cạnh của tứ diện này là: AB', AC', AD', B’C', B’D', C’D’.
-
Các cạnh
AB',AC',AD'là các đường chéo của các mặt hình vuông của hình lập phương.- Mặt
ABB’A’là hình vuông cạnha, nên đường chéoAB'có độ dàisqrt{a^2 + a^2} = asqrt{2}. - Mặt
ACC’A’là hình vuông cạnha, nên đường chéoAC'có độ dàisqrt{a^2 + a^2} = asqrt{2}. - Mặt
ADD’A’là hình vuông cạnha, nên đường chéoAD'có độ dàisqrt{a^2 + a^2} = asqrt{2}.
- Mặt
-
Các cạnh
B’C',B’D',C’D’là các cạnh của mặt đáyA’B’C’D’hoặc các đường chéo của các mặt bên.B’C'là cạnh của hình vuôngA’B’C’D', nênB’C' = a.C’D'là cạnh của hình vuôngA’B’C’D', nênC’D' = a.B’D'là đường chéo của hình vuôngA’B’C’D', nênB’D' = asqrt{2}.
Từ kết quả trên, ta thấy các cạnh của tứ diện AB’CD’ không bằng nhau (asqrt{2}, asqrt{2}, asqrt{2}, a, a, asqrt{2}). Do đó, tứ diện AB’CD’ không phải là tứ diện đều và các cạnh của nó không chỉ bằng a.
Phân Tích Lại Đề Bài:
Có khả năng đề bài gốc có lỗi hoặc đang đề cập đến một hình khác. Nếu đề bài muốn nói về tứ diện tạo bởi các đỉnh của hình lập phương mà các cạnh của nó là đường chéo của các mặt, thì đó là tứ diện AB’C’D hoặc các tứ diện tương tự.
Ví dụ: xét tứ diện AB’C’D.
AB'là đường chéo mặtABB’A', dàiasqrt{2}.AC’là đường chéo mặtACC’A', dàiasqrt{2}.ADlà cạnh của hình lập phương, dàia.B’C’là cạnh của hình lập phương, dàia.B’Dlà đường chéo mặtA’BDD’, dàiasqrt{2}.C’Dlà đường chéo mặtCDD’C’, dàiasqrt{2}.
Các cạnh này cũng không bằng nhau.
Khả năng khác: Đề bài có thể muốn nói về một hình khác được tạo ra từ hình lập phương. Tuy nhiên, với thông tin hiện có, việc chứng minh “AB’CD’ có cạnh bằng a” là không đúng. Nếu đề bài muốn nói “tứ diện có các cạnh bằng đường chéo mặt của hình lập phương cạnh a”, thì đó là tứ diện AB’C’D hoặc A’BC’D… và các cạnh này có độ dài asqrt{2}.
Kết luận dựa trên đề bài gốc:
Dựa trên đề bài “Chứng minh rằng AB’CD’.A’B’C’D’ có cạnh bằng a (h.1.22b)”, và giả định nó đề cập đến tứ diện AB’CD’ và hình lập phương ABCD.A’B’C’D’ cạnh a:
Các cạnh của tứ diện AB’CD’ bao gồm các đường chéo mặt (AB', AC', AD') có độ dài asqrt{2} và các cạnh của mặt đáy (B’C', C’D') có độ dài a, cùng đường chéo mặt B’D' có độ dài asqrt{2}.
Do đó, không phải tất cả các cạnh của tứ diện AB’CD’ đều bằng a. Chỉ có các cạnh là cạnh của hình vuông đáy (B’C', C’D', D’A', A’B') mới có độ dài a. Các cạnh còn lại là đường chéo mặt có độ dài asqrt{2}.
Vì vậy, không thể chứng minh rằng tứ diện AB’CD’ có cạnh bằng a.
Lỗi Hay Gặp: Lỗi đánh máy trong đề bài, hoặc hiểu sai hình dạng cần chứng minh.
Bài 1 (trang 18 SGK Hình học 12): Cắt bìa theo mẫu dưới đây (h.123), gấp theo đường kẻ, rồi dán các mép lại để được các hình tứ diện đều, hình lập phương và hình bát diện đều.
Phân Tích Yêu Cầu:
Bài tập này mang tính thực hành, yêu cầu học sinh tự tạo ra các khối đa diện đều từ các mẫu giấy. Không có yêu cầu chứng minh hay tính toán phức tạp, chủ yếu là rèn luyện kỹ năng hình dung không gian và sự khéo léo.
Kiến Thức/Nền Tảng Cần Dùng:
- Biết hình dạng của các khối đa diện đều: tứ diện đều, lập phương, bát diện đều.
- Khả năng đọc và làm theo hướng dẫn từ hình vẽ (mẫu cắt).
Hướng Dẫn Giải Chi Tiết:
Bài tập này không yêu cầu lời giải bằng văn bản mà là một hoạt động thực hành. Để hoàn thành bài tập này, học sinh cần:
- Tìm mẫu cắt: Tìm hình 1.23 trong Sách Giáo Khoa Hình học 12. Hình này sẽ cung cấp các mẫu giấy có các đường kẻ (để gấp) và các đường cắt.
- Cắt bìa: Cẩn thận cắt theo các
Ngày chỉnh sửa nội dung mới nhất Tháng 1 16, 2026 by Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.