Giải Toán Lớp 5 Trang 116 Kết Nối Tri Thức: Chinh Phục Bài Tập Hình Học và Chu Vi

by Thầy Đông · January 6, 2026

Rate this post

Trang 116 của sách giáo khoa Toán lớp 5 thuộc bộ Kết nối tri thức tập trung vào các bài luyện tập chung, đòi hỏi học sinh phải áp dụng kiến thức về diện tích hình tam giác, chu vi và diện tích hình tròn. Để giúp các em nắm vững và tự tin giải quyết các dạng bài này, bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu, kèm theo phân tích sâu sắc từng bước làm, các mẹo kiểm tra và những lỗi sai thường gặp. Mục tiêu là trang bị cho học sinh không chỉ đáp án mà còn là phương pháp tư duy toán học hiệu quả, giúp các em chủ động chinh phục giải toán lớp 5 trang 116.

Đề Bài

Bài 1:
a) Vẽ vào vở các hình tam giác sau và vẽ đường cao lần lượt ứng với đáy BC, EG và IK của mỗi hình tam giác đó.
b) Tính diện tích các hình tam giác ở câu a trong trường hợp mỗi ô vuông có cạnh 2,5 cm.

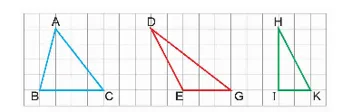Hình minh họa các tam giác và đường cao

Bài 2:
Chọn câu trả lời đúng. Trong hình bên, biết hình tròn bé nhất có bán kính 50 cm, hình tròn lớn nhất có bán kính 200 cm.

a) Đường kính mỗi hình tròn màu xanh lá cây là:
A. 100 cm
B. 150 cm
C. 400 cm
D. 300 cm

b) Chu vi hình tròn lớn nhất gấp mấy lần chu vi hình tròn bé nhất?
A. 2 lần
B. 3 lần
C. 4 lần
D. 5 lần

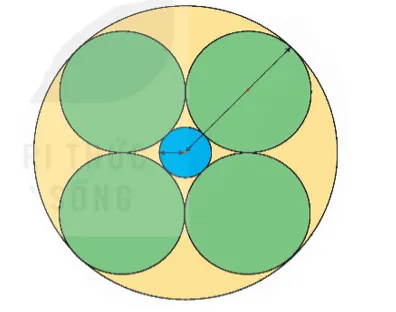Hình minh họa các hình tròn với kích thước khác nhau

Bài 3:
Một cái ao dạng nửa hình tròn có kích thước như hình vẽ. Tính chu vi cái ao.

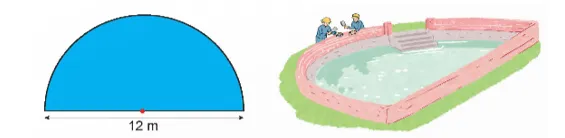Hình minh họa cái ao dạng nửa hình tròn

Phân Tích Yêu Cầu và Kiến Thức Cần Dùng

Các bài tập trong phần giải toán lớp 5 trang 116 đòi hỏi sự kết hợp nhuần nhuyễn giữa lý thuyết và thực hành. Chúng ta cần ôn lại các khái niệm và công thức sau:

Bài 1: Diện tích tam giác và đường cao

Đường cao của tam giác: Là đoạn thẳng kẻ từ một đỉnh của tam giác, vuông góc với cạnh đối diện (hoặc đường thẳng chứa cạnh đối diện).
Công thức tính diện tích tam giác: Diện tích tam giác bằng nửa tích của cạnh đáy với chiều cao tương ứng.
\text{Diện tích} = \frac{1}{2} \times \text{đáy} \times \text{chiều cao}
Hoặc công thức thu gọn:
S = \frac{1}{2} \times a \times h_a
trong đó:
- S là diện tích.
- a là độ dài cạnh đáy.
- h_a là độ dài đường cao tương ứng với đáy a.

Để giải bài này, chúng ta cần xác định đúng đáy và vẽ đường cao tương ứng cho từng loại tam giác (nhọn, tù, vuông). Sau đó, dựa vào lưới ô vuông để đo đạc các cạnh đáy và chiều cao, áp dụng công thức tính diện tích.

Bài 2: Đường kính, bán kính và chu vi hình tròn

Bán kính (r): Khoảng cách từ tâm hình tròn đến một điểm bất kỳ trên đường tròn.
Đường kính (d): Đoạn thẳng đi qua tâm, nối hai điểm trên đường tròn. Đường kính bằng hai lần bán kính:
$d = 2 \times r$
Chu vi hình tròn (C): Độ dài đường bao quanh hình tròn.
- Sử dụng đường kính:
  $C = d \times 3,14$
- Sử dụng bán kính:
  $C = r \times 2 \times 3,14$
  Trong đó, 3,14 là giá trị gần đúng của số Pi (pi).

Ở bài này, chúng ta cần hiểu rõ mối quan hệ giữa bán kính và đường kính, cũng như cách chu vi của hai hình tròn liên quan với nhau khi bán kính của chúng thay đổi.

Bài 3: Chu vi nửa hình tròn

Nửa chu vi hình tròn: Bằng một nửa chu vi của hình tròn đầy đủ.
$\text{Nửa chu vi} = \frac{1}{2} \times d \times 3,14$
Chu vi cái ao (dạng nửa hình tròn): Bao gồm nửa chu vi của đường tròn và đường kính của nó (là phần đáy của nửa hình tròn).
$\text{Chu vi ao} = (\frac{1}{2} \times d \times 3,14) + d$
Hoặc:
$\text{Chu vi ao} = (\frac{1}{2} \times 2 \times r \times 3,14) + 2 \times r$
$\text{Chu vi ao} = (r \times 3,14) + 2 \times r$

Chúng ta cần xác định đúng các yếu tố cấu thành nên chu vi của cái ao.

Hướng Dẫn Giải Chi Tiết

Bài 1: Vẽ đường cao và tính diện tích tam giác

a) Vẽ đường cao:

Tam giác ABC:
- Đáy BC: Kẻ đường cao từ đỉnh A vuông góc với đường thẳng BC. Gọi chân đường cao là H. Đoạn AH là đường cao tương ứng với đáy BC.
Tam giác EFG:
- Đáy EG: Kẻ đường cao từ đỉnh F vuông góc với đường thẳng EG. Gọi chân đường cao là K. Đoạn FK là đường cao tương ứng với đáy EG.
Tam giác HIK:
- Đáy IK: Kẻ đường cao từ đỉnh H vuông góc với đường thẳng IK. Gọi chân đường cao là L. Đoạn HL là đường cao tương ứng với đáy IK.

Lưu ý: Với các tam giác có góc tù, đường cao có thể nằm ngoài tam giác. Với tam giác vuông, hai cạnh góc vuông có thể đồng thời là đường cao và cạnh đáy.

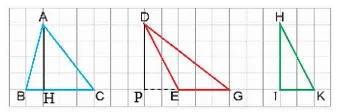Minh họa đường cao trong các tam giác

b) Tính diện tích các hình tam giác:

Để tính diện tích, chúng ta cần xác định độ dài đáy và chiều cao dựa vào lưới ô vuông. Giả sử mỗi ô vuông có cạnh 2,5 cm.

Tam giác ABC:
- Đáy BC: Đếm số ô vuông theo chiều ngang của BC. Giả sử BC có độ dài là x ô vuông. Chiều dài thực tế của BC là: $a_{BC} = x \times 2,5 \text{cm}$ .
- Chiều cao AH: Đếm số ô vuông theo chiều dọc từ A xuống BC. Giả sử AH có độ dài là h ô vuông. Chiều cao thực tế của AH là: $h_a = h \times 2,5 \text{cm}$ .
- Diện tích tam giác ABC:
 $S{ABC} = \frac{1}{2} \times a{BC} \times h_a = \frac{1}{2} \times (x \times 2,5) \times (h \times 2,5) \text{cm}^2$
Tam giác EFG:
- Đáy EG: Tương tự, đếm số ô vuông, giả sử là y ô. Chiều dài thực tế của EG là: $a_{EG} = y \times 2,5 \text{cm}$ .
- Chiều cao FK: Đếm số ô vuông, giả sử là k ô. Chiều cao thực tế của FK là: $h_f = k \times 2,5 \text{cm}$ .
- Diện tích tam giác EFG:
 $S{EFG} = \frac{1}{2} \times a{EG} \times h_f = \frac{1}{2} \times (y \times 2,5) \times (k \times 2,5) \text{cm}^2$
Tam giác HIK:
- Đáy IK: Đếm số ô vuông, giả sử là z ô. Chiều dài thực tế của IK là: $a_{IK} = z \times 2,5 \text{cm}$ .
- Chiều cao HL: Đếm số ô vuông, giả sử là l ô. Chiều cao thực tế của HL là: $h_h = l \times 2,5 \text{cm}$ .
- Diện tích tam giác HIK:
 $S{HIK} = \frac{1}{2} \times a{IK} \times h_h = \frac{1}{2} \times (z \times 2,5) \times (l \times 2,5) \text{cm}^2$

Ví dụ cụ thể dựa trên hình ảnh:
Trong hình vẽ, có thể ước lượng số ô vuông như sau (lưu ý đây là ước lượng dựa trên hình ảnh, cần đếm chính xác trên vở của học sinh):

Tam giác ABC: Giả sử đáy BC là 4 ô, chiều cao AH là 3 ô.
- Đáy BC: $4 \times 2,5 = 10 \text{cm}$
- Chiều cao AH: $3 \times 2,5 = 7,5 \text{cm}$
- Diện tích: $\frac{1}{2} \times 10 \times 7,5 = 37,5 \text{cm}^2$
Tam giác EFG: Giả sử đáy EG là 6 ô, chiều cao FK là 4 ô.
- Đáy EG: $6 \times 2,5 = 15 \text{cm}$
- Chiều cao FK: $4 \times 2,5 = 10 \text{cm}$
- Diện tích: $\frac{1}{2} \times 15 \times 10 = 75 \text{cm}^2$
Tam giác HIK: Giả sử đáy IK là 5 ô, chiều cao HL là 5 ô.
- Đáy IK: $5 \times 2,5 = 12,5 \text{cm}$
- Chiều cao HL: $5 \times 2,5 = 12,5 \text{cm}$
- Diện tích: $\frac{1}{2} \times 12,5 \times 12,5 = 78,125 \text{cm}^2$

Mẹo kiểm tra: Đảm bảo rằng bạn đã vẽ đường cao vuông góc với cạnh đáy hoặc đường thẳng chứa cạnh đáy. Khi tính diện tích, kiểm tra lại việc đếm ô vuông và phép tính nhân chia.

Lỗi hay gặp:

Vẽ đường cao không vuông góc với đáy.
Nhầm lẫn giữa cạnh đáy và chiều cao.
Quên chia đôi kết quả khi áp dụng công thức diện tích tam giác.
Tính toán sai khi nhân với 2,5 hoặc khi làm việc với số thập phân.

Bài 2: Chu vi và đường kính hình tròn

a) Đường kính mỗi hình tròn màu xanh lá cây:

Phân tích: Hình tròn màu xanh lá cây nằm giữa hình tròn bé nhất và hình tròn lớn nhất. Phần “chênh lệch” bán kính giữa hình tròn lớn nhất và hình tròn bé nhất chính là bán kính của hình tròn xanh lá cây. Tuy nhiên, câu hỏi hỏi về đường kính của hình tròn màu xanh lá cây, có thể hiểu là hình tròn nằm giữa hai hình có bán kính cho trước. Dựa vào hình ảnh, hình tròn màu xanh lá cây có vẻ như là một “vành đai” hoặc là một hình tròn nằm giữa hai hình tròn đồng tâm. Nếu hiểu “hình tròn màu xanh lá cây” là một hình tròn riêng biệt được vẽ giữa hai hình tròn kia, và bán kính của nó bằng hiệu bán kính của hai hình tròn lớn và nhỏ:
- Bán kính hình tròn lớn nhất: $R = 200 \text{cm}$
- Bán kính hình tròn bé nhất: $r = 50 \text{cm}$
- Nếu “hình tròn màu xanh lá cây” có bán kính là sự chênh lệch hoặc một giá trị nằm giữa: Dựa vào hình ảnh, có vẻ hình tròn màu xanh lá cây có đường kính là hiệu của hai bán kính, hoặc bằng bán kính hình tròn lớn trừ bán kính hình tròn bé để tạo thành một “vành đai” có chiều rộng bằng bán kính ban đầu của nó. Tuy nhiên, nếu hiểu câu hỏi là “đường kính của một hình tròn có bán kính bằng hiệu hai bán kính cho trước”, thì:
- Bán kính hình tròn xanh lá cây = $200 \text{cm} - 50 \text{cm} = 150 \text{cm}$ .
- Đường kính hình tròn xanh lá cây = $2 \times 150 \text{cm} = 300 \text{cm}$ .
Nếu cách hiểu trên là đúng, thì đáp án D. 300 cm là phù hợp.
Tuy nhiên, nếu hình tròn màu xanh lá cây là một trong hai hình được tô màu xanh lá cây trong hình vẽ, và chúng được vẽ bên trong hình tròn lớn và ngoài hình tròn bé, thì câu hỏi có thể ám chỉ đến đường kính của một hình tròn có bán kính bằng 150cm.
Dựa vào cách trình bày “Đường kính mỗi hình tròn màu xanh lá cây là”, và các đáp án, khả năng cao là chúng ta đang xét một hình tròn có bán kính $150 \text{cm}$ .
- Bán kính hình tròn màu xanh lá cây: $r_{xanh} = 150 \text{cm}$ .
- Đường kính hình tròn màu xanh lá cây: $d{xanh} = 2 \times r{xanh} = 2 \times 150 \text{cm} = 300 \text{cm}$ .
 -> Đáp án D. 300 cm là hợp lý.
Kiểm tra lại cách hiểu: Hình tròn bé nhất có bán kính 50cm, đường kính 100cm. Hình tròn lớn nhất có bán kính 200cm, đường kính 400cm. Khoảng trống giữa chúng có chiều rộng 150cm (là bán kính của hình tròn xanh lá cây). Nếu đường kính hình tròn xanh lá cây là 300cm thì bán kính là 150cm. Vậy đáp án D là chính xác.

b) Chu vi hình tròn lớn nhất gấp mấy lần chu vi hình tròn bé nhất?

Phân tích: Chúng ta cần tính chu vi của cả hai hình tròn rồi so sánh.
Hình tròn bé nhất:
- Bán kính: $r_{bé} = 50 \text{cm}$
- Chu vi: $C{bé} = r{bé} \times 2 \times 3,14 = 50 \times 2 \times 3,14 = 100 \times 3,14 = 314 \text{cm}$ .
Hình tròn lớn nhất:
- Bán kính: $r_{lớn} = 200 \text{cm}$
- Chu vi: $C{lớn} = r{lớn} \times 2 \times 3,14 = 200 \times 2 \times 3,14 = 400 \times 3,14 = 1256 \text{cm}$ .
So sánh chu vi:
- Số lần chu vi lớn gấp chu vi bé là: $C{lớn} : C{bé} = 1256 : 314 = 4$ (lần).
Hoặc cách giải nhanh hơn: Tỷ lệ chu vi của hai hình tròn bằng tỷ lệ bán kính (hoặc đường kính) của chúng.
- Tỷ lệ bán kính: $r{lớn} : r{bé} = 200 : 50 = 4$ (lần).
- Do đó, chu vi hình tròn lớn nhất gấp chu vi hình tròn bé nhất 4 lần.
-> Đáp án C. 4 lần là chính xác.

Mẹo kiểm tra:

Đối với câu a, hãy vẽ hình ra giấy nháp để hình dung rõ hơn về vị trí và kích thước của hình tròn màu xanh. Đảm bảo bạn đã cộng hoặc trừ bán kính một cách chính xác.
Đối với câu b, sau khi tính chu vi, hãy thử rút gọn phép tính bằng cách chia bán kính hoặc đường kính trước, sau đó nhân với $2 \times 3,14$ để thấy rõ mối quan hệ tỷ lệ.

Lỗi hay gặp:

Nhầm lẫn giữa bán kính và đường kính.
Tính chu vi theo công thức diện tích hoặc ngược lại.
Sử dụng sai số $\pi$ (nếu đề bài yêu cầu dùng giá trị khác 3,14).
Nhầm lẫn số lần gấp khi so sánh chu vi, chỉ tính ra hiệu số thay vì thương số.

Bài 3: Chu vi cái ao dạng nửa hình tròn

Phân tích: Cái ao có dạng nửa hình tròn. Chu vi của nó bao gồm:
1. Đường cong của nửa hình tròn.
2. Đoạn thẳng là đường kính của nửa hình tròn đó.
Đề bài cho: Hình vẽ cho thấy cái ao có đường kính là 12 m.
- Đường kính: $d = 12 \text{m}$ .
- Bán kính: $r = d : 2 = 12 : 2 = 6 \text{m}$ .
Tính chu vi:
1. Tính chu vi của cả hình tròn có đường kính 12 m:
  $C_{tròn} = d \times 3,14 = 12 \times 3,14 = 37,68 \text{m}$ .
2. Tính độ dài đường cong của nửa hình tròn (nửa chu vi):
  $\text{Nửa chu vi} = C_{tròn} : 2 = 37,68 : 2 = 18,84 \text{m}$ .
3. Tính chu vi cái ao bằng cách cộng nửa chu vi và đường kính:
  $\text{Chu vi ao} = \text{Nửa chu vi} + d = 18,84 \text{m} + 12 \text{m} = 30,84 \text{m}$ .
Kiểm tra lại lời giải trong bài gốc: Lời giải trong bài gốc ghi “Chu vi cái ao là: 37,68 : 2 = 18,84 (m)”. Điều này chỉ tính nửa chu vi của hình tròn, chưa cộng thêm đường kính. Đây là một lỗi sai phổ biến. Chu vi của cái ao PHẢI bao gồm cả phần đường thẳng nối hai đầu của nửa hình tròn.
Lời giải đúng phải là:
- Bán kính cái ao: $12 : 2 = 6 \text{m}$
- Nửa chu vi cái ao: $6 \times 2 \times 3,14 : 2 = 6 \times 3,14 = 18,84 \text{m}$
- Chu vi cái ao (bao gồm đường kính): $18,84 + 12 = 30,84 \text{m}$ .
Đáp số: 30,84 m.

Mẹo kiểm tra: Luôn nhớ rằng chu vi của một hình dạng kín là tổng độ dài tất cả các cạnh bao quanh nó. Đối với nửa hình tròn, đó là đường cong và đoạn thẳng đáy.

Lỗi hay gặp:

Chỉ tính nửa chu vi hình tròn mà quên cộng thêm đường kính.
Nhầm lẫn giữa bán kính và đường kính khi áp dụng công thức.
Tính toán sai với số thập phân 3,14.

Đáp Án/Kết Quả

Bài 1:
a) Vẽ các hình tam giác và đường cao tương ứng như hướng dẫn.
b) Diện tích các tam giác được tính dựa trên số ô vuông và cạnh ô vuông là 2,5 cm, áp dụng công thức $S = \frac{1}{2} \times \text{đáy} \times \text{chiều cao}$ . (Kết quả cụ thể phụ thuộc vào số ô vuông đếm được).

Bài 2:
a) Đường kính hình tròn màu xanh lá cây là: 300 cm (Đáp án D).
b) Chu vi hình tròn lớn nhất gấp chu vi hình tròn bé nhất: 4 lần (Đáp án C).

Bài 3:
Chu vi cái ao dạng nửa hình tròn là: 30,84 m.

Kết thúc bài giải toán lớp 5 trang 116 này, hy vọng rằng các em học sinh đã có cái nhìn rõ ràng hơn về cách giải các bài tập liên quan đến diện tích tam giác và chu vi hình tròn. Việc nắm vững công thức, hiểu rõ bản chất của từng đại lượng và rèn luyện kỹ năng áp dụng linh hoạt vào các bài toán thực tế sẽ giúp các em tự tin hơn trong học tập. Hãy luôn ghi nhớ các bước phân tích đề bài, xác định kiến thức cần dùng và thực hiện phép tính cẩn thận để đạt kết quả tốt nhất.

Ngày chỉnh sửa nội dung mới nhất January 6, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.