Bài 4 Trang 98 Toán 10 Tập 1 Cánh Diều: Tính Tích Vô Hướng Của Hai Vectơ
Chào mừng bạn đến với phần giải chi tiết Bài 4 trang 98 Toán 10 Tập 1 Cánh Diều. Bài viết này tập trung vào việc tính tích vô hướng của hai vectơ trong một hình vuông, cung cấp kiến thức nền tảng và phương pháp giải bài tập hiệu quả. Chúng ta sẽ cùng nhau phân tích yêu cầu, nắm vững các định lý liên quan và thực hiện từng bước giải một cách rõ ràng nhất.
Đề Bài
Cho hình vuông ABCD cạnh a. Tính các tích vô hướng sau:
a) AB→ . AC→;
b) AC→ . BD→.
Phân Tích Yêu Cầu
Bài toán yêu cầu tính tích vô hướng của hai cặp vectơ trong một hình vuông có cạnh là a. Cụ thể, chúng ta cần xác định giá trị của AB→ . AC→ và AC→ . BD→. Để giải quyết bài toán này, chúng ta cần vận dụng các kiến thức về hình vuông, các định lý liên quan đến tích vô hướng của hai vectơ và quy tắc tính toán.
Kiến Thức/Nền Tảng Cần Dùng
Để giải quyết bài toán này, chúng ta cần nhớ lại các kiến thức sau:
- Định nghĩa tích vô hướng: Tích vô hướng của hai vectơ
u→vàv→được định nghĩa làu→ . v→ = |u→| . |v→| . cos(u→, v→), trong đó|u→|và|v→|là độ dài của hai vectơ, và(u→, v→)là góc tạo bởi hai vectơ đó. - Tính chất của hình vuông:
- Các cạnh bằng nhau:
AB = BC = CD = DA = a. - Các góc bằng 90 độ:
∠BAD = ∠ABC = ∠BCD = ∠CDA = 90°. - Hai đường chéo bằng nhau và vuông góc với nhau:
AC = BDvàAC ⊥ BD. - Đường chéo là tia phân giác của các góc tại đỉnh. Ví dụ,
AClà tia phân giác của∠BAD, nên∠BAC = ∠CAD = 45°.
- Các cạnh bằng nhau:
- Định lý Pytago: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông. Áp dụng cho tam giác
ABCvuông tạiB, ta cóAC² = AB² + BC².
Hướng Dẫn Giải Chi Tiết
Chúng ta sẽ lần lượt giải quyết từng phần của bài toán:
a) Tính AB→ . AC→
Theo định nghĩa tích vô hướng, ta có:AB→ . AC→ = AB . AC . cos(AB→, AC→)
Trước hết, chúng ta cần xác định độ dài của các cạnh và đường chéo, cũng như góc giữa hai vectơ AB→ và AC→.
- Độ dài cạnh AB:
AB = a(theo giả thiết đề bài). - Độ dài đường chéo AC: Xét tam giác
ABCvuông tạiB. Áp dụng định lý Pytago, ta có:AC² = AB² + BC²AC² = a² + a²AC² = 2a²AC = sqrt{2a²} = asqrt{2} - Góc giữa AB→ và AC→: Trong hình vuông
ABCD, đường chéoAClà tia phân giác của góc∠BAD. Do đó, góc∠BACbằng một nửa góc vuông:∠BAC = frac{1}{2} ∠BAD = frac{1}{2} times 90° = 45°
Góc giữa hai vectơAB→vàAC→chính là góc∠BAC.
Bây giờ, ta thay các giá trị vào công thức tính tích vô hướng:AB→ . AC→ = AB . AC . cos(∠BAC)AB→ . AC→ = a . (asqrt{2}) . cos(45°)
Ta biết cos(45°) = frac{sqrt{2}}{2}.AB→ . AC→ = a . asqrt{2} . frac{sqrt{2}}{2}AB→ . AC→ = a² . (sqrt{2} times frac{sqrt{2}}{2})AB→ . AC→ = a² . (frac{2}{2})AB→ . AC→ = a² . 1AB→ . AC→ = a²
Mẹo kiểm tra: Ta có thể kiểm tra bằng cách phân tích vectơ. Đặt A là gốc tọa độ. Nếu A = (0,0), B = (a,0), D = (0,a), C = (a,a).
Khi đó, AB→ = (a,0) và AC→ = (a,a).
Tích vô hướng: AB→ . AC→ = aa + 0a = a². Kết quả khớp.
Lỗi hay gặp:
- Tính sai độ dài đường chéo
AC. - Nhầm lẫn góc giữa hai vectơ hoặc giá trị cosin của góc đó.
- Thực hiện phép nhân các đại lượng không chính xác.
b) Tính AC→ . BD→
Trong hình vuông ABCD, hai đường chéo AC và BD có các tính chất quan trọng:
- Chúng bằng nhau (
AC = BD). - Chúng vuông góc với nhau (
AC ⊥ BD).
Vì hai vectơ AC→ và BD→ vuông góc với nhau, góc giữa chúng là 90°.
Theo định nghĩa tích vô hướng:AC→ . BD→ = |AC→| . |BD→| . cos(AC→, BD→)AC→ . BD→ = AC . BD . cos(90°)
Ta biết cos(90°) = 0.AC→ . BD→ = AC . BD . 0AC→ . BD→ = 0
Mẹo kiểm tra: Khi hai vectơ vuông góc với nhau, tích vô hướng của chúng luôn bằng 0. Điều này là một định lý cơ bản trong tích vô hướng.
Lỗi hay gặp:
- Quên mất tính chất hai đường chéo vuông góc của hình vuông.
- Áp dụng sai công thức tích vô hướng khi góc là 90 độ.
Đáp Án/Kết Quả
Sau khi phân tích và thực hiện các bước tính toán chi tiết, chúng ta có kết quả cho bài toán:
a) AB→ . AC→ = a²
b) AC→ . BD→ = 0
Hình Ảnh Minh Họa
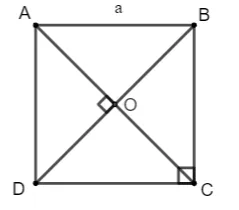 Hình vuông ABCD với các đường chéoHình 1: Minh họa hình vuông ABCD và các vectơ liên quan.
Hình vuông ABCD với các đường chéoHình 1: Minh họa hình vuông ABCD và các vectơ liên quan.
Kết Luận
Bài toán Bài 4 trang 98 Toán 10 Tập 1 Cánh Diều đã được giải quyết một cách chi tiết, làm rõ cách áp dụng định nghĩa tích vô hướng và các tính chất của hình vuông. Việc nắm vững các kiến thức nền tảng này không chỉ giúp bạn hoàn thành bài tập mà còn xây dựng nền tảng vững chắc cho việc giải các bài toán phức tạp hơn về vectơ và hình học trong chương trình Toán học lớp 10.
Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.













