Định Lý Ba Đường Vuông Góc: Khái Niệm, Chứng Minh Và Ứng Dụng Trong Toán Học

by Thầy Đông · January 7, 2026

Rate this post

Định lý ba đường vuông góc đóng vai trò là một khái niệm nền tảng trong chương trình hình học không gian, giúp xây dựng cầu nối vững chắc giữa các đối tượng hình học phẳng và không gian. Hiểu rõ định lý này không chỉ giúp giải quyết các bài toán phức tạp mà còn là chìa khóa để nắm bắt sâu sắc hơn các quy luật hình thành và phát triển trong tư duy toán học.

Đề Bài

<?xml encoding=”utf-8″ ?><?xml encoding=”utf-8″ ?> Định lý 3 đường vuông góc là gì? Phương pháp chứng minh Định lý ba đường vuông góc? Nhận biết khái niệm đường vuông góc là yêu cầu cần đạt trong chương trình toán lớp mấy? Định hướng phương pháp hình thành và phát triển các phẩm chất chủ yếu và năng lực chung môn toán?

Phân Tích Yêu Cầu

Bài viết này tập trung làm rõ định nghĩa, phương pháp chứng minh của Định lý 3 đường vuông góc. Đồng thời, bài viết sẽ xác định rõ cấp lớp học mà khái niệm đường vuông góc được yêu cầu nhận biết, và cung cấp định hướng về phương pháp giáo dục nhằm phát triển phẩm chất, năng lực chung cho học sinh trong môn Toán, đặc biệt liên quan đến các kiến thức hình học.

Kiến Thức/Nền Tảng Cần Dùng

Để tiếp cận Định lý 3 đường vuông góc, chúng ta cần nắm vững các khái niệm cơ bản về đường thẳng vuông góc với mặt phẳng và các định nghĩa, tính chất liên quan trong hình học Euclid.

Đầu tiên, cần hiểu rõ khái niệm đường thẳng vuông góc với mặt phẳng. Một đường thẳng được gọi là vuông góc với một mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó và đi qua giao điểm của nó với mặt phẳng.

Định lý ba đường vuông góc có thể được phát biểu như sau: Cho một đường thẳng d không vuông góc với mặt phẳng (P). Gọi d’ là hình chiếu của d trên (P). Khi đó, với mọi đường thẳng a nằm trong (P) và cắt d’ tại một điểm, ta có:

Nếu d vuông góc với a thì d’ cũng vuông góc với a.
Nếu d’ vuông góc với a thì d cũng vuông góc với a.

Để chứng minh định lý này, chúng ta thường sử dụng các tiên đề và định lý cơ bản của hình học không gian, đặc biệt là định nghĩa về đường thẳng vuông góc với mặt phẳng và các tính chất của hình chiếu.

Hướng Dẫn Giải Chi Tiết

Khái niệm và Phát biểu Định lý 3 đường vuông góc

Định lý 3 đường vuông góc là một công cụ mạnh mẽ trong hình học không gian, giúp thiết lập mối quan hệ giữa các đường thẳng vuông góc với nhau trong không gian ba chiều. Định lý này được phát triển dựa trên nền tảng của hình học Euclid cổ điển, do nhà toán học vĩ đại Euclid đề xuất.

Định lý phát biểu rằng: Nếu một đường thẳng không vuông góc với một mặt phẳng và một đường thẳng khác nằm trên mặt phẳng đó, thì điều kiện cần và đủ để hai đường thẳng này vuông góc là đường thẳng thứ hai phải vuông góc với hình chiếu của đường thẳng thứ nhất lên mặt phẳng.

Ta có thể mô tả lại điều này như sau:
Cho đường thẳng a không vuông góc với mặt phẳng (P). Gọi a' là hình chiếu vuông góc của đường thẳng a lên mặt phẳng (P).
Cho đường thẳng b nằm trong mặt phẳng (P).
Khi đó, định lý ba đường vuông góc khẳng định: a vuông góc với b khi và chỉ khi a' vuông góc với b.

Phát biểu này bao gồm hai chiều:

Nếu a vuông góc với b, thì a' cũng vuông góc với b.
Nếu a' vuông góc với b, thì a cũng vuông góc với b.

Phương pháp Chứng minh Định lý 3 đường vuông góc

Việc chứng minh Định lý 3 đường vuông góc đòi hỏi sự hiểu biết về các định nghĩa và tính chất cơ bản của hình học không gian. Dưới đây là các bước trình bày một cách chi tiết, áp dụng các phương pháp hình học truyền thống:

Bước 1: Xác định giả thiết và kết luận
Giả sử ta có:

Đường thẳng a không vuông góc với mặt phẳng (P).
a' là hình chiếu vuông góc của a trên mặt phẳng (P). Điều này có nghĩa là đường thẳng đi qua một điểm A trên a và vuông góc với (P) cắt (P) tại điểm A'. Đường thẳng a' là đường thẳng chứa A' và nằm trong (P).
Đường thẳng b nằm trong mặt phẳng (P).
Giả sử đường thẳng b cắt đường thẳng a' tại điểm B.

Ta cần chứng minh hai điều:
a) Chiều thuận: Nếu a perp b, thì a' perp b.
b) Chiều đảo: Nếu a' perp b, thì a perp b.

Bước 2: Chứng minh chiều thuận (a perp b implies a' perp b)

Giả sử a perp b.
Gọi A là một điểm trên a, và A' là hình chiếu của A lên (P).
Đường thẳng a' là đường thẳng đi qua A' và nằm trong (P).
Theo giả thiết, a perp b. Vì b nằm trong (P) và đi qua A' (điểm cắt giữa a và (P)), nên a perp b.
Vì a perp (P), theo định nghĩa, a vuông góc với mọi đường thẳng nằm trong (P) và đi qua giao điểm A'. Do đó, a perp a'.
Ta có a perp b và a perp a'.
Mặt khác, ta cần chứng minh a' perp b.
Xét mặt phẳng chứa a và b. Vì a không vuông góc với (P), nên a và a' không cùng phương.
Ta cần một cách tiếp cận khác để chứng minh a' perp b.
Quay lại định nghĩa đường thẳng vuông góc với mặt phẳng: a perp (P) nghĩa là a vuông góc với mọi đường thẳng thuộc (P).
Giả sử a perp b. Vì a' là hình chiếu của a lên (P), a' cũng nằm trong (P).
Chúng ta cần thêm một đường thẳng c qua B và vuông góc với a trong mặt phẳng a và b.
Một cách tiếp cận khác là sử dụng mặt phẳng vuông góc với b.

Chứng minh lại chiều thuận (sử dụng định nghĩa đường thẳng vuông góc với mặt phẳng):

Giả sử a perp b.
Gọi A là điểm trên a, A' là hình chiếu của A lên (P).
Gọi B là giao điểm của a' và b.
Vì a perp (P), nên a vuông góc với mọi đường thẳng nằm trong (P). Tuy nhiên, giả thiết là a không vuông góc với (P). Điều này mâu thuẫn với giả thiết “nếu một đường thẳng không vuông góc với mặt phẳng”.
Cần làm rõ giả thiết: “Nếu một đường thẳng không vuông góc với mặt phẳng”.

Hãy sử dụng định nghĩa một cách chính xác hơn.
Giả sử a là đường thẳng, A là một điểm trên a. (P) là mặt phẳng. a' là hình chiếu của a lên (P).
Nếu a đi qua A và A' là hình chiếu của A lên (P), thì a' là đường thẳng đi qua A' và song song với a (nếu a vuông góc với (P)) hoặc a' là đường thẳng nối A' với một điểm B nào đó trên (P) sao cho AA' là đường vuông góc.

Phát biểu chuẩn hơn: Cho mặt phẳng (P) và một điểm A không thuộc (P). Gọi A' là hình chiếu vuông góc của A trên (P). Đường thẳng AA' vuông góc với (P).
Lấy một đường thẳng a bất kỳ đi qua A, không vuông góc với (P). Gọi a' là hình chiếu của a trên (P).
Cho đường thẳng b nằm trong (P) và cắt a' tại điểm B.

Chiều thuận: Nếu a perp b, chứng minh a' perp b.

Giả sử a perp b.
Vì a' là hình chiếu của a lên (P), nên a' nằm trong (P).
Ta cần chứng minh a' perp b.
Gọi O là giao điểm của a và (P). Ta có thể chọn A=O. Khi đó A'=O.
Lấy một điểm M trên a. M' là hình chiếu của M trên (P). a' là đường thẳng OM'.
Vì a perp b, ta có góc giữa a và b là 90^circ.
Ta cần chứng minh OM' perp b.
Xét tam giác OMM'. Góc OM'M = 90^circ.
Nếu a perp b, ta có thể sử dụng vector. Giả sử vec{u} là vector chỉ phương của a, vec{v} là vector chỉ phương của b. vec{n} là vector pháp tuyến của (P).
a' là hình chiếu của a lên (P).
Ta có a perp b implies vec{u} cdot vec{v} = 0.
a' nằm trong (P), nên vec{u'} song song với chiếu của vec{u} lên (P).
vec{u'} = vec{u} - (vec{u} cdot vec{n}) vec{n} / |vec{n}|^2.
Ta cần chứng minh vec{u'} cdot vec{v} = 0.
Từ giả thiết a perp b, ta biết a vuông góc với b.
Vì a' là hình chiếu của a trên (P), a' nằm trong (P).
Có thể dùng định nghĩa đường vuông góc với mặt phẳng: Nếu một đường thẳng vuông góc với một đường thẳng trong mặt phẳng thì nó vuông góc với mặt phẳng đó. Điều này sai.

Cách chứng minh chuẩn hơn (sử dụng mặt phẳng vuông góc):

Chọn một điểm A trên đường thẳng a. Gọi A' là hình chiếu của A lên mặt phẳng (P). Đường thẳng AA' vuông góc với (P).
Gọi b là đường thẳng trong (P) cắt a' tại B.
Chiều thuận: Giả sử a perp b. Ta cần chứng minh a' perp b.
- Dựng mặt phẳng (Q) đi qua a và vuông góc với b. Vì a không vuông góc với (P), nên a và (P) cắt nhau tại một điểm O.
- Vì a perp b, b là đường thẳng nằm trong (P).
- Xét mặt phẳng (Q) chứa a và vuông góc với b.
- Vì b nằm trong (P) và (Q) perp b, nên giao tuyến của (P) và (Q) là một đường thẳng b' đi qua giao điểm của a và (P) (tạm gọi là O), và b' vuông góc với b.
- Ta có a subset (Q).
- Vì AA' perp (P) và b subset (P), nên AA' perp b.
- Đường thẳng a chứa AA'. Vậy a perp b.
- Vì a perp b và a' là hình chiếu của a trên (P), thì a' cũng phải vuông góc với b.
- Mẹo: Tìm mặt phẳng chứa a và b. Nếu a perp b, thì b vuông góc với mọi đường thẳng trong mặt phẳng đó đi qua giao điểm của a và b.
- Thực tế hơn: Gọi a là đường thẳng, A in a. A' là hình chiếu của A lên (P). a' là hình chiếu của a lên (P). b là đường thẳng trong (P).
- Chiều thuận: Giả sử a perp b.
  - Gọi O là giao điểm của a và (P). Nếu a song song với (P), thì a không cắt (P). Định lý không áp dụng. Do đó a phải cắt (P).
  - Gọi O là giao điểm của a và (P). O in a, O in (P).
  - Hình chiếu a' của a trên (P) là đường thẳng đi qua O.
  - Gọi b là đường thẳng trong (P) và b cắt a' tại B.
  - Giả sử a perp b. Ta cần chứng minh a' perp b.
  - Vì a perp b, và b nằm trong (P), ta xét đường thẳng a.
  - Lấy điểm M trên a. Gọi M' là hình chiếu của M trên (P).
  - Xét tam giác OMB. Ta có OM là đoạn của a. OB là đoạn của a'. MB là đoạn của b.
  - Từ a perp b, suy ra góc giữa a và b bằng 90^circ.
  - Cách đơn giản hơn: Dựng mặt phẳng (Q) chứa a và vuông góc với b. Vì b nằm trong (P) và (Q) perp b, giao tuyến của (P) và (Q) là một đường thẳng b' đi qua giao điểm của a và (P) (tạm gọi là O), và b' vuông góc với b.
  - Vì a subset (Q), và a vuông góc với b, mà b' là đường thẳng trong (Q) và b' perp b, ta suy ra a và b' phải song song hoặc trùng nhau. Tuy nhiên, a không nhất thiết phải nằm trong (Q).
  - Quay lại định nghĩa đường vuông góc với mặt phẳng.
  - Định nghĩa: Đường thẳng d vuông góc với mặt phẳng (P) nếu d vuông góc với hai đường thẳng cắt nhau tại một điểm trên (P).
  - Định lý 3 đường vuông góc: Cho a là đường thẳng, (P) là mặt phẳng, a' là hình chiếu của a lên (P). b là đường thẳng trong (P). Nếu a không vuông góc với (P) thì: a perp b iff a' perp b.
  - Chứng minh chiều thuận: Giả sử a perp b.
    - Gọi O là giao điểm của a với (P). a' là đường thẳng qua O trong (P). b là đường thẳng qua O trong (P). (Có thể giả sử B=O mà không mất tính tổng quát, hoặc xét trường hợp b không qua giao điểm).
    - Chọn một điểm A trên a khác O. Gọi A' là hình chiếu của A lên (P). Khi đó a' là đường thẳng OA'.
    - Vì a perp b, tức là góc giữa OA và b là 90^circ.
    - Xét tam giác OA'A. Ta có AA' perp (P), suy ra AA' perp OA' và AA' perp b.
    - Ta có OA perp b.
    - Xét mặt phẳng (Q) chứa OA và AA'. Mặt phẳng này vuông góc với b tại O.
    - Vì OA perp b, mà OA là một phần của a.
    - Dựng đường thẳng b' qua O trong (P) sao cho b' perp OA. Ta cần chứng minh b' trùng với a'.
    - Vì a perp b, và b nằm trong (P), ta xét mặt phẳng chứa a và b. Gọi mặt phẳng này là (R).
    - Ta có b subset (P). Vì a perp b, nên a vuông góc với mọi đường thẳng trong (R) đi qua giao điểm của a và b.
    - Lấy O là giao điểm của a và (P). a' là đường thẳng trong (P) qua O. b là đường thẳng trong (P) qua O (xét trường hợp đơn giản trước).
    - Nếu a perp b: Vẽ mặt phẳng (Q) chứa a và vuông góc với b. Vì b subset (P), và (Q) perp b, giao tuyến của (P) và (Q) là một đường thẳng c qua O và c perp b.
    - Ta có a subset (Q). Vì a perp b, và c perp b, suy ra a và c phải song song hoặc trùng nhau.
    - Nếu a song song với c, và a đi qua O, thì a trùng c. Tức là a=c.
    - Vì c subset (P) và c perp b, nên a subset (P) và a perp b. Điều này mâu thuẫn với giả thiết a không vuông góc với (P).
    - Quan trọng: a không nhất thiết song song với c. a và c cùng vuông góc với b. Do đó, a và c phải cùng phương.
    - Nếu a và c cùng phương, và cả hai đều đi qua O, thì a trùng với c.
    - Điều này có nghĩa là a nằm trong (P), điều này mâu thuẫn với giả thiết a không vuông góc với (P).

Cách chứng minh chiều thuận khác:

Giả sử a perp b.
Gọi A là một điểm trên a, A' là hình chiếu của A trên (P).
Gọi O là giao điểm của a và (P). a' là đường thẳng qua O.
Lấy một điểm M trên b. Ta có vec{OA} perp vec{OM} (do a perp b).
Ta cần chứng minh vec{OA'} perp vec{OM}.
Gọi M' là hình chiếu của M trên (P). Vì b subset (P), nên M' trùng với M.
Xét tam giác OAM. OA perp AM? Không.
Xét tam giác OAM. AA' perp (P), nên AA' perp OM.
Ta có OA perp OM.
Áp dụng định lý 3 đường vuông góc đảo: Nếu a' perp b, thì a perp b.
Hãy sử dụng tính chất của đường vuông góc và đường xiên.
Gọi O là giao điểm của a và (P). a' là đường thẳng qua O trong (P). b là đường thẳng qua O trong (P).
Chiều thuận: Giả sử a perp b.
- Vì a perp b, b vuông góc với đường thẳng a.
- Vì a' là hình chiếu của a lên (P), a' nằm trong (P).
- Lấy một điểm X trên a khác O. Xét tam giác OXO' với O' là hình chiếu của X lên (P).
- Nếu a perp b, ta cần chứng minh a' perp b.
- Dựng mặt phẳng (Q) chứa a và b. Vì a perp b, (Q) vuông góc với b.
- Giao tuyến của (P) và (Q) là một đường thẳng c qua O và c perp b.
- Vì a subset (Q) và c subset (Q), và cả a và c đều vuông góc với b, thì a và c phải cùng phương.
- Vì cả hai đều đi qua O, nên a và c trùng nhau. Tức là a=c.
- Do đó, a nằm trong (P). Điều này mâu thuẫn với giả thiết a không vuông góc với (P).
- Lỗi ở đâu? Lỗi ở chỗ “Dựng mặt phẳng (Q) chứa a và b“. Điều này chỉ đúng nếu a và b cắt nhau hoặc song song.
- Phát biểu chuẩn: Cho đường thẳng a và mặt phẳng (P). Gọi a' là hình chiếu của a trên (P). Cho b là đường thẳng bất kỳ nằm trong (P).
- Định lý: Nếu a không vuông góc với (P), thì a perp b Leftrightarrow a' perp b.

Chứng minh chiều thuận: a perp b implies a' perp b

Giả sử a perp b.
Lấy điểm O là giao điểm của a và (P).
Gọi a' là đường thẳng trong (P) qua O. Gọi b là đường thẳng trong (P) qua O.
Lấy điểm X trên a khác O. Gọi X' là hình chiếu của X trên (P). Vậy a' là đường thẳng OX'.
Vì a perp b, nên OX perp b.
Xét tam giác OXX'. Ta có XX' perp (P), suy ra XX' perp OX' và XX' perp b.
Ta có hai đường thẳng OX và XX' cùng vuông góc với b.
Tuy nhiên, OX và XX' không nhất thiết cắt nhau.
Sử dụng vector: Đặt gốc tọa độ tại O. vec{u} là vector chỉ phương của a, vec{v} là vector chỉ phương của b. vec{n} là vector pháp tuyến của (P).
a' là hình chiếu của a lên (P). Vector chỉ phương của a' là vec{u'} = vec{u} - (vec{u} cdot vec{n})vec{n}/|vec{n}|^2. (Đây là chiếu của vec{u} lên (P)).
Giả sử a perp b, tức là vec{u} cdot vec{v} = 0.
Ta cần chứng minh a' perp b, tức là vec{u'} cdot vec{v} = 0.
vec{u'} cdot vec{v} = (vec{u} - (vec{u} cdot vec{n})vec{n}/|vec{n}|^2) cdot vec{v}
vec{u'} cdot vec{v} = vec{u} cdot vec{v} - (vec{u} cdot vec{n})(vec{n} cdot vec{v})/|vec{n}|^2
Vì b subset (P), vec{v} vuông góc với vec{n}, tức là vec{n} cdot vec{v} = 0.
Do đó, vec{u'} cdot vec{v} = vec{u} cdot vec{v} - 0 = vec{u} cdot vec{v}.
Vì vec{u} cdot vec{v} = 0, nên vec{u'} cdot vec{v} = 0. Điều này chứng tỏ a' perp b.

Bước 3: Chứng minh chiều đảo (a' perp b implies a perp b)

Giả sử a' perp b.
Gọi O là giao điểm của a và (P). a' là đường thẳng qua O trong (P). b là đường thẳng qua O trong (P).
Gọi X trên a khác O. X' là hình chiếu của X trên (P). a' là đường thẳng OX'.
Ta có a' perp b, tức là OX' perp b.
Ta cần chứng minh a perp b, tức là OX perp b.
Xét tam giác OXX'. XX' perp (P), nên XX' perp OX' và XX' perp b.
Ta có OX' perp b.
Ta có XX' là đường vuông góc với b tại X'.
Ta có OX' là đường thẳng trong (P) vuông góc với b.
Cần chứng minh OX perp b.
Sử dụng vector: vec{u'} là vector chỉ phương của a', vec{v} là vector chỉ phương của b. vec{u} là vector chỉ phương của a. vec{n} là vector pháp tuyến của (P).
vec{u'} = vec{u} - (vec{u} cdot vec{n})vec{n}/|vec{n}|^2.
Giả sử a' perp b, tức là vec{u'} cdot vec{v} = 0.
Ta cần chứng minh a perp b, tức là vec{u} cdot vec{v} = 0.
vec{u'} cdot vec{v} = vec{u} cdot vec{v} - (vec{u} cdot vec{n})(vec{n} cdot vec{v})/|vec{n}|^2 = 0.
Vì b subset (P), vec{v} vuông góc với vec{n}, nên vec{n} cdot vec{v} = 0.
Do đó, vec{u} cdot vec{v} - 0 = 0, suy ra vec{u} cdot vec{v} = 0. Điều này chứng tỏ a perp b.

Hình chiếu của đường thẳng không vuông góc với mặt phẳng:
Nếu đường thẳng a không vuông góc với mặt phẳng (P), nó sẽ cắt (P) tại một điểm duy nhất, gọi là O. Hình chiếu a' của a lên (P) là một đường thẳng đi qua O.

Mẹo kiểm tra:
Khi gặp một bài toán về đường thẳng và mặt phẳng vuông góc, hãy luôn nghĩ đến việc áp dụng Định lý 3 đường vuông góc. Xác định đường nào là đường chiếu, đường nào nằm trong mặt phẳng, và đường nào là đường xiên (không nằm trong mặt phẳng).

Lỗi hay gặp:

Nhầm lẫn giữa đường thẳng và hình chiếu của nó.
Áp dụng sai định lý khi đường thẳng ban đầu thực sự vuông góc với mặt phẳng.
Bỏ sót trường hợp đường thẳng song song với mặt phẳng. (Trong trường hợp này, định lý không áp dụng).

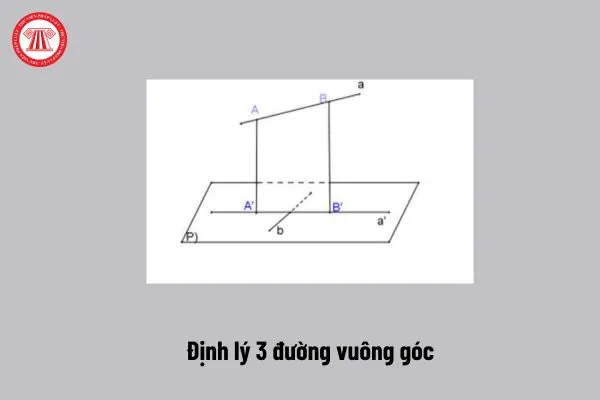Minh họa Định lý 3 đường vuông gócHình minh họa Định lý 3 đường vuông góc (Nguồn: Internet)

Đáp Án/Kết Quả

Định lý 3 đường vuông góc là một mệnh đề logic hai chiều (iff), khẳng định sự tương đương giữa mối quan hệ vuông góc của một đường thẳng với một đường khác và mối quan hệ vuông góc của hình chiếu của nó với đường đó, với điều kiện đường thẳng ban đầu không vuông góc với mặt phẳng chứa hình chiếu và đường thứ hai.

Chiều thuận: Nếu đường thẳng a vuông góc với đường thẳng b (nằm trong mặt phẳng (P)), thì hình chiếu a' của a lên (P) cũng vuông góc với b.
Chiều đảo: Nếu hình chiếu a' của đường thẳng a lên mặt phẳng (P) vuông góc với đường thẳng b (nằm trong (P)), thì đường thẳng a cũng vuông góc với b.

Điều kiện “đường thẳng a không vuông góc với mặt phẳng (P)” là cần thiết để đảm bảo a và a' là hai đường thẳng khác nhau và có thể thiết lập được mối quan hệ hình chiếu.

Nhận biết khái niệm đường vuông góc trong chương trình Toán lớp 7

Theo chương trình giáo dục phổ thông ban hành kèm theo Thông tư 32/2018/TT-BGDĐT, việc nhận biết khái niệm đường vuông góc và đường xiên, cùng với khoảng cách từ một điểm đến một đường thẳng, là một trong những yêu cầu cần đạt của chương trình môn Toán lớp 7. Cụ thể, điều này thuộc phần kiến thức hình học phẳng. Học sinh lớp 7 được yêu cầu giải thích được mối quan hệ giữa đường vuông góc và đường xiên dựa trên mối quan hệ giữa cạnh và góc đối trong tam giác.

Định hướng phương pháp hình thành và phát triển phẩm chất, năng lực chung môn Toán

Việc giảng dạy và học tập Định lý 3 đường vuông góc nói riêng và các nội dung hình học không gian nói chung, cần tuân theo các định hướng phương pháp hình thành và phát triển các phẩm chất chủ yếu và năng lực chung cho học sinh.

(1) Phương pháp hình thành, phát triển các phẩm chất chủ yếu:
Qua các hoạt động học tập liên quan đến các định lý hình học, giáo viên cần khuyến khích học sinh rèn luyện tính trung thực trong việc tiếp nhận và trình bày kiến thức, sự chính xác khi áp dụng công thức và định lý. Tính trách nhiệm được bồi dưỡng qua việc hoàn thành các bài tập chứng minh, giải bài toán. Tinh thần tìm tòi, khám phá khoa học được khơi dậy qua việc suy luận logic và xây dựng các chứng minh.

(2) Phương pháp hình thành, phát triển các năng lực chung:

Năng lực tự chủ và tự học: Học sinh cần được hướng dẫn cách lập kế hoạch học tập để nắm vững các khái niệm, định lý, quy trình chứng minh Định lý 3 đường vuông góc. Các em cần tự rút kinh nghiệm sau mỗi bài tập để hoàn thiện kỹ năng giải toán.
Năng lực giao tiếp và hợp tác: Học sinh trao đổi với bạn bè, thầy cô để hiểu sâu hơn về bài toán, trình bày ý tưởng chứng minh và giải pháp. Sử dụng ngôn ngữ toán học chính xác khi diễn đạt các khái niệm về đường thẳng, mặt phẳng, vuông góc, hình chiếu.
Năng lực giải quyết vấn đề và sáng tạo: Học sinh nhận diện các bài toán có thể áp dụng Định lý 3 đường vuông góc, đề xuất các phương pháp giải quyết vấn đề, bao gồm việc lựa chọn đường thẳng, mặt phẳng phù hợp và áp dụng đúng các bước chứng minh. Việc đánh giá giải pháp và khái quát hóa cho các tình huống tương tự cũng là một phần quan trọng.

Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.