Định Lý Cosin: Công Thức, Ứng Dụng Và Bài Tập Minh Họa Chi Tiết

by Thầy Đông · January 7, 2026

Rate this post

Định lý cosin là một công cụ toán học nền tảng trong hình học phẳng, không chỉ giúp chúng ta giải quyết các bài toán phức tạp về tam giác mà còn mở ra cánh cửa hiểu biết về nhiều hiện tượng trong thế giới thực. Bài viết này sẽ đi sâu vào khám phá công thức cosin, cách áp dụng và những ứng dụng đa dạng của nó trong nhiều lĩnh vực.

Đề Bài

Trong chương trình toán phổ thông, có những công thức không chỉ giúp giải bài tập trên lớp mà còn trở thành “chìa khóa” để lý giải nhiều hiện tượng trong thực tế. Một trong số đó là định lý cosin – công cụ quan trọng để tính toán trong các tam giác bất kỳ. Bài viết này sẽ cùng bạn tìm hiểu chi tiết hơn về định lý cosin.

định lý cosin 1.jpg

Phân Tích Yêu Cầu

Bài viết gốc cung cấp một cái nhìn tổng quan về định lý cosin, bao gồm định nghĩa, cách chứng minh cơ bản, các trường hợp áp dụng điển hình (tính cạnh, tính góc, giải tam giác tổng quát), một ví dụ bài tập thực tế và các ứng dụng trong đời sống, giáo dục, kỹ thuật, hàng hải, hàng không và công nghệ. Yêu cầu của bài viết mới là tái cấu trúc và mở rộng nội dung này theo cấu trúc chuẩn SEO và chuẩn học thuật, tập trung vào việc làm rõ công thức, quy trình áp dụng và cung cấp thêm các ví dụ minh họa chi tiết, các mẹo kiểm tra và lỗi thường gặp, đồng thời tuân thủ chặt chẽ quy tắc hiển thị công thức KaTeX.

Kiến Thức/Nền Tảng Cần Dùng

Để hiểu và áp dụng định lý cosin, chúng ta cần nắm vững các kiến thức sau:

1. Tam Giác Bất Kỳ

Một tam giác bất kỳ là một hình đa giác có ba cạnh và ba góc. Các yếu tố cơ bản của tam giác bao gồm ba cạnh (thường ký hiệu là $a, b, c$) và ba góc đối diện với các cạnh đó (ký hiệu lần lượt là $A, B, C$). Tổng ba góc trong một tam giác luôn bằng 180 độ ( $A + B + C = 180^\circ$ ).

2. Các Hàm Lượng Giác Cơ Bản

Định lý cosin liên quan trực tiếp đến hàm cosin của một góc. Chúng ta cần nhớ giá trị cơ bản của hàm cosin cho các góc đặc biệt:

$\cos 0^\circ = 1$
$\cos 30^\circ = \dfrac{\sqrt{3}}{2}$
$\cos 45^\circ = \dfrac{\sqrt{2}}{2}$
$\cos 60^\circ = \dfrac{1}{2}$
$\cos 90^\circ = 0$
$\cos 120^\circ = -\dfrac{1}{2}$
$\cos 180^\circ = -1$

Cũng cần hiểu mối quan hệ giữa các góc trong tam giác và giá trị của hàm cosin. Ví dụ, nếu một góc lớn hơn $90^\circ$ (góc tù), thì giá trị cosin của nó sẽ âm.

3. Định Lý Pytago

Định lý Pytago là trường hợp đặc biệt của định lý cosin khi tam giác là tam giác vuông. Phát biểu của định lý Pytago là: “Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông”. Công thức: $c^2 = a^2 + b^2$ , với $c$ là cạnh huyền và $a, b$ là hai cạnh góc vuông. Việc hiểu định lý Pytago giúp nhận ra định lý cosin là một mở rộng tổng quát hơn.

4. Nguyên Tắc Biến Đổi Đại Số

Các phép biến đổi đại số cơ bản như cộng, trừ, nhân, chia, bình phương, khai căn, đưa thừa số ra ngoài dấu căn sẽ được sử dụng thường xuyên khi áp dụng định lý cosin để tính toán.

Hướng Dẫn Giải Chi Tiết

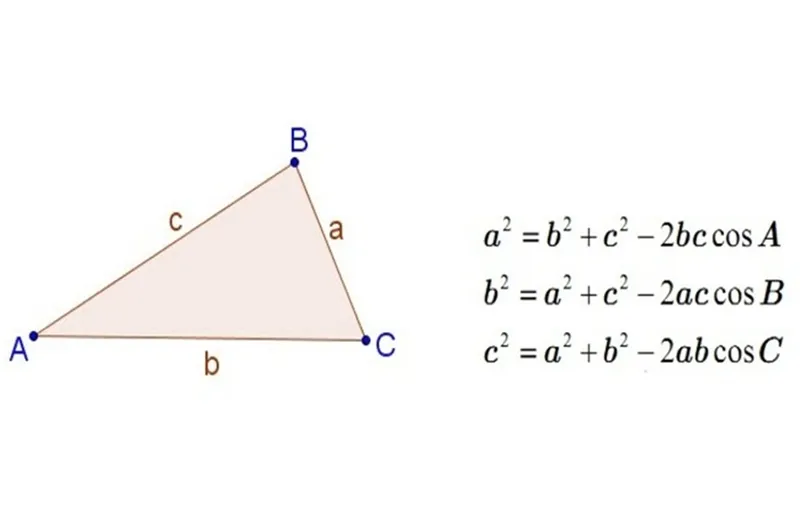
Định lý cosin phát biểu rằng: “Bình phương độ dài một cạnh của tam giác bằng tổng bình phương độ dài hai cạnh còn lại trừ đi hai lần tích của độ dài hai cạnh đó với cosin của góc xen giữa chúng.”

Cho tam giác $ABC$ với độ dài ba cạnh lần lượt là $a, b, c$ và các góc đối diện tương ứng là $A, B, C$. Ta có các công thức sau:

Tính cạnh $c$ khi biết $a, b$ và góc $C$:
$c^2 = a^2 + b^2 - 2ab \cos C$
Tính cạnh $a$ khi biết $b, c$ và góc $A$:
$a^2 = b^2 + c^2 - 2bc \cos A$
Tính cạnh $b$ khi biết $a, c$ và góc $B$:
$b^2 = a^2 + c^2 - 2ac \cos B$

Từ các công thức trên, chúng ta có thể suy ra công thức để tính góc khi biết độ dài ba cạnh:

Tính góc $C$ khi biết $a, b, c$:
$\cos C = \dfrac{a^2 + b^2 - c^2}{2ab}$
Tính góc $A$ khi biết $a, b, c$:
$\cos A = \dfrac{b^2 + c^2 - a^2}{2bc}$
Tính góc $B$ khi biết $a, b, c$:
$\cos B = \dfrac{a^2 + c^2 - b^2}{2ac}$

Trường Hợp Đặc Biệt: Quan Hệ với Định Lý Pytago

Khi một trong các góc của tam giác là $90^\circ$ , ví dụ góc $C = 90^\circ$ . Ta biết $\cos 90^\circ = 0$ .
Thay vào công thức:
$c^2 = a^2 + b^2 - 2ab \cos 90^\circ$
$c^2 = a^2 + b^2 - 2ab \times 0$
$c^2 = a^2 + b^2$
Đây chính là định lý Pytago. Điều này khẳng định định lý cosin là một sự tổng quát hóa của định lý Pytago cho mọi tam giác, không chỉ tam giác vuông.

Ví Dụ 1: Tính Cạnh Khi Biết Hai Cạnh và Góc Xen Giữa

Đề bài: Cho tam giác $ABC$ có độ dài cạnh $a = 5text{ cm}$ , cạnh $b = 7text{ cm}$ và góc $C = 60^\circ$ . Tính độ dài cạnh $c$.

Phân tích: Chúng ta biết hai cạnh và góc xen giữa, do đó có thể áp dụng trực tiếp công thức của định lý cosin để tìm cạnh còn lại.

Các bước giải:

Xác định các giá trị đã cho: $a = 5$ , $b = 7$ , $C = 60^\circ$ .
Áp dụng công thức: $c^2 = a^2 + b^2 - 2ab \cos C$ .
Thay số vào công thức:
$c^2 = 5^2 + 7^2 - 2 \times 5 \times 7 \times \cos 60^\circ$
$c^2 = 25 + 49 - 2 \times 35 \times \dfrac{1}{2}$
$c^2 = 74 - 35$
$c^2 = 39$
Tìm $c$:
$c = \sqrt{39}$
$c \approx 6.245 \text{ cm}$

Đáp án: Độ dài cạnh $c$ xấp xỉ $6.245 \text{ cm}$ .

Mẹo kiểm tra:

Nếu góc $C$ nhỏ hơn $90^\circ$ (nhọn), thì $c^2$ sẽ nhỏ hơn $a^2 + b^2$ . Trong ví dụ này, $39 < 25 + 49 = 74[/katex], là hợp lý.</li> <li>Nếu góc $C$ bằng [katex]90^\circ$ , $c^2$ sẽ bằng $a^2 + b^2$ .
Nếu góc $C$ lớn hơn $90^\circ$ (tù), thì $c^2$ sẽ lớn hơn $a^2 + b^2$ .

Lỗi hay gặp:

Nhầm lẫn giữa các cạnh và góc đối diện.
Quên dấu trừ trong công thức.
Sử dụng sai giá trị cosin của góc (ví dụ: $\cos 60^\circ = \sqrt{3}/2$ thay vì $1/2$ ).
Tính toán sai bình phương hoặc căn bậc hai.

Ví Dụ 2: Tính Góc Khi Biết Ba Cạnh

Đề bài: Cho tam giác $ABC$ có độ dài ba cạnh lần lượt là $a = 6text{ cm}$ , $b = 8text{ cm}$ và $c = 10text{ cm}$ . Tính độ lớn các góc $A, B, C$.

Phân tích: Chúng ta có độ dài cả ba cạnh, do đó có thể sử dụng các công thức suy ra từ định lý cosin để tìm từng góc.

Các bước giải:

Tính góc $C$:
Ta dùng công thức: $\cos C = \dfrac{a^2 + b^2 - c^2}{2ab}$
Thay số:
$\cos C = \dfrac{6^2 + 8^2 - 10^2}{2 \times 6 \times 8}$
$\cos C = \dfrac{36 + 64 - 100}{96}$
$\cos C = \dfrac{100 - 100}{96}$
$\cos C = \dfrac{0}{96} = 0$
Vì $\cos C = 0$ , suy ra $C = 90^\circ$ .
Kiểm tra: Nhận thấy $a^2 + b^2 = 6^2 + 8^2 = 36 + 64 = 100$ , và $c^2 = 10^2 = 100$ . Vì $a^2 + b^2 = c^2$ , tam giác này là tam giác vuông tại $C$ theo định lý Pytago đảo. Kết quả $C = 90^\circ$ là chính xác.
Tính góc $A$:
Ta dùng công thức: $\cos A = \dfrac{b^2 + c^2 - a^2}{2bc}$
Thay số:
$\cos A = \dfrac{8^2 + 10^2 - 6^2}{2 \times 8 \times 10}$
$\cos A = \dfrac{64 + 100 - 36}{160}$
$\cos A = \dfrac{128}{160}$
$\cos A = \dfrac{4}{5} = 0.8$
Sử dụng máy tính bỏ túi, ta tìm được $A = arccos(0.8) \approx 36.87^\circ$ .
Tính góc $B$:
Ta có thể dùng công thức tương tự hoặc tận dụng tổng ba góc của tam giác: $A + B + C = 180^\circ$ .
$B = 180^\circ - A - C$
$B \approx 180^\circ - 36.87^\circ - 90^\circ$
$B \approx 53.13^\circ$ .

Đáp án: Các góc của tam giác là $A \approx 36.87^\circ$ , $B \approx 53.13^\circ$ , $C = 90^\circ$ .

Mẹo kiểm tra:

Tổng ba góc phải bằng $180^\circ$ : $36.87^\circ + 53.13^\circ + 90^\circ = 180^\circ$ .
Góc đối diện với cạnh lớn nhất là góc lớn nhất, và ngược lại. Cạnh $c=10$ là lớn nhất, góc $C=90^\circ$ là lớn nhất. Cạnh $a=6$ là nhỏ nhất, góc $A \approx 36.87^\circ$ là nhỏ nhất.

Lỗi hay gặp:

Nhầm lẫn công thức tính cosin của các góc khác nhau.
Sai sót trong phép tính bình phương, cộng trừ, nhân chia.
Sử dụng máy tính không đúng chế độ (độ hay radian) khi tính $arccos$.
Không kiểm tra lại kết quả bằng định lý Pytago hoặc tổng ba góc.

Ví Dụ 3: Giải Tam Giác Tổng Quát

"Giải tam giác" có nghĩa là tìm độ dài ba cạnh và số đo ba góc của tam giác đó. Định lý cosin thường được sử dụng kết hợp với định lý sin để giải quyết trường hợp này.

Các trường hợp cần giải tam giác:

Cạnh - Góc - Cạnh (CGC): Biết hai cạnh và góc xen giữa (ví dụ: biết $a, b, C$).
- Bước 1: Sử dụng định lý cosin để tìm cạnh còn lại (ví dụ: $c^2 = a^2 + b^2 - 2ab \cos C$ ).
- Bước 2: Sử dụng định lý sin để tìm một trong hai góc còn lại (ví dụ: $\dfrac{a}{\sin A} = \dfrac{c}{\sin C}$ ). Từ đó, ta có $\sin A = \dfrac{a \sin C}{c}$ .
- Bước 3: Tính góc còn lại bằng tổng ba góc: $B = 180^\circ - A - C$ .
Cạnh - Cạnh - Cạnh (CCC): Biết độ dài ba cạnh (ví dụ: biết $a, b, c$).
- Bước 1: Sử dụng định lý cosin để tìm một góc (ví dụ: $\cos A = \dfrac{b^2 + c^2 - a^2}{2bc}$ ).
- Bước 2: Sử dụng định lý sin để tìm một góc khác (ví dụ: $\sin B = \dfrac{b \sin A}{a}$ ).
- Bước 3: Tính góc còn lại bằng tổng ba góc: $C = 180^\circ - A - B$ .

Lưu ý quan trọng khi sử dụng định lý sin: Định lý sin cho ta giá trị $\sin$ , nhưng một giá trị sin có thể tương ứng với hai góc trong khoảng từ $0^\circ$ đến $180^\circ$ (ví dụ: $\sin 30^\circ = \sin 150^\circ = 1/2$ ). Tuy nhiên, trong một tam giác, chỉ có thể có tối đa một góc tù. Khi sử dụng định lý sin để tìm góc thứ hai, nếu góc đó là góc tù, nó sẽ đối diện với cạnh lớn hơn. Cách an toàn là ưu tiên tính các góc nhọn trước hoặc sử dụng định lý cosin để tìm góc còn lại nếu có thể.

Ví dụ áp dụng cho trường hợp CGC:
Cho tam giác $ABC$ với $a = 7$ , $c = 5$ , và $B = 120^\circ$ .

Tìm cạnh $b$:
$b^2 = a^2 + c^2 - 2ac \cos B$
$b^2 = 7^2 + 5^2 - 2 \times 7 \times 5 \times \cos 120^\circ$
$b^2 = 49 + 25 - 70 \times (-\dfrac{1}{2})$
$b^2 = 74 + 35 = 109$
$b = \sqrt{109} \approx 10.44$
Tìm góc $A$:
Sử dụng định lý sin: $\dfrac{a}{\sin A} = \dfrac{b}{\sin B}$
$\sin A = \dfrac{a \sin B}{b} = \dfrac{7 \times \sin 120^\circ}{\sqrt{109}} = \dfrac{7 \times \dfrac{\sqrt{3}}{2}}{\sqrt{109}} \approx \dfrac{7 \times 0.866}{10.44} \approx 0.58$
$A = arcsin(0.58) \approx 35.46^\circ$ .
Tìm góc $C$:
$C = 180^\circ - B - A \approx 180^\circ - 120^\circ - 35.46^\circ \approx 24.54^\circ$ .

Vậy, tam giác có các cạnh $a=7, b=\sqrt{109}, c=5$ và các góc $A \approx 35.46^\circ, B=120^\circ, C \approx 24.54^\circ$ .

Ứng Dụng Định Lý Cosin Trong Đời Sống và Khoa Học

Định lý cosin không chỉ là một công cụ lý thuyết khô khan trong sách giáo khoa mà còn là nền tảng cho nhiều ứng dụng thực tế quan trọng.

1. Trong Giáo Dục và Nghiên Cứu Toán Học

Vai trò cốt lõi của định lý cosin là trong chương trình giảng dạy toán học trung học phổ thông và đại học. Nó giúp học sinh:

Nắm vững kiến thức hình học: Hiểu sâu hơn về mối quan hệ giữa các cạnh và góc trong mọi loại tam giác.
Phát triển tư duy logic: Luyện tập kỹ năng phân tích bài toán, biến đổi công thức và suy luận chặt chẽ.
Giải các bài toán phức tạp: Là nền tảng để giải các bài toán hình học không gian, lượng giác, và các chủ đề nâng cao khác.

2. Trong Kỹ Thuật, Xây Dựng và Đo Đạc

Ngành kỹ thuật, xây dựng và đo đạc địa chính là những lĩnh vực mà định lý cosin được ứng dụng thường xuyên:

Thiết kế và thi công: Kỹ sư sử dụng định lý cosin để tính toán khoảng cách, góc nghiêng, chiều cao của các cấu kiện công trình, đảm bảo độ chính xác và an toàn. Ví dụ, khi thiết kế mái nhà, dầm cầu, hoặc các công trình có hình dạng phức tạp.
Đo đạc địa hình: Trong khảo sát địa chất, xây dựng bản đồ, kỹ sư trắc địa thường phải đo đạc khoảng cách giữa các điểm trên mặt đất mà không thể tiếp cận trực tiếp. Họ sẽ đo đạc các khoảng cách có thể tiếp cận được và các góc tạo thành, sau đó dùng định lý cosin để tính toán khoảng cách thực tế giữa các điểm đó.

định lý cosin 3.jpg

3. Trong Hàng Hải và Hàng Không

Ngành hàng hải và hàng không phụ thuộc rất nhiều vào các phép tính toán học chính xác để định vị và dẫn đường:

Hàng hải: Thuyền trưởng và hoa tiêu sử dụng các phiên bản mở rộng của định lý cosin, như định lý cosin trên mặt cầu (spherical law of cosines), để tính toán khoảng cách và góc giữa các vị trí trên bề mặt cong của Trái Đất. Điều này cực kỳ quan trọng cho việc lập hải trình an toàn và hiệu quả.
Hàng không: Phi công sử dụng các nguyên tắc tương tự để tính toán lộ trình bay, góc lái, và ước tính thời gian di chuyển. Các hệ thống dẫn đường trên máy bay tích hợp các thuật toán dựa trên định lý cosin để liên tục cập nhật vị trí và hướng đi.

4. Trong Công Nghệ Định Vị (GPS) và Viễn Thám

Hệ thống Định vị Toàn cầu (GPS) và các công nghệ viễn thám hiện đại là những minh chứng rõ ràng nhất về sức mạnh ứng dụng của các nguyên lý toán học:

GPS: Các thiết bị GPS nhận tín hiệu từ nhiều vệ tinh. Bằng cách đo thời gian tín hiệu di chuyển từ vệ tinh đến thiết bị, hệ thống có thể tính toán khoảng cách giữa thiết bị và mỗi vệ tinh. Các phương pháp tính toán tam giác hóa hoặc đa giác hóa, mà nền tảng là các nguyên lý về khoảng cách và góc (bao gồm cả định lý cosin mở rộng), giúp xác định chính xác vị trí địa lý của người dùng trên Trái Đất.
Viễn thám: Trong phân tích dữ liệu ảnh vệ tinh, các nhà khoa học sử dụng các mô hình toán học phức tạp, trong đó có các phép tính liên quan đến hình học và khoảng cách, để đo đạc và phân tích các đặc điểm trên bề mặt Trái Đất, như diện tích rừng, mực nước biển, hoặc biến đổi khí hậu.

định lý cosin 4.png

5. Trong Đời Sống Hàng Ngày

Ngay cả trong các hoạt động thông thường, định lý cosin vẫn có thể được áp dụng một cách gián tiếp hoặc trực quan:

Thiết kế nội thất: Ước lượng khoảng cách đặt đồ vật, bố trí không gian sao cho hợp lý.
Lắp đặt thiết bị: Tính toán góc đặt camera an ninh, loa, hoặc các thiết bị yêu cầu góc nhìn chính xác.
Đo đạc không gian: Khi cần biết khoảng cách giữa hai điểm không thể tiếp cận trực tiếp trong nhà hoặc vườn.

định lý cosin 5.png

Đáp Án/Kết Quả

Định lý cosin là công thức cơ bản nhưng vô cùng mạnh mẽ trong toán học, cho phép chúng ta tính toán mối quan hệ giữa ba cạnh và ba góc của bất kỳ tam giác nào. Nó có thể được sử dụng để:

Tính độ dài một cạnh khi biết hai cạnh còn lại và góc xen giữa.
Tính độ lớn của một góc khi biết độ dài cả ba cạnh.
Giải tam giác bất kỳ (tìm tất cả các cạnh và góc còn thiếu).

Là sự tổng quát hóa của định lý Pytago, định lý cosin mở rộng khả năng phân tích và giải quyết vấn đề trong hình học phẳng. Các ứng dụng của nó trải dài từ giáo dục, kỹ thuật, xây dựng, đo đạc, cho đến các lĩnh vực công nghệ cao như định vị toàn cầu và dẫn đường hàng không, cho thấy vai trò không thể thiếu của nó trong việc mô tả và hiểu thế giới xung quanh chúng ta.

Tóm lại, định lý cosin không chỉ là một công thức toán học cần ghi nhớ cho kỳ thi, mà còn là một công cụ thực tiễn thiết yếu, giúp chúng ta đo lường, tính toán và giải quyết các vấn đề trong vô số tình huống khác nhau của cuộc sống và khoa học kỹ thuật. Việc nắm vững và vận dụng thành thạo định lý này sẽ mang lại lợi ích to lớn, từ việc học tập hiệu quả đến việc áp dụng sáng tạo vào thực tiễn.

Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.