Định Lý Talet Đảo và Hệ Quả: Khái Niệm, Chứng Minh và Ứng Dụng

by Thầy Đông · January 7, 2026

Rate this post

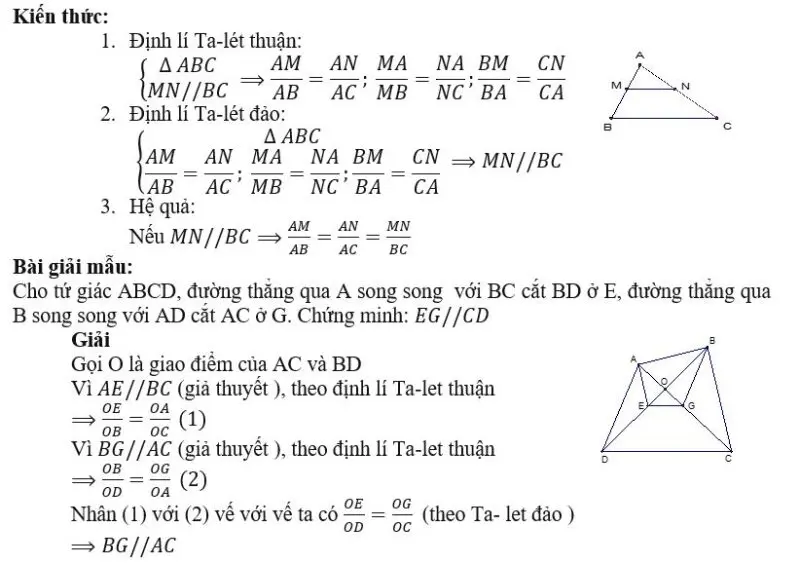
Trong hình học, định lý Talet đảo và hệ quả đóng vai trò quan trọng trong việc chứng minh sự song song của các đường thẳng dựa trên tỉ lệ của các đoạn thẳng. Hiểu rõ định lý này giúp học sinh giải quyết nhiều bài toán từ cơ bản đến nâng cao một cách hiệu quả.

Đề Bài

(Nội dung đề bài gốc từ video YouTube, được trích xuất và định dạng lại)

Cho hình thang ABCD với AB song song CD. Gọi O là giao điểm của hai đường chéo AC và BD.
a) Chứng minh rằng: $OA \cdot OD = OB \cdot OC$
b) Chứng minh rằng: $OA \cdot OD = OB \cdot OC$ (Lặp lại yêu cầu, giả định là ý khác hoặc lỗi trong bản ghi)
c) Nếu $AB = 6$ cm, $CD = 10$ cm, $AC = 8$ cm, tính độ dài OA và OC.

Phân Tích Yêu Cầu

Đề bài yêu cầu chứng minh hai đẳng thức liên quan đến tích các đoạn thẳng tạo bởi giao điểm của hai đường chéo trong hình thang, và sau đó áp dụng để tính độ dài các đoạn thẳng cụ thể khi biết độ dài một số đoạn khác.

Phần a) và b): Yêu cầu chứng minh $OA \cdot OD = OB \cdot OC$ . Cần sử dụng các tam giác đồng dạng để thiết lập tỉ lệ và suy ra đẳng thức này.
Phần c): Dựa vào kết quả đã chứng minh và tính chất của hình thang, ta sẽ thiết lập tỉ lệ giữa các đoạn thẳng trên đường chéo AC và BD, từ đó tìm ra OA và OC.

Kiến Thức/Nền Tảng Cần Dùng

Để giải quyết bài toán này, chúng ta cần nắm vững các kiến thức sau:

Định nghĩa hình thang: Hình thang là tứ giác có hai cạnh đối song song. Trong bài này, ABCD là hình thang với $AB parallel CD$.
Các trường hợp đồng dạng của tam giác:
- Trường hợp cạnh – góc – cạnh (c.g.c): Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc xen giữa bằng nhau, thì hai tam giác đồng dạng.
- Trường hợp góc – góc (g.g): Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia, thì hai tam giác đồng dạng.
Tính chất của hai tam giác đồng dạng: Các cạnh tương ứng tỉ lệ, các góc tương ứng bằng nhau.
Định lý Talet: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại tại hai điểm phân biệt, thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
Định lý Talet đảo và hệ quả: Đây là công cụ chính để chứng minh sự song song.

Cụ thể, chúng ta sẽ sử dụng tính chất hai tam giác đồng dạng để chứng minh các tỉ lệ cạnh, từ đó suy ra định lý Talet đảo.

Hướng Dẫn Giải Chi Tiết

Phần a) và b): Chứng minh $OA \cdot OD = OB \cdot OC$

Để chứng minh đẳng thức này, chúng ta sẽ xem xét các tam giác tạo bởi giao điểm O và các đỉnh của hình thang.

Xét tam giác OAB và tam giác OCD:

Vì $AB parallel CD$, ta có:
- Góc OAB = Góc OCD (so le trong)
- Góc OBA = Góc ODC (so le trong)
- Góc AOB = Góc COD (đối đỉnh)
Theo trường hợp đồng dạng góc – góc (g.g), ta suy ra:
$triangle OAB sim triangle OCD$
Từ sự đồng dạng này, ta có tỉ lệ các cạnh tương ứng:
$\frac{OA}{OC} = \frac{OB}{OD} = \frac{AB}{CD}$
Từ tỉ lệ $\frac{OA}{OC} = \frac{OB}{OD}$ , ta nhân chéo hai vế để có được đẳng thức cần chứng minh:
$OA \cdot OD = OB \cdot OC</code> (Đây chính là hệ quả của định lý Talet đảo khi áp dụng cho trường hợp cắt nhau của hai đường chéo trong hình thang) </li> </ul> Mẹo kiểm tra: Đẳng thức này luôn đúng cho mọi hình thang khi hai đường chéo cắt nhau. Nó thể hiện mối liên hệ về tỉ lệ giữa các đoạn thẳng trên đường chéo. Lỗi hay gặp: Học sinh thường nhầm lẫn tỉ lệ cạnh khi suy ra từ tam giác đồng dạng, hoặc quên mất điều kiện song song ($AB parallel CD$) là cốt lõi để có các cặp góc bằng nhau. <h3>Phần c) Tính độ dài OA và OC</h3> Chúng ta đã biết: <ul> <li>[]AB = 6$ cm
$CD = 10$ cm
$AC = 8$ cm

Và ta có tỉ lệ từ phần a) và b):
$\frac{OA}{OC} = \frac{AB}{CD}</code> Thay số vào, ta được: <code>[]\frac{OA}{OC} = \frac{6}{10} = \frac{3}{5}</code> Điều này có nghĩa là tỉ lệ giữa OA và OC là 3:5. Ngoài ra, ta biết rằng OA và OC là hai đoạn thẳng tạo nên đường chéo AC, nên: []OA + OC = AC$ $OA + OC = 8$ cm

Bây giờ, chúng ta có một hệ hai phương trình với hai ẩn OA và OC:

$\frac{OA}{OC} = \frac{3}{5}</code> => []5 \cdot OA = 3 \cdot OC$ => $OA = \frac{3}{5} \cdot OC$
$OA + OC = 8$

Thay phương trình (1) vào phương trình (2):
$(\frac{3}{5} \cdot OC) + OC = 8</code> <code>[](\frac{3}{5} + 1) \cdot OC = 8</code> <code>[]\frac{8}{5} \cdot OC = 8</code> Giải cho OC: <code>[]OC = 8 \cdot \frac{5}{8}</code> <code>[]OC = 5</code> cm Bây giờ, thay giá trị OC vào phương trình []OA + OC = 8$ : $OA + 5 = 8$ $OA = 8 - 5$ $OA = 3$ cm

Mẹo kiểm tra:

Kiểm tra lại tỉ lệ: $\frac{OA}{OC} = \frac{3}{5}$ , đúng với $\frac{AB}{CD} = \frac{6}{10} = \frac{3}{5}$ .
Kiểm tra tổng: $OA + OC = 3 + 5 = 8$ cm, đúng với độ dài AC.

Lỗi hay gặp: Sai sót trong việc thiết lập tỉ lệ hoặc giải hệ phương trình. Một số học sinh có thể gặp khó khăn trong việc sử dụng tỉ lệ để chia một đoạn thẳng thành các phần theo tỉ lệ cho trước.

Đáp Án/Kết Quả

a) và b) Chứng minh: $OA \cdot OD = OB \cdot OC$ dựa trên sự đồng dạng của $triangle OAB$ và $triangle OCD$.
c) Kết quả tính toán: $OA = 3$ cm và $OC = 5$ cm.

Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.