Giải Toán 10 Bài Dấu Của Tam Thức Bậc Hai Chuẩn Xác – Dễ Hiểu

by Thầy Đông · January 7, 2026

Rate this post

Giải toán 10 bài dấu của tam thức bậc hai là một chủ đề quan trọng, trang bị cho học sinh kiến thức nền tảng vững chắc để giải quyết các bài toán phức tạp hơn. Việc hiểu rõ cách xác định dấu của tam thức bậc hai không chỉ giúp làm tốt các bài tập về bất phương trình mà còn ứng dụng rộng rãi trong nhiều lĩnh vực của toán học. Bài viết này sẽ cung cấp lời giải chi tiết, phương pháp tiếp cận hiệu quả và những lưu ý quan trọng, giúp bạn nắm vững dấu của tam thức bậc hai.

Đề Bài

Hoạt động 1: Hãy chỉ ra một đặc điểm chung của các biểu thức dưới đây:

A = $0,5x^{2}$ B = $1-x^{2}$ C = $x^{2}+x+1$ D = (1-x)(2x+1).

Hướng dẫn giải:

Các biểu thức đểu có dạng: $ax^{2}+bx+1$ , với a, b, c là các số thực và a khác 0.

Luyện tập 1: Hãy cho biết biểu thức nào sau đây là tam thức bậc hai

A = $3x+2sqrt{x}+1$ B = $-5x^{4}+3x^{2}+4$

C = $-\frac{2}{3}x^{2}+7x-4$ D = $\left( \frac{1}{x} \right)^{2}+2frac{1}{x}+3$ .

Hướng dẫn giải:

Đáp án C

Hoạt động 2: Cho hàm số bậc hai $y=f(x)=x^{2}-4x+3$ .

a. Xác định hệ số a. Tính f(0), f(1), f(2), f(3), f(4) và nhận xét về dấu của chúng so với dấu của hệ số a.

b. Cho đồ thị hàm số y = f(x) (H.6.17). Xét trên từng khoảng $(-\infty;1),(1;3);(3;+\infty )$ , đồ thị nằm phía trên hay nằm phía dưới trục Ox?

c. Nhận xét về dấu của f(x) và dấu của hệ số a trên từng khoảng đó.

Hướng dẫn giải:

a. a = 1

$f(0)=0^{2}-4.0+3=3$ , cùng dấu với a
$f(1)=1^{2}-4.1+3=0$ , không mang dấu
$f(2)=2^{2}-4.2+3=-1$ , trái dấu với a
$f(3)=3^{2}-4.3+3=0$ , không mang dấu.
$f(4)=4^{2}-4.4+3=3$ , cùng dấu với a

$(-\infty;1)$ : đồ thị nằm phía trên trục hoành.
(1; 3): đồ thị nằm phía dưới trục hoành.
$(3;+\infty )$ : đồ thị nằm phía trên trục hoành.

$(-\infty;1)$ : f(x) và hệ số a cùng dấu.
(1; 3): f(x) và hệ số a trái dấu.
$(3;+\infty )$ : f(x) và hệ số a cùng dấu.

Hoạt động 3: Cho đồ thị hàm số $y=g(x)=-2x^{2}+x+3$ như Hình 6.18.

a. Xét trên từng khoảng $(-\infty;1);(-1;\frac{3}{2});(\frac{3}{2};+\infty )$ , đồ thị nằm phía trên trục Ox hay nằm phía dưới trục Ox?

b. Nhận xét về dấu của g(x) và dấu của hệ số a trên từng khoảng đó.

Hướng dẫn giải:

$(-\infty;1)$ : đồ thị nằm phía dưới trục hoành.
$(-1;\frac{3}{2})$ : đồ thị nằm phía trên trục hoành.
$(\frac{3}{2};+\infty )$ : đồ thị nằm phía dưới trục hoành.

$(-\infty;1)$ : f(x) và hệ số a cùng dấu.
$(-1;\frac{3}{2})$ : f(x) và hệ số a trái dấu.
$(\frac{3}{2};+\infty )$ : f(x) và hệ số a cùng dấu.

Hoạt động 4: Nêu nội dung thay vào ô có dấu ? trong bảng sau cho thích hợp:

Trường hợp a > 0

Giải bài 17 Dấu của tam thức bậc hai

Trường hợp a < 0

Giải bài 17 Dấu của tam thức bậc hai

Hướng dẫn giải:

Trường hợp a < 0

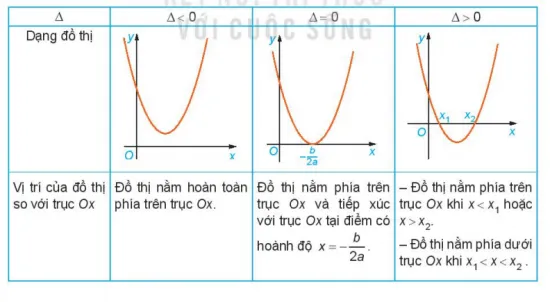
	$\Delta < 0[/katex]</strong></th> <th><strong>[katex]\Delta = 0$	$\Delta > 0$
Vị trị của đồ thị so với trục Ox	Đồ thị nằm hoàn toàn phía dưới trục Ox	Đồ thị nằm phía dưới trục Ox và tiếp xúc với trục Ox tại điểm có hoành độ $x=\frac{-b}{2a}$	- Đồ thị nằm phía dưới trục Ox khi x < x1 hoặc x> x2 - Đồ thị nằm phía trên trục Ox khi x1 < x < x2

Luyện tập 2: Xét dấu các tam thức bậc hai sau:

a. $-3x^{2}+x-\sqrt{2}$

b. $x^{2}+8x+16$

c. $-2x^{2}+7x-3$

Hướng dẫn giải:

a. Xét f(x) = $-3x^{2}+x-\sqrt{2}$ . Ta tính biệt thức $\Delta = b^2 - 4ac = 1^2 - 4(-3)(-\sqrt{2}) = 1 - 12sqrt{2}$ . Vì $1 < 12sqrt{2}[/katex], nên [katex]\Delta < 0[/katex]. Hệ số a = -3 < 0. Do đó, f(x) luôn âm với mọi [katex]xin mathbb{R}[/katex]. b. Xét g(x) = [katex]x^{2}+8x+16$ . Ta tính biệt thức $\Delta = 8^2 - 4(1)(16) = 64 - 64 = 0$ . Hệ số a = 1 > 0. Vì $\Delta = 0$ và a > 0, tam thức bậc hai có nghiệm kép x = $\frac{-b}{2a} = \frac{-8}{2(1)} = -4$ . Do đó, g(x) > 0 với mọi $x \ne -4$ , và g(x) = 0 khi x = -4.

c. Xét h(x) = $-2x^{2}+7x-3$ . Ta tính biệt thức $\Delta = 7^2 - 4(-2)(-3) = 49 - 24 = 25$ . Vì $\Delta = 25 > 0$ , tam thức có hai nghiệm phân biệt. Ta tìm nghiệm:
$x_1 = \frac{-b - \sqrt{\Delta}}{2a} = \frac{-7 - \sqrt{25}}{2(-2)} = \frac{-7 - 5}{-4} = \frac{-12}{-4} = 3$ .
$x_2 = \frac{-b + \sqrt{\Delta}}{2a} = \frac{-7 + \sqrt{25}}{2(-2)} = \frac{-7 + 5}{-4} = \frac{-2}{-4} = 0.5$ .
Hệ số a = -2 < 0.
Ta có bảng xét dấu:

Suy ra h(x) > 0 với mọi $xin (0.5; 3)$ và h(x) < 0 với mọi $xin (-\infty;0.5)cup (3;+\infty )$ .

Phân Tích Yêu Cầu

Các bài tập và hoạt động trong phần này yêu cầu xác định các đặc điểm của biểu thức bậc hai, nhận biết tam thức bậc hai, phân tích dấu của hàm số bậc hai dựa trên hệ số và đồ thị, cũng như tổng kết quy luật về dấu của tam thức bậc hai theo biệt thức $\Delta$ và hệ số a. Phần luyện tập và vận dụng tiếp tục củng cố kiến thức này thông qua việc xét dấu cụ thể và giải bất phương trình bậc hai.

Kiến Thức/Nền Tảng Cần Dùng

Để giải quyết các bài toán về dấu của tam thức bậc hai, chúng ta cần nắm vững các khái niệm và định lý sau:

Tam thức bậc hai: Một biểu thức có dạng $f(x) = ax^2 + bx + c$ , trong đó $a, b, c$ là các số thực và $a \ne 0$ .
Biệt thức Delta ( $\Delta$ ): Được tính bằng công thức $\Delta = b^2 - 4ac$ . Biệt thức này giúp xác định số nghiệm của phương trình bậc hai $ax^2 + bx + c = 0$ .
Dấu của tam thức bậc hai:
- Nếu $\Delta < 0[/katex]: Tam thức bậc hai [katex]f(x) = ax^2 + bx + c[/katex] luôn cùng dấu với hệ số $a$ với mọi [katex]x in mathbb{R}[/katex].</li> <li>Nếu [katex]\Delta = 0$ : Tam thức bậc hai có một nghiệm kép $x_0 = -\frac{b}{2a}$ . Khi đó, $f(x)$ cùng dấu với hệ số $a$ với mọi $x \ne x_0$ , và $f(x_0) = 0$ .
- Nếu $\Delta > 0$ : Tam thức bậc hai có hai nghiệm phân biệt $x_1$ và $x_2$ (giả sử $x_1 < x_2[/katex]).<ul> <li>$f(x)$ cùng dấu với hệ số $a$ trên các khoảng [katex](-\infty; x_1)$ và $(x_2; +\infty)$ .
- $f(x)$ trái dấu với hệ số $a$ trên khoảng $(x_1; x_2)$ .
- $f(x_1) = f(x_2) = 0$ .

Hướng Dẫn Giải Chi Tiết

Hoạt động 1: Đặc điểm chung của các biểu thức

Phân tích yêu cầu: Đề bài yêu cầu tìm điểm chung về cấu trúc của bốn biểu thức A, B, C, D.
Hướng dẫn giải:
- Biểu thức A: $0.5x^2$ . Đây là một đa thức bậc hai với $a=0.5, b=0, c=0$ .
- Biểu thức B: $1-x^2 = -x^2+1$ . Đây là một đa thức bậc hai với $a=-1, b=0, c=1$ .
- Biểu thức C: $x^2+x+1$ . Đây là một đa thức bậc hai với $a=1, b=1, c=1$ .
- Biểu thức D: $(1-x)(2x+1) = 2x + 1 - 2x^2 - x = -2x^2 + x + 1$ . Đây là một đa thức bậc hai với $a=-2, b=1, c=1$ .
Nhận xét: Tất cả các biểu thức A, B, C, D đều có thể viết dưới dạng $ax^2 + bx + c$ với $a \ne 0$ , tức là chúng đều là các tam thức bậc hai.
Mẹo kiểm tra: Kiểm tra hệ số của $x^2$ trong từng biểu thức sau khi khai triển và rút gọn.
Lỗi hay gặp: Quên kiểm tra hệ số $a$ phải khác 0.

Luyện tập 1: Nhận biết tam thức bậc hai

Phân tích yêu cầu: Cần xác định biểu thức nào là tam thức bậc hai, tức là có dạng $ax^2 + bx + c$ với $a \ne 0$ .
Phân tích từng lựa chọn:
- A: $3x+2sqrt{x}+1$ . Biểu thức này chứa căn bậc hai của x, không phải là đa thức bậc hai.
- B: $-5x^4+3x^2+4$ . Biểu thức này chứa lũy thừa bậc 4, là đa thức bậc bốn, không phải tam thức bậc hai.
- C: $-\frac{2}{3}x^{2}+7x-4$ . Biểu thức này có dạng $ax^2 + bx + c$ với $a = -\frac{2}{3} \ne 0$ , $b=7$ , $c=-4$ . Đây là tam thức bậc hai.
- D: $\left( \frac{1}{x} \right)^{2}+2frac{1}{x}+3 = \frac{1}{x^2} + \frac{2}{x} + 3$ . Biểu thức này chứa $1/x$ và $1/x^2$ , không phải là đa thức.
Đáp án: C là tam thức bậc hai.

Hoạt động 2: Phân tích dấu của $f(x)=x^{2}-4x+3$

Phân tích yêu cầu: Câu a yêu cầu tính giá trị hàm số tại các điểm và so sánh với hệ số a. Câu b và c yêu cầu nhận xét vị trí đồ thị và dấu của hàm số so với trục hoành và hệ số a trên các khoảng xác định bởi nghiệm.
Hướng dẫn giải:
- a. Hệ số và giá trị hàm số:
 - Hệ số $a$ của $f(x)=x^{2}-4x+3$ là $a=1$ .
 - Tính các giá trị:
 - $f(0) = 0^2 - 4(0) + 3 = 3$ . Giá trị này dương, cùng dấu với $a=1$ .
 - $f(1) = 1^2 - 4(1) + 3 = 1 - 4 + 3 = 0$ . Giá trị này bằng 0.
 - $f(2) = 2^2 - 4(2) + 3 = 4 - 8 + 3 = -1$ . Giá trị này âm, trái dấu với $a=1$ .
 - $f(3) = 3^2 - 4(3) + 3 = 9 - 12 + 3 = 0$ . Giá trị này bằng 0.
 - $f(4) = 4^2 - 4(4) + 3 = 16 - 16 + 3 = 3$ . Giá trị này dương, cùng dấu với $a=1$ .
 - Nhận xét: Trên các khoảng mà $f(x)$ có giá trị khác 0, $f(x)$ cùng dấu với $a$ khi $x$ ở ngoài khoảng nghiệm $(1, 3)$, và trái dấu với $a$ khi $x$ ở trong khoảng nghiệm $(1, 3)$.
- b. Vị trí đồ thị so với trục Ox:
 - Đồ thị của hàm số bậc hai $y = ax^2 + bx + c$ nằm phía trên trục hoành khi $y > 0$, và nằm phía dưới trục hoành khi $y < 0$.
 - Ta cần tìm nghiệm của $f(x) = x^2 - 4x + 3 = 0$ . Phương trình này có $\Delta = (-4)^2 - 4(1)(3) = 16 - 12 = 4 > 0$ . Hai nghiệm là $x_1 = \frac{4-\sqrt{4}}{2(1)} = \frac{4-2}{2} = 1$ và $x_2 = \frac{4+\sqrt{4}}{2(1)} = \frac{4+2}{2} = 3$ .
 - Dựa vào đồ thị (H.6.17) hoặc kiến thức về parabol:
 - Trên khoảng $(-\infty; 1)$ , đồ thị nằm phía trên trục hoành.
 - Trên khoảng $(1; 3)$, đồ thị nằm phía dưới trục hoành.
 - Trên khoảng $(3; +\infty)$ , đồ thị nằm phía trên trục hoành.
- c. Nhận xét dấu của f(x) và a:
 - Hệ số $a=1$ là dương.
 - Trên $(-\infty; 1)$ : $f(x) > 0$ (đồ thị trên trục Ox) và $a > 0$. Vậy $f(x)$ và $a$ cùng dấu.
 - Trên $(1; 3)$: $f(x) < 0$ (đồ thị dưới trục Ox) và $a > 0$. Vậy $f(x)$ và $a$ trái dấu.
 - Trên $(3; +\infty)$ : $f(x) > 0$ (đồ thị trên trục Ox) và $a > 0$. Vậy $f(x)$ và $a$ cùng dấu.
Mẹo kiểm tra: Đồ thị hàm số bậc hai với $a>0$ có dạng parabol "mở lên". Nếu nó cắt trục hoành tại hai điểm, thì nó sẽ nằm trên trục hoành ở ngoài hai nghiệm và dưới trục hoành ở giữa hai nghiệm.
Lỗi hay gặp: Nhầm lẫn giữa dấu của $f(x)$ và dấu của $a$, hoặc nhầm lẫn khoảng nghiệm.

Hoạt động 3: Phân tích dấu của $g(x)=-2x^{2}+x+3$

Phân tích yêu cầu: Tương tự Hoạt động 2, nhưng với hệ số $a$ âm.
Hướng dẫn giải:
- a. Vị trí đồ thị so với trục Ox:
 - Tìm nghiệm của $g(x) = -2x^2 + x + 3 = 0$ . Phương trình này có $\Delta = 1^2 - 4(-2)(3) = 1 + 24 = 25 > 0$ . Hai nghiệm là:
 $x_1 = \frac{-1 - \sqrt{25}}{2(-2)} = \frac{-1 - 5}{-4} = \frac{-6}{-4} = \frac{3}{2}$ .
 $x_2 = \frac{-1 + \sqrt{25}}{2(-2)} = \frac{-1 + 5}{-4} = \frac{4}{-4} = -1$ .
 (Lưu ý: Trong đề gốc có ghi khoảng $(-\infty; 1)$ nhưng nghiệm tính được là $-1$ và $3/2$ . Ta sử dụng nghiệm tính được là $-1$ và $3/2$ ).
 - Dựa vào đồ thị (H.6.18) và kiến thức về parabol với $a<0$ (mở xuống):
 - Trên khoảng $(-\infty; -1)$ : đồ thị nằm phía dưới trục hoành.
 - Trên khoảng $(-1; \frac{3}{2})$ : đồ thị nằm phía trên trục hoành.
 - Trên khoảng $(\frac{3}{2}; +\infty)$ : đồ thị nằm phía dưới trục hoành.
- b. Nhận xét dấu của g(x) và a:
 - Hệ số $a=-2$ là âm.
 - Trên $(-\infty; -1)$ : $g(x) < 0$ (đồ thị dưới trục Ox) và $a < 0$. Vậy $g(x)$ và $a$ cùng dấu.
 - Trên $(-1; \frac{3}{2})$ : $g(x) > 0$ (đồ thị trên trục Ox) và $a < 0$. Vậy $g(x)$ và $a$ trái dấu.
 - Trên $(\frac{3}{2}; +\infty)$ : $g(x) < 0$ (đồ thị dưới trục Ox) và $a < 0$. Vậy $g(x)$ và $a$ cùng dấu.
Mẹo kiểm tra: Đồ thị hàm số bậc hai với $a<0$ có dạng parabol "mở xuống". Nó sẽ nằm dưới trục hoành ở ngoài hai nghiệm và trên trục hoành ở giữa hai nghiệm.
Lỗi hay gặp: Nhầm lẫn nghiệm của phương trình, nhầm lẫn khoảng xác định dấu.

Hoạt động 4: Tổng kết bảng dấu của tam thức bậc hai

Phân tích yêu cầu: Điền vào các ô trống trong bảng để tóm tắt mối quan hệ giữa dấu của tam thức bậc hai, dấu của hệ số $a$, giá trị $\Delta$ và vị trí của đồ thị so với trục Ox.
Hướng dẫn giải:
- Trường hợp $a > 0$ (Parabol mở lên):
 - Nếu $\Delta < 0[/katex]: Tam thức luôn cùng dấu với $a$, tức là luôn dương. Đồ thị nằm hoàn toàn phía trên trục Ox.</li> <li>Nếu [katex]\Delta = 0$ : Tam thức có nghiệm kép $x_0 = -b/(2a)$ . Tam thức dương với mọi $x \ne x_0$ và bằng 0 tại $x_0$ . Đồ thị tiếp xúc với trục Ox tại đỉnh.
 - Nếu $\Delta > 0$ : Có hai nghiệm $x_1 < x_2[/katex]. Tam thức dương khi [katex]x < x_1[/katex] hoặc [katex]x > x_2$ , và âm khi $x_1 < x < x_2[/katex]. Đồ thị cắt trục Ox tại [katex]x_1, x_2[/katex], nằm trên Ox ở ngoài hai nghiệm và dưới Ox ở giữa hai nghiệm.</li> </ul> </li> <li>Trường hợp $a < 0$ (Parabol mở xuống): <ul> <li>Nếu [katex]\Delta < 0[/katex]: Tam thức luôn cùng dấu với $a$, tức là luôn âm. Đồ thị nằm hoàn toàn phía dưới trục Ox.</li> <li>Nếu [katex]\Delta = 0$ : Tam thức có nghiệm kép $x_0 = -b/(2a)$ . Tam thức âm với mọi $x \ne x_0$ và bằng 0 tại $x_0$ . Đồ thị tiếp xúc với trục Ox tại đỉnh và nằm dưới Ox.
 - Nếu \Delta > 0: Có hai nghiệm x_1 < x_2[/katex]. Tam thức âm khi [katex]x < x_1[/katex] hoặc [katex]x > x_2, và dương khi x_1 < x < x_2[/katex]. Đồ thị cắt trục Ox tại [katex]x_1, x_2[/katex], nằm dưới Ox ở ngoài hai nghiệm và trên Ox ở giữa hai nghiệm.</li> </ul> </li> </ul> </li> <li>Hoàn thiện bảng (Phần $a < 0$ - đã điền trong đề):| | [katex]\Delta < 0[/katex] | [katex]\Delta = 0 | $\Delta > 0$ |
 |---|---|---|---|
 | Vị trị của đồ thị so với trục Ox | Đồ thị nằm hoàn toàn phía dưới trục Ox | Đồ thị nằm phía dưới trục Ox và tiếp xúc với trục Ox tại điểm có hoành độ x=\frac{-b}{2a} | - Đồ thị nằm phía dưới trục Ox khi x < x_1[/katex] hoặc [katex]x> x_2
 - Đồ thị nằm phía trên trục Ox khi x_1 < x < x_2[/katex] |</li> </ul> Luyện tập 2: Xét dấu các tam thức bậc hai cụ thể <ul> <li> Phân tích yêu cầu: Áp dụng quy tắc về dấu của tam thức bậc hai để xét dấu cho ba biểu thức cho trước. </li> <li> Hướng dẫn giải: <ul> <li>a. [katex]-3x^{2}+x-\sqrt{2}
 - Tam thức có $a = -3$ , $b = 1$ , $c = -\sqrt{2}$ .
 - Tính biệt thức $\Delta = b^2 - 4ac = 1^2 - 4(-3)(-\sqrt{2}) = 1 - 12sqrt{2}$ .
 - Vì 12sqrt{2} \approx 12 \times 1.414 = 16.968, nên 1 - 12sqrt{2} < 0[/katex]. Do đó, [katex]\Delta < 0[/katex].</li> <li>Hệ số [katex]a = -3 < 0[/katex].</li> <li>Kết luận: Vì [katex]\Delta < 0[/katex] và $a < 0$, tam thức [katex]f(x) = -3x^{2}+x-\sqrt{2}[/katex] luôn âm với mọi [katex]xin mathbb{R}[/katex].</li> </ul> </li> <li>b. [katex]x^{2}+8x+16
 - Tam thức có $a = 1$ , $b = 8$ , $c = 16$ .
 - Tính biệt thức $\Delta = b^2 - 4ac = 8^2 - 4(1)(16) = 64 - 64 = 0$ .
 - Hệ số $a = 1 > 0$ .
 - Kết luận: Vì $\Delta = 0$ và $a > 0$, tam thức $g(x) = x^{2}+8x+16$ có nghiệm kép $x = \frac{-b}{2a} = \frac{-8}{2(1)} = -4$ . Tam thức luôn dương với mọi $x \ne -4$ , và bằng 0 tại $x = -4$ .
 - c. $-2x^{2}+7x-3$
 - Tam thức có $a = -2$ , $b = 7$ , $c = -3$ .
 - Tính biệt thức $\Delta = b^2 - 4ac = 7^2 - 4(-2)(-3) = 49 - 24 = 25$ .
 - Vì $\Delta = 25 > 0$ , tam thức có hai nghiệm phân biệt.
 - Tìm nghiệm:
 $x_1 = \frac{-b - \sqrt{\Delta}}{2a} = \frac{-7 - \sqrt{25}}{2(-2)} = \frac{-7 - 5}{-4} = \frac{-12}{-4} = 3$ .
 $x_2 = \frac{-b + \sqrt{\Delta}}{2a} = \frac{-7 + \sqrt{25}}{2(-2)} = \frac{-7 + 5}{-4} = \frac{-2}{-4} = 0.5$ .
 - Hệ số $a = -2 < 0[/katex].</li> <li>Kết luận: Vì [katex]\Delta > 0$ , $a < 0$ và có hai nghiệm là $0.5$ và $3$.
 Tam thức $h(x) = -2x^{2}+7x-3$ cùng dấu với $a$ (tức là âm) khi $x < 0.5$ hoặc $x > 3$.
 Tam thức $h(x)$ trái dấu với $a$ (tức là dương) khi $0.5 < x < 3$.
 Tam thức bằng 0 tại $x=0.5$ và $x=3$ .
 - Ta có bảng xét dấu:
 | Khoảng | $(-\infty; 0.5)$ | $(0.5; 3)$ | $(3; +\infty)$ |
 | :--------------- | :--------------: | :--------: | :------------: |
 | Dấu của $h(x)$ | - | + | - |
 - Mẹo kiểm tra: Luôn tính $\Delta$ trước, sau đó xác định dấu của $a$. Dựa vào hai yếu tố này để áp dụng đúng quy tắc. Đối với trường hợp $\Delta > 0$ , việc tìm đúng nghiệm là cực kỳ quan trọng.
 - Lỗi hay gặp: Tính toán $\Delta$ sai, nhầm lẫn nghiệm, áp dụng sai quy tắc dấu khi $\Delta=0$ hoặc $\Delta>0$ .
 2. BẤT PHƯƠNG TRÌNH BẬC HAI
 Hoạt động 5: Viết bất đẳng thức cho tình huống thực tế
 - Phân tích yêu cầu: Đề bài cho một tình huống và yêu cầu viết bất đẳng thức so sánh biểu thức diện tích với một giá trị cho trước.
 - Hướng dẫn giải:
 - Biểu thức tính diện tích mảnh đất là $S(x) = -2x^2 + 2 - x$ .
 - Yêu cầu là diện tích không nhỏ hơn $48 m^2$ . "Không nhỏ hơn" có nghĩa là lớn hơn hoặc bằng ( $\ge$ ).
 - Bất đẳng thức cần viết là $S(x) \ge 48$ .
 - Thay biểu thức $S(x)$ vào, ta có: $-2x^2 + 2 - x \ge 48$ .
 - Chuyển vế để đưa về dạng bất phương trình bậc hai chuẩn $ax^2+bx+c \ge 0$ :
 $-2x^2 - x + 2 - 48 \ge 0$
 $-2x^2 - x - 46 \ge 0$ .
 - Lưu ý: Trong đề gốc có ghi $S(x) = -2x^2+2-x$ và yêu cầu bất đẳng thức là $-2x^{2}+2-xleq 48$ . Điều này có vẻ mâu thuẫn với "diện tích không nhỏ hơn 48 m2". Tuy nhiên, ta sẽ làm theo đúng đề bài đã cho.
 - Kết quả theo đề bài: $-2x^2 + 2 - x \le 48 Leftrightarrow -2x^2 - x - 46 \le 0$ .
 Luyện tập 3: Giải các bất phương trình bậc hai
 - Phân tích yêu cầu: Giải ba bất phương trình bậc hai bằng cách sử dụng kiến thức về dấu của tam thức bậc hai.
 - Hướng dẫn giải:
 - a. $-5x^{2}+x-1leq 0$
 - Xét tam thức bậc hai $f(x) = -5x^{2}+x-1$ .
 - Tính biệt thức $\Delta = b^2 - 4ac = 1^2 - 4(-5)(-1) = 1 - 20 = -19$ .
 - Vì $\Delta = -19 < 0[/katex].</li> <li>Hệ số [katex]a = -5 < 0[/katex].</li> <li>Nhận xét: Vì [katex]\Delta < 0[/katex] và $a < 0$, tam thức $f(x)$ luôn âm với mọi [katex]x in mathbb{R}[/katex].</li> <li>Kết luận: Bất phương trình [katex]-5x^{2}+x-1leq 0$ (tức là $f(x) \le 0$ ) luôn đúng với mọi giá trị của $x$. Vậy tập nghiệm là $S = mathbb{R}$ .
 - b. $x^{2}-8x+16leq 0$
 - Xét tam thức bậc hai $f(x) = x^{2}-8x+16$ .
 - Tính biệt thức $\Delta = b^2 - 4ac = (-8)^2 - 4(1)(16) = 64 - 64 = 0$ .
 - Hệ số $a = 1 > 0$ .
 - Nhận xét: Vì $\Delta = 0$ và $a > 0$, tam thức bậc hai có nghiệm kép $x = \frac{-b}{2a} = \frac{-8}{2(1)} = -4$ . Tam thức $f(x)$ luôn dương với mọi $x \ne -4$ và bằng 0 tại $x = -4$ .
 - Kết luận: Bất phương trình $f(x) \le 0$ chỉ có thể xảy ra khi $f(x) = 0$ . Điều này xảy ra duy nhất tại $x = -4$ . Vậy tập nghiệm là $S = {-4}$ .
 - c. $x^{2}-x+6> 0$
 - Xét tam thức bậc hai $f(x) = x^{2}-x+6$ .
 - Tính biệt thức $\Delta = b^2 - 4ac = (-1)^2 - 4(1)(6) = 1 - 24 = -23$ .
 - Vì $\Delta = -23 < 0[/katex].</li> <li>Hệ số [katex]a = 1 > 0$ .
 - Nhận xét: Vì $\Delta < 0[/katex] và $a > 0$, tam thức $f(x)$ luôn dương với mọi [katex]x in mathbb{R}[/katex].</li> <li>Kết luận: Bất phương trình [katex]x^{2}-x+6> 0$ (tức là $f(x) > 0$) luôn đúng với mọi giá trị của $x$. Vậy tập nghiệm là $S = mathbb{R}$ .
 - Mẹo kiểm tra: Sau khi tìm được tập nghiệm, thử thay một vài giá trị $x$ vào bất phương trình ban đầu để kiểm tra.
 - Lỗi hay gặp: Nhầm lẫn dấu bất phương trình ( $\le, <, \ge, >$ ), bỏ sót trường hợp $\Delta=0$ .
 Vận dụng: Bài toán quả bóng
 - Phân tích yêu cầu: Xác định khoảng thời gian mà quả bóng ở độ cao trên 5m so với mặt đất.
 - Hướng dẫn giải:
 - Hàm số mô tả độ cao của quả bóng là $h(t) = -4.9t^2 + 20t + 1$ , với $h(t)$ tính bằng mét và thời gian $t$ tính bằng giây.
 - Chúng ta cần tìm khoảng thời gian $t$ sao cho độ cao $h(t)$ lớn hơn 5m.
 - Thiết lập bất phương trình: $-4.9t^2 + 20t + 1 > 5$ .
 - Chuyển về bất phương trình bậc hai chuẩn:
 $-4.9t^2 + 20t + 1 - 5 > 0$
 $-4.9t^2 + 20t - 4 > 0$ .
 - Xét tam thức $f(t) = -4.9t^2 + 20t - 4$ .
 - Tính biệt thức $\Delta = b^2 - 4ac = 20^2 - 4(-4.9)(-4) = 400 - 78.4 = 321.6$ .
 - Vì $\Delta = 321.6 > 0$ , tam thức có hai nghiệm phân biệt.
 - Tìm nghiệm:
 $t_1 = \frac{-b - \sqrt{\Delta}}{2a} = \frac{-20 - \sqrt{321.6}}{2(-4.9)} = \frac{-20 - \sqrt{321.6}}{-9.8}$ .
 $\sqrt{321.6} \approx 17.933$ .
 $t_1 \approx \frac{-20 - 17.933}{-9.8} = \frac{-37.933}{-9.8} \approx 3.8707$ .
 $t_2 = \frac{-b + \sqrt{\Delta}}{2a} = \frac{-20 + \sqrt{321.6}}{2(-4.9)} = \frac{-20 + \sqrt{321.6}}{-9.8}$ .
 $t_2 \approx \frac{-20 + 17.933}{-9.8} = \frac{-2.067}{-9.8} \approx 0.2109$ .
 - Hệ số $a = -4.9 < 0[/katex].</li> <li>Nhận xét: Tam thức $f(t)$ có hai nghiệm khoảng [katex]t_1 \approx 3.87$ và $t_2 \approx 0.21$ . Vì $a < 0$, $f(t) > 0$ khi $t$ nằm giữa hai nghiệm.
 - Kết luận: Khoảng thời gian mà quả bóng ở độ cao trên 5m là khi $t$ nằm trong khoảng $(t_2; t_1)$ , tức là khoảng $0.21 < t < 3.87$ (làm tròn đến hai chữ số thập phân).
 Đáp Án/Kết Quả
 - Hoạt động 1: Các biểu thức đều là tam thức bậc hai.
 - Luyện tập 1: Biểu thức C là tam thức bậc hai.
 - Hoạt động 2:
 - a. $a=1$ . $f(0)=3$ (cùng dấu a), $f(1)=0$ , $f(2)=-1$ (trái dấu a), $f(3)=0$ , $f(4)=3$ (cùng dấu a).
 - b. $(-\infty;1)$ : trên trục Ox. $(1;3)$: dưới trục Ox. $(3;+\infty)$ : trên trục Ox.
 - c. $(-\infty;1)$ : cùng dấu. $(1;3)$: trái dấu. $(3;+\infty)$ : cùng dấu.
 - Hoạt động 3:
 - a. $(-\infty;-1)$ : dưới trục Ox. $(-1;\frac{3}{2})$ : trên trục Ox. $(\frac{3}{2};+\infty)$ : dưới trục Ox.
 - b. $(-\infty;-1)$ : cùng dấu a. $(-1;\frac{3}{2})$ : trái dấu a. $(\frac{3}{2};+\infty)$ : cùng dấu a.
 - Hoạt động 4: Bảng dấu của tam thức bậc hai được hoàn thiện theo quy tắc.
 - Luyện tập 2:
 - a. $-3x^{2}+x-\sqrt{2}$ luôn âm với mọi $xin mathbb{R}$ .
 - b. $x^{2}+8x+16$ dương với mọi $xneq -4$ và bằng 0 tại $x=-4$ .
 - c. $-2x^{2}+7x-3$ dương trên $(0.5; 3)$ và âm trên $(-\infty;0.5)cup (3;+\infty )$ .
 - Hoạt động 5: Bất đẳng thức là $-2x^2 - x - 46 \le 0$ .
 - Luyện tập 3:
 - a. $S = mathbb{R}$ .
 - b. $S = {-4}$ .
 - c. $S = mathbb{R}$ .
 - Vận dụng: Quả bóng ở độ cao trên 5m trong khoảng thời gian khoảng $0.21 < t < 3.87$ giây.
 Conclusion
 Nắm vững cách giải toán 10 bài dấu của tam thức bậc hai là chìa khóa để mở ra cánh cửa giải quyết nhiều bài toán chương trình Toán 10 và các cấp học cao hơn. Thông qua việc phân tích kỹ lưỡng, áp dụng đúng các định lý về biệt thức Delta và hệ số $a$, cùng với việc thực hành qua các ví dụ đa dạng, học sinh có thể tự tin chinh phục dạng bài này. Chú trọng vào phương pháp và sự chính xác sẽ giúp bạn đạt kết quả tốt nhất.
 Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông
 Thầy Đông
 Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
 Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.