Giải Toán 10 trang 15 Tập 1 Chân trời sáng tạo

by Thầy Đông · January 9, 2026

Rate this post

Giải Toán 10 trang 15 Tập 1 thuộc Bài 1: Mệnh đề trong sách giáo khoa Toán 10 Chân trời sáng tạo là tài liệu hữu ích, cung cấp lời giải chi tiết và phương pháp làm bài chuẩn xác cho các em học sinh. Bài viết này sẽ đi sâu vào phân tích từng bài tập, giúp các em nắm vững kiến thức về mệnh đề, điều kiện cần, điều kiện đủ và các kí hiệu toán học.

Đề Bài

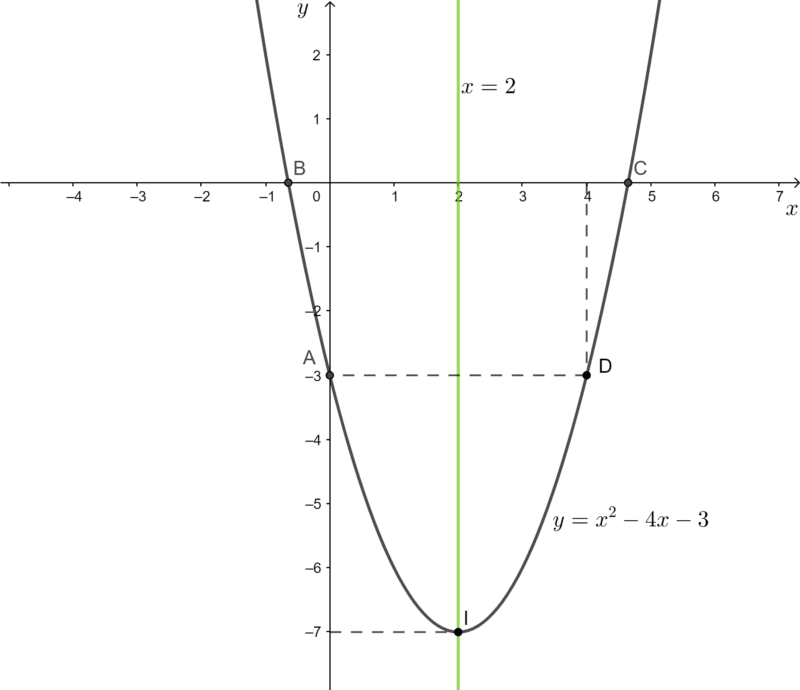
Bài 4 trang 15 Toán lớp 10 Tập 1: Cho các định lí:

P: “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”;

Q: “Nếu a < b thì a + c < b + c” (a, b, c ∈ ℝ).

a) Chỉ ra giả thiết và kết luận của mỗi định lí;

b) Phát biểu lại mỗi định lí đã cho, sử dụng thuật ngữ “điều kiện cần” hoặc “điều kiện đủ”.

c) Mệnh đề đảo của mỗi định lí đó có là định lí không?

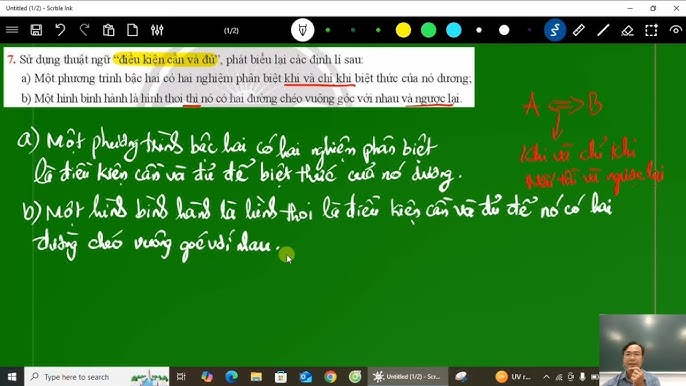
Bài 5 trang 15 Toán lớp 10 Tập 1: Sử dụng thuật ngữ “điều kiện cần và đủ”, phát biểu các định lí sau:

a) Một phương trình bậc hai có hai nghiệm phân biệt khi và chỉ khi biệt thức của nó dương;

b) Một hình bình hành là hình thoi thì nó có hai đường chéo vuông góc với nhau và ngược lại.

Bài 6 trang 15 Toán lớp 10 Tập 1: Cho các mệnh đề sau:

P: “Giá trị tuyệt đối của mọi số thực đều lớn hơn hoặc bằng chính nó”;

Q: “Có số tự nhiên sao cho bình phương của nó bằng 10”;

R: “Có số thực x sao cho x^2 + 2x – 1 = 0”.

a) Xét tính đúng sai của mỗi mệnh đề trên.

b) Sử dụng kí hiệu ∀, ∃ để viết lại các mệnh đề đã cho.

Bài 7 trang 15 Toán lớp 10 Tập 1: Xét tính đúng, sai và viết mệnh đề phủ định của các mệnh đề sau đây:

a) ∃x∈ℕ , x + 3 = 0;

b) ∀x ∈ ℝ , x^2 + 1 ≥ 2x;

c) ∀a∈ℝ,a^2=a.

Phân Tích Yêu Cầu

Các bài tập trang 15 thuộc chương Mệnh đề Toán học lớp 10 tập trung vào việc hiểu và áp dụng các khái niệm cơ bản như giả thiết, kết luận, mệnh đề đảo, điều kiện cần, điều kiện đủ và điều kiện cần và đủ. Học sinh cần phân biệt rõ vai trò của từng phần trong một định lí và cách diễn đạt chúng dưới các hình thức khác nhau. Ngoài ra, bài tập còn yêu cầu vận dụng các kí hiệu logic ∀ (với mọi) và ∃ (tồn tại) để viết lại các mệnh đề một cách chính xác.

Kiến Thức/Nền Tảng Cần Dùng

Để giải quyết các bài tập này, học sinh cần nắm vững các kiến thức sau:

Mệnh đề: Là câu khẳng định đúng hoặc sai.
Định lí: Là mệnh đề đúng. Một định lí thường có dạng P ⇒ Q, trong đó P là giả thiết, Q là kết luận.
Mệnh đề đảo: Là mệnh đề Q ⇒ P.
Điều kiện đủ: P là điều kiện đủ để có Q nếu P ⇒ Q là đúng.
Điều kiện cần: P là điều kiện cần để có Q nếu Q ⇒ P là đúng (tương đương với P ⇒ Q là đúng).
Điều kiện cần và đủ: P là điều kiện cần và đủ để có Q nếu P ⇔ Q là đúng (tương đương với cả P ⇒ Q và Q ⇒ P đều đúng).
Các kí hiệu logic:
- ∀ (với mọi): Dùng để khẳng định một tính chất đúng với mọi phần tử trong một tập hợp.
- ∃ (tồn tại): Dùng để khẳng định một tính chất đúng với ít nhất một phần tử trong một tập hợp.
- Mệnh đề phủ định.
Các phép toán với bất đẳng thức và phương trình: Cộng hai vế với cùng một số, nhân hai vế với một số dương, xác định nghiệm của phương trình bậc hai.

Các công thức toán học sẽ được sử dụng và trình bày dưới dạng KaTeX để đảm bảo tính chính xác.

Phân số: dfrac{a}{b}
Nhân: times hoặc cdot
Dấu lớn hơn hoặc bằng: ge
Dấu nhỏ hơn hoặc bằng: le
Dấu khác: ne
Biểu thức trong mệnh đề: x^2, a+c, b+c, a<b, a+c<b+c
Tập hợp số thực: mathbb{R}
Tập hợp số tự nhiên: mathbb{N}
Biệt thức: Delta hoặc Delta'
Kí hiệu lượng từ: forall, exists

Hướng Dẫn Giải Chi Tiết

Bài 4 trang 15 Toán lớp 10 Tập 1

a) Chỉ ra giả thiết và kết luận của mỗi định lí:

Định lí P: “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”.
- Giả thiết: Hai tam giác bằng nhau.
- Kết luận: Diện tích của chúng bằng nhau.
Định lí Q: “Nếu a < b thì a + c < b + c” (a, b, c ∈ ℝ).
- Giả thiết: a < b.
- Kết luận: a + c < b + c.

b) Phát biểu lại mỗi định lí đã cho, sử dụng thuật ngữ “điều kiện cần” hoặc “điều kiện đủ”:

Định lí P:
- “Hai tam giác bằng nhau là điều kiện đủ để diện tích của chúng bằng nhau.” (Giả thiết là điều kiện đủ cho kết luận).
- “Diện tích của hai tam giác bằng nhau là điều kiện cần để hai tam giác đó bằng nhau.” (Kết luận là điều kiện cần cho giả thiết, hoặc giả thiết là điều kiện đủ cho kết luận).
Định lí Q:
- “a < b là điều kiện đủ để có a + c < b + c.” (Giả thiết là điều kiện đủ cho kết luận).
- “a + c < b + c là điều kiện cần để có a < b.” (Kết luận là điều kiện cần cho giả thiết).

c) Mệnh đề đảo của mỗi định lí đó có là định lí không?

Mệnh đề đảo của định lí P: “Nếu hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau”.
- Mệnh đề này là sai.
- Ví dụ phản chứng: Xét tam giác ABC vuông tại A có AB = 3, AC = 4, suy ra BC = 5. Diện tích là frac{1}{2} times 3 times 4 = 6. Xét tam giác MNP đều có cạnh 3sqrt{2}. Diện tích là frac{1}{2} times (3sqrt{2})^2 = frac{1}{2} times 18 = 9. Để tìm ví dụ đơn giản hơn: Hai tam giác có thể có cùng diện tích nhưng hình dạng khác nhau, ví dụ tam giác có đáy 6 và chiều cao 5 có diện tích là 15. Một tam giác khác có đáy 5 và chiều cao 6 cũng có diện tích là 15, nhưng hai tam giác này không bằng nhau.
- Vì mệnh đề đảo sai, nên nó không phải là định lí.
Mệnh đề đảo của định lí Q: “Nếu a + c < b + c thì a < b” (a, b, c ∈ ℝ).
- Mệnh đề này là đúng.
- Chứng minh:
  Ta có: a + c < b + c
  Trừ c ở cả hai vế (do phép cộng có tính chất kết hợp với phép trừ):
  a + c - c < b + c - c
  a < b
- Vì mệnh đề đảo đúng, nên nó là một định lí.

Bài 5 trang 15 Toán lớp 10 Tập 1

Sử dụng thuật ngữ “điều kiện cần và đủ”, các định lí được phát biểu như sau:

a) “Một phương trình bậc hai có hai nghiệm phân biệt là điều kiện cần và đủ để biệt thức của nó dương.”

b) “Một hình bình hành là hình thoi là điều kiện cần và đủ để hai đường chéo của nó vuông góc với nhau.”

Bài 6 trang 15 Toán lớp 10 Tập 1

a) Xét tính đúng sai của mỗi mệnh đề trên.

Mệnh đề P: “Giá trị tuyệt đối của mọi số thực đều lớn hơn hoặc bằng chính nó”.
- Phát biểu lại: ∀x ∈ ℝ, |x| ≥ x.
- Xét hai trường hợp:
  - Nếu x ≥ 0, thì |x| = x. Do đó |x| ≥ x đúng.
  - Nếu x < 0, thì |x| = -x. Vì x là số âm, -x là số dương, nên -x > x. Do đó |x| > x, suy ra |x| ≥ x đúng.
- Vậy mệnh đề P đúng.
Mệnh đề Q: “Có số tự nhiên sao cho bình phương của nó bằng 10”.
- Phát biểu lại: ∃n ∈ ℕ, n^2 = 10.
- Để n^2 = 10 với n là số tự nhiên, n phải là sqrt{10} hoặc -sqrt{10}.
- Tuy nhiên, sqrt{10} không phải là số tự nhiên (vì 3^2 = 9 và 4^2 = 16, không có số tự nhiên nào bình phương bằng 10). -sqrt{10} cũng không phải số tự nhiên.
- Vậy mệnh đề Q sai.
Mệnh đề R: “Có số thực x sao cho x^2 + 2x – 1 = 0”.
- Phát biểu lại: ∃x ∈ ℝ, x^2 + 2x – 1 = 0.
- Xét phương trình bậc hai x^2 + 2x – 1 = 0.
- Ta tính biệt thức Delta': Delta' = b'^2 - ac = 1^2 - (1)(-1) = 1 + 1 = 2.
- Vì Delta' = 2 > 0, phương trình có hai nghiệm phân biệt là các số thực.
- Cụ thể, nghiệm là x = dfrac{-b' pm sqrt{Delta'}}{a} = dfrac{-1 pm sqrt{2}}{1}.
- Vậy mệnh đề R đúng.

b) Sử dụng kí hiệu ∀, ∃ để viết lại các mệnh đề đã cho:

P: ∀x ∈ ℝ, |x| ≥ x
Q: ∃n ∈ ℕ, n^2 = 10
R: ∃x ∈ ℝ, x^2 + 2x – 1 = 0

Bài 7 trang 15 Toán lớp 10 Tập 1

a) Xét mệnh đề a) ∃x∈ℕ , x + 3 = 0:

Xét tính đúng sai:
- Ta có x + 3 = 0 ⇔ x = -3.
- Số -3 không thuộc tập hợp số tự nhiên ℕ.
- Do đó, không tồn tại số tự nhiên x thỏa mãn x + 3 = 0.
- Mệnh đề a) sai.
Viết mệnh đề phủ định:
- Mệnh đề ban đầu là ∃x ∈ ℕ, P(x) (với P(x) là x + 3 = 0).
- Mệnh đề phủ định là ∀x ∈ ℕ, ¬P(x).
- Mệnh đề phủ định là: ∀x ∈ ℕ, x + 3 ≠ 0.

b) Xét mệnh đề b) ∀x ∈ ℝ , x^2 + 1 ≥ 2x:

Xét tính đúng sai:
- Xét bất đẳng thức x^2 + 1 ≥ 2x.
- Chuyển vế: x^2 - 2x + 1 ≥ 0.
- Ta nhận ra đây là hằng đẳng thức: (x - 1)^2 ≥ 0.
- Bình phương của một số thực luôn không âm, tức là (x - 1)^2 ≥ 0 đúng với mọi số thực x.
- Mệnh đề b) đúng.
Viết mệnh đề phủ định:
- Mệnh đề ban đầu là ∀x ∈ ℝ, P(x) (với P(x) là x^2 + 1 ≥ 2x).
- Mệnh đề phủ định là ∃x ∈ ℝ, ¬P(x).
- Mệnh đề phủ định là: ∃x ∈ ℝ, x^2 + 1 < 2x.

c) Xét mệnh đề c) ∀a∈ℝ,a^2=a:

Xét tính đúng sai:
- Mệnh đề này khẳng định a^2 = a đúng với mọi số thực a.
- Ta xét trường hợp a = 2. Khi đó a^2 = 2^2 = 4. Ta có 4 ≠ 2.
- Do đó, mệnh đề a^2 = a không đúng với mọi số thực a.
- Mệnh đề c) sai.
Viết mệnh đề phủ định:
- Mệnh đề ban đầu là ∀a ∈ ℝ, P(a) (với P(a) là a^2 = a).
- Mệnh đề phủ định là ∃a ∈ ℝ, ¬P(a).
- Mệnh đề phủ định là: ∃a ∈ ℝ, a^2 ≠ a.

Đáp Án/Kết Quả

Bài 4: Xác định rõ giả thiết, kết luận; phát biểu đúng các định lí bằng thuật ngữ “điều kiện cần”, “điều kiện đủ”; nhận định đúng mệnh đề đảo của P sai và mệnh đề đảo của Q đúng.
Bài 5: Phát biểu đúng các định lí bằng thuật ngữ “điều kiện cần và đủ”.
Bài 6: P đúng, Q sai, R đúng. Viết đúng các mệnh đề bằng kí hiệu ∀, ∃.
Bài 7: Mệnh đề a) sai, phủ định là ∀x ∈ ℕ, x + 3 ≠ 0. Mệnh đề b) đúng, phủ định là ∃x ∈ ℝ, x^2 + 1 < 2x. Mệnh đề c) sai, phủ định là ∃a ∈ ℝ, a^2 ≠ a.

Mẹo kiểm tra

Khi xét định lí đảo, hãy nhớ tìm phản ví dụ hoặc chứng minh trực tiếp để xác định tính đúng sai.
Khi dùng kí hiệu ∀ và ∃, hãy chú ý đến tập hợp mà biến thuộc về (ví dụ: ∈ ℕ, ∈ ℝ) và cấu trúc của mệnh đề.
Luôn kiểm tra lại các phép toán và hằng đẳng thức khi biến đổi bất đẳng thức hoặc phương trình.

Lỗi hay gặp

Nhầm lẫn giữa “điều kiện cần” và “điều kiện đủ”. Nhớ rằng P là điều kiện đủ cho Q nếu P kéo theo Q (P ⇒ Q).
Việc áp dụng sai các tính chất của bất đẳng thức, ví dụ nhân hai vế với số âm mà không đổi chiều bất đẳng thức.
Quên mất tập xác định của biến khi sử dụng các lượng từ ∀, ∃.

Bài viết này cung cấp lời giải chi tiết cho các bài tập trang 15, Tập 1, Toán lớp 10 Chân trời sáng tạo, giúp học sinh nắm vững các khái niệm quan trọng về mệnh đề, định lí và cách sử dụng các kí hiệu logic.

Ngày chỉnh sửa nội dung mới nhất January 9, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.