Giải Toán 12 trang 24 Tập 1 Chân trời sáng tạo

by Thầy Đông · January 7, 2026

Rate this post

Lời Giải Chi Tiết Bài Tập Trang 24 Toán 12 Tập 1 Chân trời sáng tạo

Trang 24, Bài 3 “Đường tiệm cận của đồ thị hàm số” trong sách Toán 12 Tập 1 Chân trời sáng tạo bao gồm các bài tập quan trọng giúp học sinh củng cố kiến thức về tiệm cận đứng, tiệm cận ngang và tiệm cận xiên. Dưới đây là lời giải chi tiết cho từng bài tập, được trình bày rõ ràng và chuẩn xác về mặt toán học, sử dụng định dạng KaTeX để hiển thị công thức một cách tối ưu cho website WordPress.

Mục tiêu của trang này: Cung cấp lời giải chi tiết, dễ hiểu cho các bài tập về tiệm cận trong chương trình Toán 12, giúp học sinh nắm vững cách xác định các loại tiệm cận và áp dụng vào giải các dạng bài tập tương tự.

Đề Bài

Thực hành 3 trang 24 Toán 12 Tập 1:
Tìm tiệm cận xiên của đồ thị hàm số $y=\frac{2x^2-3x}{x+5}$ .

Thực hành 4 trang 24 Toán 12 Tập 1:
Nếu trong một ngày, một xưởng sản xuất được $x$ kilôgam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức: $C(x)=\frac{50x+2000}{x}$ . Tìm các đường tiệm cận của đồ thị hàm số $y = C(x)$ .

Bài 1 trang 24 Toán 12 Tập 1:
Tìm các tiệm cận đứng và tiệm cận ngang của đồ thị hàm số sau:
a) $y=\frac{4x-5}{2x-3}$ ;
b) $y=\frac{-2x+7}{4x-3}$ ;
c) $y=\frac{5x}{3x-7}$ .

Bài 2 trang 24 Toán 12 Tập 1:
Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số sau:
a) $y=\frac{x^2+2}{2x-4}$ ;
b) $y=\frac{2x^2-3x-6}{x+2}$ ;
c) $y=\frac{2x^2+9x+11}{2x+5}$ .

Bài 3 trang 24 Toán 12 Tập 1:
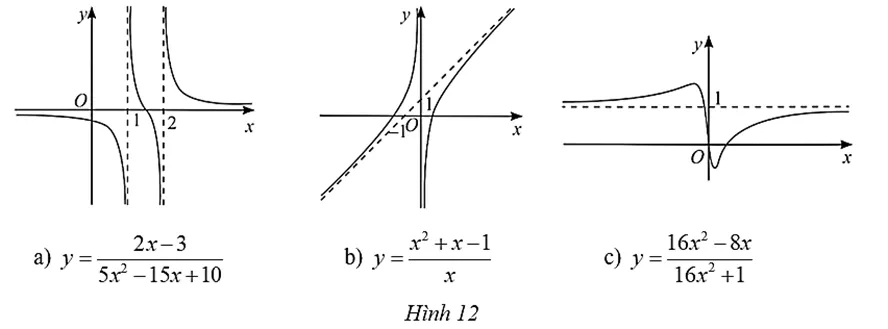
Tìm các tiệm cận của đồ thị hàm số sau (dựa vào đồ thị):
a)

Hình ảnh đồ thị hàm số ab)
Hình ảnh đồ thị hàm số bc)
Hình ảnh đồ thị hàm số c

Phân Tích Yêu Cầu

Các bài tập trên yêu cầu xác định các loại đường tiệm cận của đồ thị hàm số. Cụ thể:

Tiệm cận đứng: Là đường thẳng $x=a$ sao cho một trong các giới hạn $\lim{x \to a^+}$ hoặc $\lim{x \to a^-}$ bằng $+\infty$ hoặc $-\infty$ . Thông thường, ta tìm các giá trị $a$ làm cho mẫu số bằng 0 và tử số khác 0.
Tiệm cận ngang: Là đường thẳng $y=b$ sao cho $\lim{x \to +\infty} y$ hoặc $\lim{x \to -\infty} y$ bằng $b$ .
Tiệm cận xiên: Là đường thẳng $y=ax+b$ ( $a \ne 0$ ) sao cho $lim_{x \to \pm \infty} (y - (ax+b)) = 0$ . Điều này thường xảy ra khi bậc của tử số lớn hơn bậc của mẫu số đúng 1 bậc.

Việc phân tích kỹ yêu cầu và nắm vững định nghĩa của từng loại tiệm cận là bước đầu tiên để giải bài tập chính xác.

Kiến Thức/Nền Tảng Cần Dùng

Để giải quyết các bài toán về tiệm cận, học sinh cần nắm vững các kiến thức sau:

Giới hạn của hàm số:
- $\lim{x \to a^+} f(x)$ , $\lim{x \to a^-} f(x)$ , $lim_{x \to a} f(x)$ .
- $\lim{x \to +\infty} f(x)$ , $\lim{x \to -\infty} f(x)$ .
- Các quy tắc tính giới hạn, các dạng vô định ( $\frac{0}{0}$ , $\frac{\infty}{\infty}$ ).
Định nghĩa các loại tiệm cận:
- Tiệm cận đứng: Nếu $lim_{x \to a^{\pm}} f(x) = \pm \infty$ , thì $x=a$ là tiệm cận đứng. Đối với hàm phân thức $y=\frac{P(x)}{Q(x)}$ , tiệm cận đứng thường là các nghiệm của phương trình $Q(x)=0$ mà không là nghiệm của $P(x)=0$ .
- Tiệm cận ngang: Nếu lim_{x \to \pm \infty} f(x) = b, thì y=b là tiệm cận ngang.
 - Với hàm phân thức y=\frac{a_nx^n + \ldots}{b_mx^m + \ldots}:
 - Nếu $n < m[/katex], tiệm cận ngang là [katex]y=0[/katex].</li> <li>Nếu [katex]n = m$ , tiệm cận ngang là $y=\frac{a_n}{b_m}$ .
 - Nếu $n > m$ , không có tiệm cận ngang (có thể có tiệm cận xiên).
- Tiệm cận xiên: Đường thẳng $y=ax+b$ là tiệm cận xiên nếu $a = \lim{x \to \pm \infty} \frac{f(x)}{x}$ và $b = \lim{x \to \pm \infty} (f(x) - ax)$ . Đối với hàm phân thức, tiệm cận xiên tồn tại khi bậc tử số lớn hơn bậc mẫu số đúng 1. Ta có thể tìm $y=ax+b$ bằng cách chia đa thức.
Biến đổi đại số: Chia đa thức, phân tích nhân tử, rút gọn biểu thức.

Hướng Dẫn Giải Chi Tiết

Thực hành 3 trang 24

Đề bài: Tìm tiệm cận xiên của đồ thị hàm số $y=\frac{2x^2-3x}{x+5}$ .

Phân tích:
Bậc tử số ( $2$ ) lớn hơn bậc mẫu số ( $1$ ) đúng 1 bậc, nên có khả năng tồn tại tiệm cận xiên.

Các bước giải:

Tìm tập xác định:
Hàm số xác định khi $x+5 \ne 0$ , tức là $x \ne -5$ .
Tập xác định: $D = mathbb{R} setminus {-5}$ .
Thực hiện phép chia đa thức:
Ta chia tử thức $2x^2-3x$ cho mẫu thức $x+5$ .
$\begin{array}{c|cc cc} multicolumn{2}{r}{2x} & -13 cline{2-5} x+5 & 2x^2 & -3x & +0 multicolumn{2}{r}{2x^2} & +10x cline{2-3} multicolumn{2}{r}{0} & -13x & +0 multicolumn{2}{r}{} & -13x & -65 cline{3-4} multicolumn{2}{r}{} & 0 & +65 \end{array}$
Vậy ta có: $y=\frac{2x^2-3x}{x+5} = 2x-13 + \frac{65}{x+5}$ .
Tính giới hạn để xác định tiệm cận xiên:
Ta cần kiểm tra giới hạn của $y - (2x-13)$ khi $x \to \pm \infty$ .
$\lim{x \to +\infty} \left( y - (2x-13) \right) = \lim{x \to +\infty} \left( \left( 2x-13 + \frac{65}{x+5} \right) - (2x-13) \right) = \lim{x \to +\infty} \frac{65}{x+5}$
Khi $x \to +\infty$ , mẫu số $x+5 \to +\infty$ , do đó $\frac{65}{x+5} \to 0$ .
$\lim{x \to +\infty} \frac{65}{x+5} = 0$ .
Tương tự, khi $x \to -\infty$ :
$\lim{x \to -\infty} \left( y - (2x-13) \right) = \lim{x \to -\infty} \left( \left( 2x-13 + \frac{65}{x+5} \right) - (2x-13) \right) = \lim{x \to -\infty} \frac{65}{x+5}$
Khi $x \to -\infty$ , mẫu số $x+5 \to -\infty$ , do đó $\frac{65}{x+5} \to 0$ .
$\lim{x \to -\infty} \frac{65}{x+5} = 0$ .

Kết luận: Vì $lim_{x \to \pm \infty} (y - (2x-13)) = 0$ , đường thẳng $y = 2x-13$ là tiệm cận xiên của đồ thị hàm số.

Mẹo kiểm tra: Đảm bảo phép chia đa thức là chính xác. Giới hạn của phần dư sau khi chia phải tiến về 0 khi $x \to \pm \infty$ .
Lỗi hay gặp: Sai sót trong phép chia đa thức hoặc tính toán giới hạn.

Thực hành 4 trang 24

Đề bài: Tìm các đường tiệm cận của đồ thị hàm số $C(x)=\frac{50x+2000}{x}$ .

Phân tích: Đây là hàm phân thức có bậc tử số bằng bậc mẫu số, nên có khả năng có tiệm cận ngang và tiệm cận đứng.

Các bước giải:

Tìm tiệm cận đứng:
Mẫu số là $x$ . Đặt $x=0$ .
Ta xét giới hạn khi $x \to 0$ :
$\lim{x \to 0^+} C(x) = \lim{x \to 0^+} \frac{50x+2000}{x} = \frac{2000}{0^+} = +\infty$
$\lim{x \to 0^-} C(x) = \lim{x \to 0^-} \frac{50x+2000}{x} = \frac{2000}{0^-} = -\infty$
Do các giới hạn này bằng $\pm \infty$ , đường thẳng $x=0$ là tiệm cận đứng của đồ thị hàm số.
Tìm tiệm cận ngang:
Ta xét giới hạn khi $x \to \pm \infty$ .
Chia cả tử và mẫu cho $x$ :
$C(x) = \frac{50x+2000}{x} = \frac{50 + \frac{2000}{x}}{1}$
$\lim{x \to +\infty} C(x) = \lim{x \to +\infty} \left( 50 + \frac{2000}{x} \right) = 50 + 0 = 50$
$\lim{x \to -\infty} C(x) = \lim{x \to -\infty} \left( 50 + \frac{2000}{x} \right) = 50 + 0 = 50$
Do các giới hạn này bằng 50, đường thẳng $y=50$ là tiệm cận ngang của đồ thị hàm số.

Mẹo kiểm tra: Đối với hàm $y = \frac{ax+b}{cx+d}$ , tiệm cận đứng là $x=-\frac{d}{c}$ và tiệm cận ngang là $y=\frac{a}{c}$ .
Lỗi hay gặp: Nhầm lẫn giữa giới hạn tiến về 0 và giới hạn vô cùng.

Bài 1 trang 24

Đề bài: Tìm các tiệm cận đứng và tiệm cận ngang của đồ thị hàm số:
a) $y=\frac{4x-5}{2x-3}$ ;
b) $y=\frac{-2x+7}{4x-3}$ ;
c) $y=\frac{5x}{3x-7}$ .

Lời giải:

a) Hàm số: $y=\frac{4x-5}{2x-3}$

Tiệm cận đứng: Đặt mẫu số bằng 0: $2x-3=0 implies x=\frac{3}{2}$ .
Tử số tại $x=\frac{3}{2}$ là $4(\frac{3}{2})-5 = 6-5=1 \ne 0$ .
Do đó, $x=\frac{3}{2}$ là tiệm cận đứng.
Kiểm tra giới hạn:
$\lim{x \to (\frac{3}{2})^{+}} y = \lim{x \to (\frac{3}{2})^{+}} \frac{4x-5}{2x-3} = \frac{1}{0^+} = +\infty$
$\lim{x \to (\frac{3}{2})^{-}} y = \lim{x \to (\frac{3}{2})^{-}} \frac{4x-5}{2x-3} = \frac{1}{0^-} = -\infty$
Tiệm cận ngang: Bậc tử số ( $1$ ) bằng bậc mẫu số ( $1$ ).
$\lim{x \to \pm \infty} y = \lim{x \to \pm \infty} \frac{4x-5}{2x-3} = lim_{x \to \pm \infty} \frac{4-\frac{5}{x}}{2-\frac{3}{x}} = \frac{4}{2} = 2$ .
Do đó, $y=2$ là tiệm cận ngang.

b) Hàm số: $y=\frac{-2x+7}{4x-3}$

Tiệm cận đứng: Đặt mẫu số bằng 0: $4x-3=0 implies x=\frac{3}{4}$ .
Tử số tại $x=\frac{3}{4}$ là $-2(\frac{3}{4})+7 = -\frac{3}{2}+7 = \frac{11}{2} \ne 0$ .
Do đó, $x=\frac{3}{4}$ là tiệm cận đứng.
Kiểm tra giới hạn:
$\lim{x \to (\frac{3}{4})^{+}} y = \lim{x \to (\frac{3}{4})^{+}} \frac{-2x+7}{4x-3} = \frac{11/2}{0^+} = +\infty$
$\lim{x \to (\frac{3}{4})^{-}} y = \lim{x \to (\frac{3}{4})^{-}} \frac{-2x+7}{4x-3} = \frac{11/2}{0^-} = -\infty$
Tiệm cận ngang: Bậc tử số ( $1$ ) bằng bậc mẫu số ( $1$ ).
$\lim{x \to \pm \infty} y = \lim{x \to \pm \infty} \frac{-2x+7}{4x-3} = lim_{x \to \pm \infty} \frac{-2+\frac{7}{x}}{4-\frac{3}{x}} = \frac{-2}{4} = -\frac{1}{2}$ .
Do đó, $y=-\frac{1}{2}$ là tiệm cận ngang.

c) Hàm số: $y=\frac{5x}{3x-7}$

Tiệm cận đứng: Đặt mẫu số bằng 0: $3x-7=0 implies x=\frac{7}{3}$ .
Tử số tại $x=\frac{7}{3}$ là $5(\frac{7}{3})=\frac{35}{3} \ne 0$ .
Do đó, $x=\frac{7}{3}$ là tiệm cận đứng.
Kiểm tra giới hạn:
$\lim{x \to (\frac{7}{3})^{+}} y = \lim{x \to (\frac{7}{3})^{+}} \frac{5x}{3x-7} = \frac{35/3}{0^+} = +\infty$
$\lim{x \to (\frac{7}{3})^{-}} y = \lim{x \to (\frac{7}{3})^{-}} \frac{5x}{3x-7} = \frac{35/3}{0^-} = -\infty$
Tiệm cận ngang: Bậc tử số ( $1$ ) bằng bậc mẫu số ( $1$ ).
$\lim{x \to \pm \infty} y = \lim{x \to \pm \infty} \frac{5x}{3x-7} = lim_{x \to \pm \infty} \frac{5}{3-\frac{7}{x}} = \frac{5}{3}$ .
Do đó, $y=\frac{5}{3}$ là tiệm cận ngang.

Mẹo kiểm tra: Đối với hàm phân thức bậc nhất trên bậc nhất, chỉ cần so sánh hệ số của $x$ ở tử và mẫu để tìm tiệm cận ngang.
Lỗi hay gặp: Quên kiểm tra tử số khác 0 khi xác định tiệm cận đứng, hoặc tính sai giới hạn.

Bài 2 trang 24

Đề bài: Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số:
a) $y=\frac{x^2+2}{2x-4}$ ;
b) $y=\frac{2x^2-3x-6}{x+2}$ ;
c) $y=\frac{2x^2+9x+11}{2x+5}$ .

Lời giải:

a) Hàm số: $y=\frac{x^2+2}{2x-4}$

Tiệm cận đứng: Đặt mẫu số bằng 0: $2x-4=0 implies x=2$ .
Tử số tại $x=2$ là $2^2+2 = 4+2=6 \ne 0$ .
Do đó, $x=2$ là tiệm cận đứng.
Kiểm tra giới hạn: $\lim{x \to 2^+} y = +\infty$ , $\lim{x \to 2^-} y = -\infty$ .
Tiệm cận xiên: Bậc tử số ( $2$ ) lớn hơn bậc mẫu số ( $1$ ) là 1. Thực hiện phép chia đa thức:
$\frac{x^2+2}{2x-4} = \frac{1}{2}x + 1 + \frac{6}{2x-4}$
Ta có $a=\frac{1}{2}$ , $b=1$ .
$\lim{x \to \pm \infty} (y - (\frac{1}{2}x+1)) = \lim{x \to \pm \infty} \frac{6}{2x-4} = 0$ .
Vậy $y=\frac{1}{2}x+1$ là tiệm cận xiên.

b) Hàm số: $y=\frac{2x^2-3x-6}{x+2}$

Tiệm cận đứng: Đặt mẫu số bằng 0: $x+2=0 implies x=-2$ .
Tử số tại $x=-2$ là $2(-2)^2-3(-2)-6 = 2(4)+6-6 = 8 \ne 0$ .
Do đó, $x=-2$ là tiệm cận đứng.
Kiểm tra giới hạn: $\lim{x \to -2^+} y = +\infty$ , $\lim{x \to -2^-} y = -\infty$ .
Tiệm cận xiên: Bậc tử số ( $2$ ) lớn hơn bậc mẫu số ( $1$ ) là 1. Thực hiện phép chia đa thức:
$\frac{2x^2-3x-6}{x+2} = 2x-7 + \frac{8}{x+2}$
Ta có $a=2$ , $b=-7$ .
$\lim{x \to \pm \infty} (y - (2x-7)) = \lim{x \to \pm \infty} \frac{8}{x+2} = 0$ .
Vậy $y=2x-7$ là tiệm cận xiên.

c) Hàm số: $y=\frac{2x^2+9x+11}{2x+5}$

Tiệm cận đứng: Đặt mẫu số bằng 0: $2x+5=0 implies x=-\frac{5}{2}$ .
Tử số tại $x=-\frac{5}{2}$ là $2(-\frac{5}{2})^2+9(-\frac{5}{2})+11 = 2(\frac{25}{4})-\frac{45}{2}+11 = \frac{25}{2}-\frac{45}{2}+\frac{22}{2} = \frac{2}{2}=1 \ne 0$ .
Do đó, $x=-\frac{5}{2}$ là tiệm cận đứng.
Kiểm tra giới hạn: $\lim{x \to (-\frac{5}{2})^+} y = +\infty$ , $\lim{x \to (-\frac{5}{2})^-} y = -\infty$ .
Tiệm cận xiên: Bậc tử số ( $2$ ) lớn hơn bậc mẫu số ( $1$ ) là 1. Thực hiện phép chia đa thức:
$\frac{2x^2+9x+11}{2x+5} = x+2 + \frac{1}{2x+5}$
Ta có $a=1$ , $b=2$ .
$\lim{x \to \pm \infty} (y - (x+2)) = \lim{x \to \pm \infty} \frac{1}{2x+5} = 0$ .
Vậy $y=x+2$ là tiệm cận xiên.

Mẹo kiểm tra: Khi bậc tử là $n$ và bậc mẫu là $m$ , nếu $n=m+1$ , ta có thể dùng phép chia đa thức để tìm tiệm cận xiên.
Lỗi hay gặp: Sai sót trong phép chia đa thức, hoặc tính sai hệ số $a, b$ của tiệm cận xiên.

Bài 3 trang 24

Đề bài: Tìm các tiệm cận của đồ thị hàm số dựa vào đồ thị cho trước.

Lời giải:

a) Dựa vào đồ thị, ta quan sát các đường thẳng mà đồ thị tiến tới nhưng không bao giờ chạm tới.

Ta thấy đồ thị tiến rất gần đến trục tung $x=0$ và trục $x=1$ , đồng thời có xu hướng đi lên hoặc đi xuống vô hạn khi $x$ tiến gần các giá trị này. Do đó, $x=0$ và $x=1$ là hai tiệm cận đứng.
Đồ thị tiến rất gần đến trục hoành $y=0$ khi $x$ tiến ra vô cùng ( $x \to \pm \infty$ ). Do đó, $y=0$ là tiệm cận ngang.

b) Dựa vào đồ thị:

Đồ thị tiến rất gần đến trục tung $x=0$ và có xu hướng đi lên vô hạn khi $x$ tiến gần 0 từ phía bên phải, và đi xuống vô hạn khi $x$ tiến gần 0 từ phía bên trái. Do đó, $x=0$ là tiệm cận đứng.
Đồ thị có xu hướng đi theo một đường thẳng khi $x$ tiến ra vô cùng. Đường thẳng này có hệ số góc dương và đi qua điểm trên trục tung là $y=1$ . Bằng cách quan sát các điểm trên đồ thị, ta có thể ước lượng hoặc xác định chính xác đường tiệm cận xiên này là $y=x+1$ .

c) Dựa vào đồ thị:

Ta thấy đồ thị tiến rất gần đến đường thẳng $y=1$ khi $x$ tiến ra vô cùng ở cả hai phía. Do đó, $y=1$ là tiệm cận ngang.
Không có đường tiệm cận đứng nào được thể hiện rõ ràng trong đồ thị này (nếu có, đồ thị sẽ có xu hướng đi lên hoặc xuống vô hạn tại một giá trị $x$ cụ thể).

Mẹo kiểm tra: Khi đọc đồ thị, tìm các đường thẳng mà đồ thị "bám theo" hoặc tiến sát mà không cắt tại các điểm giới hạn hoặc khi $x \to \pm \infty$ .
Lỗi hay gặp: Nhầm lẫn giữa tiệm cận và các đường cong đi qua đồ thị, hoặc không xác định đúng giá trị của tiệm cận.

Đáp Án/Kết Quả

Thực hành 3: Tiệm cận xiên là $y=2x-13$ .
Thực hành 4: Tiệm cận đứng $x=0$ , tiệm cận ngang $y=50$ .
Bài 1:
- a) Tiệm cận đứng $x=\frac{3}{2}$ , tiệm cận ngang $y=2$ .
- b) Tiệm cận đứng $x=\frac{3}{4}$ , tiệm cận ngang $y=-\frac{1}{2}$ .
- c) Tiệm cận đứng $x=\frac{7}{3}$ , tiệm cận ngang $y=\frac{5}{3}$ .
Bài 2:
- a) Tiệm cận đứng $x=2$ , tiệm cận xiên $y=\frac{1}{2}x+1$ .
- b) Tiệm cận đứng $x=-2$ , tiệm cận xiên $y=2x-7$ .
- c) Tiệm cận đứng $x=-\frac{5}{2}$ , tiệm cận xiên $y=x+2$ .
Bài 3:
- a) Tiệm cận đứng $x=0, x=1$ , tiệm cận ngang $y=0$ .
- b) Tiệm cận đứng $x=0$ , tiệm cận xiên $y=x+1$ .
- c) Tiệm cận ngang $y=1$ .

Việc nắm vững cách tìm tiệm cận đứng, ngang và xiên là rất quan trọng để phân tích và hiểu rõ hơn về đồ thị hàm số. Trang 24, Bài 3 trong sách Toán 12 Chân trời sáng tạo cung cấp các bài tập thực hành cần thiết để củng cố kiến thức này, giúp học sinh tự tin giải quyết các dạng toán liên quan.

Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.