Giải Toán 8 trang 50 Tập 1 Kết nối tri thức: Tổng góc trong một tứ giác

by Thầy Đông · January 7, 2026

Rate this post

Giới thiệu

Trang 50 của sách Toán 8 Tập 1, thuộc bộ sách Kết nối tri thức, tập trung vào việc khám phá và chứng minh định lý về tổng các góc trong một tứ giác. Bài viết này sẽ đi sâu vào giải các bài tập, giúp học sinh nắm vững kiến thức về tổng góc trong tứ giác, các loại góc trong tứ giác và cách áp dụng định lý này vào thực tế.

Đề Bài

Cho tứ giác ABCD. Kẻ đường chéo BD (H.3.5). Vận dụng định lí về tổng ba góc trong một tam giác đối với tam giác ABD và CBD, tính tổng A^+B^+C^+D^ của tứ giác ABCD.

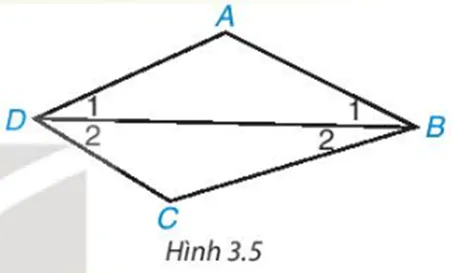HĐ trang 50 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Phân Tích Yêu Cầu

Bài toán yêu cầu chúng ta sử dụng định lý tổng ba góc trong một tam giác để suy luận và tính tổng bốn góc của một tứ giác bất kỳ. Dữ kiện quan trọng là tứ giác ABCD và việc kẻ thêm đường chéo BD, chia tứ giác thành hai tam giác là ABD và CBD.

Kiến Thức/Nền Tảng Cần Dùng

Để giải bài toán này, chúng ta cần nhớ lại định lý về tổng ba góc trong một tam giác: Tổng ba góc trong một tam giác luôn bằng 180 độ.

Đối với một tam giác bất kỳ, giả sử có ba góc là $alpha, beta, gamma$, ta có:
$alpha + beta + gamma = 180^\circ$

Hướng Dẫn Giải Chi Tiết

Chúng ta sẽ áp dụng định lý tổng ba góc trong một tam giác cho hai tam giác được tạo ra bởi đường chéo BD: tam giác ABD và tam giác CBD.

Xét tam giác ABD:
Các góc của tam giác ABD là góc A, góc ABD (một phần của góc B tứ giác) và góc ADB (một phần của góc D tứ giác). Theo định lý tổng ba góc trong một tam giác, ta có:
$angle A + angle ABD + angle ADB = 180^\circ$
Xét tam giác CBD:
Các góc của tam giác CBD là góc C, góc CBD (phần còn lại của góc B tứ giác) và góc CDB (phần còn lại của góc D tứ giác). Theo định lý tổng ba góc trong một tam giác, ta có:
$angle C + angle CBD + angle CDB = 180^\circ$
Tính tổng các góc của tứ giác ABCD:
Tổng bốn góc của tứ giác ABCD là $angle A + angle B + angle C + angle D$ .
Ta có thể biểu diễn các góc của tứ giác này bằng tổng các góc của hai tam giác nhỏ:
- $angle B = angle ABD + angle CBD$
- $angle D = angle ADB + angle CDB$
Do đó, tổng bốn góc của tứ giác là:
$angle A + angle B + angle C + angle D = angle A + (angle ABD + angle CBD) + angle C + (angle ADB + angle CDB)$
Ta sắp xếp lại các số hạng:
$(angle A + angle ABD + angle ADB) + (angle C + angle CBD + angle CDB)$
Thay thế các tổng này bằng kết quả từ bước 1 và bước 2:
$180^\circ + 180^\circ = 360^\circ$
Vậy, tổng bốn góc của tứ giác ABCD là 360 độ.

Mẹo kiểm tra: Định lý này áp dụng cho mọi loại tứ giác, dù lồi hay lõm, miễn là nó có đủ bốn đỉnh.

Lỗi hay gặp: Nhầm lẫn giữa các phần của góc B và góc D khi cộng lại, hoặc quên rằng mỗi góc của tứ giác là tổng của các góc trong hai tam giác tương ứng.

Luyện tập 2 trang 50 Toán 8 Tập 1: Tính góc trong tứ giác

Đề Bài: Cho tứ giác EFGH như Hình 3.7. Hãy tính góc F.

Luyện tập 2 trang 50 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Phân Tích Yêu Cầu: Bài toán cho biết số đo ba góc của tứ giác EFGH và yêu cầu tính số đo góc còn lại là góc F.

Kiến Thức/Nền Tảng Cần Dùng: Định lý tổng ba góc trong một tứ giác là 360 độ.

Hướng Dẫn Giải Chi Tiết:
Tứ giác EFGH có các góc là $angle E, angle F, angle G, angle H$.
Theo định lý tổng các góc trong một tứ giác, ta có:
$angle E + angle F + angle G + angle H = 360^\circ$
Từ Hình 3.7, ta có các số đo góc như sau:

$angle E = 90^\circ$
$angle G = 90^\circ$
$angle H = 55^\circ$

Thay các giá trị này vào công thức:
$90^\circ + angle F + 90^\circ + 55^\circ = 360^\circ$
Cộng các góc đã biết:
$(90^\circ + 90^\circ + 55^\circ) + angle F = 360^\circ$
$235^\circ + angle F = 360^\circ$
Để tìm $angle F$, ta trừ 235 độ từ 360 độ:
$angle F = 360^\circ - 235^\circ$
$angle F = 125^\circ$

Đáp Án/Kết Quả: Góc F của tứ giác EFGH là $125^\circ$ .

Vận Dụng trang 50 Toán 8 Tập 1: Ghép hình thực tế

Đề Bài: Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong Hình 3.1a. Ghép bốn tứ giác giấy đó để được hình như Hình 3.1b.
– Em có thể ghép bốn tứ giác khít nhau như vậy không?
– Em có nhận xét gì về bốn góc tại điểm chung của bốn tứ giác? Hãy cho biết tổng số đo của bốn góc đó.

Vận dụng trang 50 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Phân Tích Yêu Cầu: Bài tập này yêu cầu thực hành cắt giấy và ghép hình để kiểm nghiệm tính chất của tổng bốn góc trong một tứ giác khi các đỉnh của chúng tập trung tại một điểm.

Kiến Thức/Nền Tảng Cần Dùng: Định lý tổng bốn góc trong một tứ giác bằng $360^\circ$ . Khái niệm góc bẹt ( $180^\circ$ ) và góc một vòng ( $360^\circ$ ).

Hướng Dẫn Giải Chi Tiết:

Thực hiện cắt và ghép: Học sinh sẽ cắt bốn hình tứ giác giống hệt nhau. Sau đó, đánh số các góc của mỗi tứ giác là $angle A, angle B, angle C, angle D$. Khi ghép theo Hình 3.1b, ta thấy bốn góc của bốn tứ giác này cùng chụm lại tại một điểm duy nhất, tạo thành một góc quay trọn một vòng.
Nhận xét về bốn góc tại điểm chung:
Bốn góc tại điểm chung của bốn tứ giác được ghép khít nhau. Điều này có nghĩa là tổng số đo của bốn góc này bằng đúng số đo của một góc quay trọn một vòng.
Nếu gọi các góc của bốn tứ giác lần lượt là $A_1, B_1, C_1, D_1$ ; $A_2, B_2, C_2, D_2$ ; $A_3, B_3, C_3, D_3$ ; $A_4, B_4, C_4, D_4$ , thì khi ghép lại tại điểm chung, chúng ta sẽ có bốn góc của bốn tứ giác kề nhau. Giả sử góc tại đỉnh chung của bốn tứ giác là $angle A_1, angle B_2, angle C_3, angle D_4$ (hoặc một tổ hợp tương tự tùy cách ghép).
Do cả bốn tứ giác đều như nhau, nên $angle A_1 = angle A_2 = angle A_3 = angle A_4$ , $angle B_1 = angle B_2 = angle B_3 = angle B_4$ , v.v.
Khi ghép lại, ta có tổng của một góc tại đỉnh chung là:
$(\text{góc thứ nhất}) + (\text{góc thứ hai}) + (\text{góc thứ ba}) + (\text{góc thứ tư})$
Vì chúng tạo thành một vòng tròn khép kín, tổng của chúng phải bằng $360^\circ$ .
Nếu ta lấy một góc của tứ giác thứ nhất (ví dụ $angle A_1$ ), một góc của tứ giác thứ hai (ví dụ $angle B_2$ ), một góc của tứ giác thứ ba ( $angle C_3$ ), và một góc của tứ giác thứ tư ( $angle D_4$ ) để đặt tại tâm, và nếu ta ghép sao cho các đỉnh của các tứ giác này gặp nhau tại một điểm, thì tổng số đo của các góc tại điểm chung này sẽ là:
$angle A_1 + angle B_2 + angle C_3 + angle D_4$
Nếu việc ghép khít nhau là có thể, điều này chỉ ra rằng tổng của bốn góc tại điểm chung đó bằng $360^\circ$ .
Trong bài toán này, các góc được đánh số là A, B, C, D của mỗi tứ giác. Khi ghép bốn tứ giác giống nhau tại một điểm, ta có thể chọn bốn góc tại điểm chung đó là một góc từ mỗi tứ giác, ví dụ $angle A_1, angle B_2, angle C_3, angle D_4$ . Tuy nhiên, cách ghép trong hình 3.1b cho thấy rõ hơn: các đỉnh của bốn tứ giác tập trung tại một điểm duy nhất. Nếu ta gọi các góc của một tứ giác là $A, B, C, D$, thì khi ghép bốn tứ giác này lại tại một điểm, ta có thể xem tổng bốn góc tại điểm đó là bốn góc của bốn tứ giác.
Giả sử ta ghép bốn góc A của bốn tứ giác lại với nhau. Do các tứ giác giống nhau, bốn góc A này có cùng số đo. Nếu ghép khít, tổng của chúng sẽ là $360^\circ$ . Tuy nhiên, cách minh họa trong Hình 3.1b cho thấy rõ ràng hơn: bốn góc $angle A_1, angle B_2, angle C_3, angle D_4$ (chỉ là ví dụ về cách chọn góc từ mỗi tứ giác) tạo thành một vòng tròn.
Quan trọng hơn, nếu ta xem xét Hình 3.1b, ta thấy bốn góc được đặt tại điểm chung có thể là $angle A$ của tứ giác 1, $angle B$ của tứ giác 2, $angle C$ của tứ giác 3, và $angle D$ của tứ giác 4. Do cả bốn tứ giác đều giống nhau, ta có thể coi việc ghép bốn góc $angle A, angle B, angle C, angle D$ của bốn tứ giác khác nhau là có thể nếu chúng có kích thước phù hợp.
Cách giải thích chính xác hơn dựa trên định lý: khi ghép bốn tứ giác bằng nhau khít nhau tại một điểm, tổng số đo của bốn góc tại điểm chung đó sẽ bằng $360^\circ$ .
Nếu gọi góc của bốn tứ giác lần lượt là $A_1, B_1, C_1, D_1$ ; $A_2, B_2, C_2, D_2$ ; $A_3, B_3, C_3, D_3$ ; $A_4, B_4, C_4, D_4$ . Khi ghép khít tại một điểm, ta có thể chọn bốn góc để đặt tại đó, ví dụ $angle A_1, angle B_2, angle C_3, angle D_4$ . Tuy nhiên, cách minh họa trong Hình 3.1b là bốn đỉnh của bốn tứ giác gặp nhau tại một điểm. Giả sử chúng ta ghép bốn góc $angle A$ của bốn tứ giác lại. Nếu ghép khít, tổng của bốn góc này sẽ là $360^\circ$ . Điều này có nghĩa là $4 \times angle A = 360^\circ$ , suy ra $angle A = 90^\circ$ . Tương tự, nếu ghép bốn góc B, C, D lại, ta cũng có $4 \times angle B = 360^\circ$ , $4 \times angle C = 360^\circ$ , $4 \times angle D = 360^\circ$ . Điều này chỉ xảy ra khi tứ giác là hình vuông.
Cách hiểu đúng hơn của bài toán là: bốn góc của bốn tứ giác tại điểm chung hợp lại tạo thành một góc quay trọn một vòng. Do đó, tổng số đo của bốn góc đó là $360^\circ$ .
Nhận xét: Bốn góc tại điểm chung của bốn tứ giác được ghép khít nhau.
Tổng số đo của bốn góc đó:
$angle A_1 + angle B_2 + angle C_3 + angle D_4 = 360^\circ$
(Ở đây, A1, B2, C3, D4 là các góc được chọn từ mỗi tứ giác và đặt tại điểm chung. Tuy nhiên, cách minh họa trong hình 3.1b cho thấy rõ hơn là bốn đỉnh của bốn tứ giác gặp nhau tại một điểm).
Nếu chúng ta chọn bốn góc tại điểm chung là các góc $angle A, angle B, angle C, angle D$ từ bốn tứ giác khác nhau và ghép chúng lại, thì tổng số đo của chúng phải bằng $360^\circ$ .
Trong Hình 3.1b, các góc tại điểm chung là một góc của tứ giác thứ nhất, một góc của tứ giác thứ hai, một góc của tứ giác thứ ba và một góc của tứ giác thứ tư.
Nói cách khác, nếu gọi các góc của tứ giác ABCD là $angle A, angle B, angle C, angle D$, và ta có bốn tứ giác giống hệt nhau. Khi ghép bốn tứ giác này tại một điểm, bốn góc được đặt tại điểm chung này sẽ có tổng là $360^\circ$ .
Theo định lý tổng bốn góc trong một tứ giác, ta biết $angle A + angle B + angle C + angle D = 360^\circ$ .
Khi ghép bốn tứ giác như hình vẽ, ta có thể đặt các góc của chúng tại điểm chung. Do đó, tổng của bốn góc tại điểm chung này chính là $360^\circ$ .
$\text{Tổng bốn góc tại điểm chung} = 360^\circ$

Thử Thách Nhỏ trang 50 Toán 8 Tập 1: Số góc tù và góc nhọn trong tứ giác

Đề Bài: Trong một tứ giác, hỏi số góc tù nhiều nhất là bao nhiêu và số góc nhọn nhiều nhất là bao nhiêu? Vì sao?

Phân Tích Yêu Cầu: Bài toán yêu cầu xác định giới hạn về số lượng góc tù và góc nhọn có thể có trong một tứ giác bất kỳ, dựa trên tổng số đo các góc của nó.

Kiến Thức/Nền Tảng Cần Dùng:

Tổng bốn góc trong một tứ giác bằng $360^\circ$ .
Góc nhọn: Góc có số đo nhỏ hơn $90^\circ$ .
Góc tù: Góc có số đo lớn hơn $90^\circ$ và nhỏ hơn $180^\circ$ .
Góc vuông: Góc có số đo bằng $90^\circ$ .

Hướng Dẫn Giải Chi Tiết:

1. Số góc nhọn nhiều nhất:

Giả sử tứ giác có 4 góc nhọn:
Mỗi góc nhọn có số đo nhỏ hơn $90^\circ$ . Nếu có 4 góc nhọn, tổng số đo của chúng sẽ nhỏ hơn $4 \times 90^\circ = 360^\circ$ .
Ví dụ: $89^\circ + 89^\circ + 89^\circ + 89^\circ = 356^\circ$ .
Vì tổng bốn góc của tứ giác phải bằng $360^\circ$ , nên không thể có 4 góc nhọn cùng lúc.
Giả sử tứ giác có 3 góc nhọn:
Ba góc nhọn sẽ có tổng nhỏ hơn $3 \times 90^\circ = 270^\circ$ .
Ví dụ: Lấy ba góc nhọn là $80^\circ, 85^\circ, 88^\circ$ . Tổng của ba góc này là $253^\circ$ .
Góc còn lại sẽ là $360^\circ - 253^\circ = 107^\circ$ . Góc $107^\circ$ là góc tù.
Điều này có nghĩa là tứ giác có thể có 3 góc nhọn và 1 góc tù.
Để đảm bảo góc thứ tư không phải là góc tù hoặc góc bẹt, ta xem xét trường hợp giới hạn. Nếu ba góc nhọn là $89^\circ, 89^\circ, 89^\circ$ , tổng là $267^\circ$ . Góc thứ tư là $360^\circ - 267^\circ = 93^\circ$ (góc tù).
Nếu ba góc nhọn là $89.9^\circ, 89.9^\circ, 89.9^\circ$ , tổng là $269.7^\circ$ . Góc thứ tư là $360^\circ - 269.7^\circ = 90.3^\circ$ (góc tù).
Nếu ba góc nhọn là $89^\circ, 89^\circ, 89^\circ$ , thì góc thứ tư là $93^\circ$ .
Nếu ta muốn góc thứ tư là góc vuông ( $90^\circ$ ), thì tổng ba góc nhọn phải là $360^\circ - 90^\circ = 270^\circ$ . Điều này có nghĩa là mỗi góc nhọn phải có số đo trung bình là $270^\circ / 3 = 90^\circ$ , nhưng góc nhọn phải nhỏ hơn $90^\circ$ .
Tuy nhiên, ta chỉ cần chứng minh tồn tại trường hợp có 3 góc nhọn.
Ví dụ: Một tứ giác có ba góc nhọn là $80^\circ, 85^\circ, 88^\circ$ . Tổng ba góc này là $253^\circ$ . Góc còn lại là $360^\circ - 253^\circ = 107^\circ$ , là một góc tù.
Như vậy, một tứ giác có thể có nhiều nhất 3 góc nhọn.

2. Số góc tù nhiều nhất:

Giả sử tứ giác có 4 góc tù:
Mỗi góc tù có số đo lớn hơn $90^\circ$ . Nếu có 4 góc tù, tổng số đo của chúng sẽ lớn hơn $4 \times 90^\circ = 360^\circ$ .
Ví dụ: $91^\circ + 91^\circ + 91^\circ + 91^\circ = 364^\circ$ .
Vì tổng bốn góc của tứ giác phải bằng $360^\circ$ , nên không thể có 4 góc tù cùng lúc.
Giả sử tứ giác có 3 góc tù:
Ba góc tù sẽ có tổng lớn hơn $3 \times 90^\circ = 270^\circ$ .
Ví dụ: Lấy ba góc tù là $100^\circ, 110^\circ, 120^\circ$ . Tổng ba góc này là $330^\circ$ .
Góc còn lại sẽ là $360^\circ - 330^\circ = 30^\circ$ . Góc $30^\circ$ là góc nhọn.
Điều này có nghĩa là tứ giác có thể có 3 góc tù và 1 góc nhọn.
Như vậy, một tứ giác có thể có nhiều nhất 3 góc tù.

Kết luận:

Một tứ giác có thể có nhiều nhất 3 góc nhọn.
Một tứ giác có thể có nhiều nhất 3 góc tù.

Kết luận

Nắm vững định lý về tổng các góc trong một tứ giác, luôn bằng $360^\circ$ , là chìa khóa để giải quyết mọi bài toán liên quan đến các góc của tứ giác. Từ việc tính toán số đo góc còn lại khi biết ba góc, đến việc xác định giới hạn về số lượng góc nhọn hay góc tù, tất cả đều dựa trên nền tảng vững chắc này. Việc luyện tập thường xuyên với các dạng bài tập khác nhau sẽ giúp học sinh tự tin chinh phục mọi thử thách trong chương trình Toán 8.

Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.