Giải Toán 8 trang 122 Tập 2 Kết nối Tri Thức: Hướng Dẫn Chi Tiết

by Thầy Đông · January 8, 2026

Rate this post

Tóm tắt bài viết: Bài viết này cung cấp lời giải chi tiết cho các bài tập Toán 8 trang 122, Tập 2, thuộc bộ sách Kết nối Tri Thức. Nội dung bao gồm các bài tập về nhận dạng và tính thể tích, diện tích xung quanh của hình chóp tam giác đều và hình chóp tứ giác đều. Chúng tôi sẽ phân tích kỹ lưỡng từng bước giải, cung cấp kiến thức nền tảng cần thiết và mẹo để học sinh có thể tự tin chinh phục dạng bài này. Đặc biệt, bài viết tuân thủ chuẩn mực trình bày công thức toán học bằng KaTeX, đảm bảo tính chính xác và dễ đọc.

Đề Bài

Bài 10.12 trang 122 Toán 8 Tập 2: Trong các miếng bìa ở Hình 10.32, miếng bìa nào khi gấp và dán lại thì được một hình chóp tam giác đều, miếng nào thì được một hình chóp tứ giác đều.

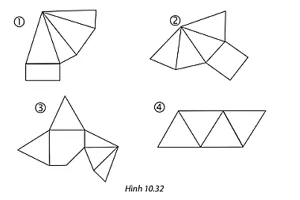Hình 10.32 – Các miếng bìa để gấp hình chóp

Bài 10.13 trang 122 Toán 8 Tập 2: Tính thể tích hình chóp tam giác đều A.BCD có độ dài cạnh đáy bằng 10 cm, chiều cao bằng 12 cm (H.10.33), biết $\sqrt{75} \approx 8,66$ .

Bài 10.14 trang 122 Toán 8 Tập 2: Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao 21 m, độ dài cạnh đáy là 34 m.
a) Tính thể tích hình chóp.
b) Tính tổng diện tích các tấm kính để phủ kín bốn mặt bên hình chóp này, biết rằng người ta đo được độ dài cạnh bên của hình chóp là 31,92 m.

Mô hình kim tự tháp Louvre

Phân Tích Yêu Cầu

Các bài tập trang 122, Tập 2, Toán 8 Kết nối Tri Thức tập trung vào việc ứng dụng kiến thức về hình chóp đều vào thực tế và tính toán các đại lượng cơ bản như thể tích, diện tích xung quanh.

Bài 10.12: Yêu cầu nhận dạng các mẫu gấp để tạo thành hình chóp tam giác đều hoặc hình chóp tứ giác đều. Điều này đòi hỏi học sinh phải hiểu cấu trúc của các loại hình chóp này, cụ thể là hình dạng của đáy và các mặt bên.
Bài 10.13: Đòi hỏi tính toán thể tích của một hình chóp tam giác đều khi biết độ dài cạnh đáy và chiều cao. Bài toán cung cấp sẵn giá trị xấp xỉ của căn bậc hai, giúp việc tính toán diện tích đáy trở nên đơn giản hơn.
Bài 10.14: Là một bài toán thực tế phức tạp hơn, yêu cầu tính cả thể tích và diện tích xung quanh của hình chóp tứ giác đều. Dữ kiện bài toán cho bao gồm chiều cao, cạnh đáy và cạnh bên. Việc tính diện tích xung quanh sẽ cần xác định trung đoạn của hình chóp.

Kiến Thức/Nền Tảng Cần Dùng

Để giải quyết các bài tập này, chúng ta cần nắm vững các khái niệm và công thức sau:

1. Hình Chóp Đều

Hình chóp tam giác đều: Là hình chóp có đáy là tam giác đều và các mặt bên là các tam giác cân bằng nhau. Chân đường cao hạ từ đỉnh xuống đáy trùng với tâm của tam giác đều (trọng tâm, trực tâm, tâm đường tròn ngoại tiếp và nội tiếp).
Hình chóp tứ giác đều: Là hình chóp có đáy là hình vuông và các mặt bên là các tam giác cân bằng nhau. Chân đường cao hạ từ đỉnh xuống đáy trùng với tâm của hình vuông (giao điểm hai đường chéo).

2. Các Công Thức Tính Toán Cơ Bản

Diện tích đáy (S):
- Tam giác đều cạnh a: $S = \dfrac{a^2 \sqrt{3}}{4}$
- Hình vuông cạnh a: $S = a^2$
Thể tích hình chóp (V): Công thức chung cho mọi loại hình chóp là:
$V = \dfrac{1}{3} \times S_{\text{đáy}} \times h$
Trong đó:
- $S_{\text{đáy}}$ là diện tích mặt đáy.
- $h$ là chiều cao của hình chóp (khoảng cách từ đỉnh đến mặt đáy).
Diện tích xung quanh hình chóp đều (Sxq): Công thức chung là:
$S_{\text{xq}} = p \times d$
Trong đó:
- $p$ là nửa chu vi đáy.
- $d$ là trung đoạn của hình chóp (chiều cao của một mặt bên kẻ từ đỉnh của hình chóp).

3. Định Lí Pythagore

Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông. Nếu tam giác vuông có các cạnh là a, b và cạnh huyền là c, thì:
$a^2 + b^2 = c^2$

Định lý này rất quan trọng để tính toán các độ dài chưa biết trong các tam giác vuông được tạo thành từ chiều cao, trung đoạn và các phần của đáy hoặc cạnh bên.

Hướng Dẫn Giải Chi Tiết

Bài 10.12: Nhận dạng hình chóp

Yêu cầu: Xác định miếng bìa nào tạo thành hình chóp tam giác đều và hình chóp tứ giác đều.

Phân tích:
Để gấp thành một hình chóp, các mặt bên khi được gấp lại sẽ gặp nhau tại đỉnh. Đáy của hình chóp sẽ là mặt không phải là tam giác cân hay hình thang cân (trừ trường hợp đáy là tam giác đều).

Hình chóp tam giác đều: Có đáy là tam giác đều. Các mặt bên là 3 tam giác cân bằng nhau.
Hình chóp tứ giác đều: Có đáy là hình vuông. Các mặt bên là 4 tam giác cân bằng nhau.

Xem xét từng miếng bìa trong Hình 10.32:

Miếng bìa 1: Có một mặt là hình thang cân và hai mặt là tam giác cân. Nếu đáy là hình thang cân, thì các mặt bên phải là tam giác. Miếng này có vẻ phức tạp và không tạo thành hình chóp đều tiêu chuẩn.
Miếng bìa 2: Có một mặt là hình vuông và bốn mặt là các tam giác cân. Khi gấp các tam giác cân này lên, chúng sẽ gặp nhau tại đỉnh tạo thành hình chóp có đáy là hình vuông. Đây là hình chóp tứ giác đều.
Miếng bìa 3: Có đáy là một hình bình hành không phải hình vuông hoặc hình thoi, và các mặt bên là tam giác. Khó tạo thành hình chóp đều.
Miếng bìa 4: Có một mặt là tam giác đều và ba mặt là các tam giác cân. Khi gấp ba tam giác cân lên, chúng sẽ gặp nhau tại đỉnh, còn tam giác đều sẽ là đáy. Đây là hình chóp tam giác đều.

Đáp án/Kết quả:

Miếng bìa 4 khi gấp và dán lại thì được một hình chóp tam giác đều.
Miếng bìa 2 khi gấp và dán lại thì được một hình chóp tứ giác đều.
Miếng bìa 1 và miếng bìa 3 không tạo thành hình chóp đều theo định nghĩa thông thường.

Mẹo kiểm tra: Hãy tưởng tượng hoặc vẽ lại cách gấp các miếng bìa. Đối với hình chóp đều, đáy phải là một đa giác đều (tam giác đều, hình vuông, ngũ giác đều,…) và các mặt bên phải là các tam giác cân bằng nhau.

Lỗi hay gặp: Nhầm lẫn giữa hình chóp đều và hình chóp không đều, hoặc chỉ đơn giản là không nhận ra hình dạng của đáy từ các miếng bìa được cho sẵn.

Bài 10.13: Tính thể tích hình chóp tam giác đều

Đề bài: Tính thể tích hình chóp tam giác đều A.BCD có độ dài cạnh đáy bằng 10 cm, chiều cao bằng 12 cm (H.10.33), biết $\sqrt{75} \approx 8,66$ .

Phân tích:
Để tính thể tích hình chóp, ta cần biết diện tích đáy và chiều cao. Bài toán đã cho chiều cao $h = 12$ cm. Đáy là tam giác đều BCD có cạnh $a = 10$ cm. Ta cần tính diện tích tam giác đều BCD.

Kiến thức cần dùng:

Công thức tính thể tích hình chóp: $V = \dfrac{1}{3} \times S_{\text{đáy}} \times h$
Công thức tính diện tích tam giác đều cạnh $a$ : $S = \dfrac{a^2 \sqrt{3}}{4}$
Định lý Pythagore (để tính chiều cao của tam giác đều hoặc dùng khi dữ kiện cho khác).

Hướng dẫn giải chi tiết:

Tính diện tích đáy S_{BCD}:
Tam giác BCD là tam giác đều có cạnh $a = 10$ cm.
Để tính diện tích tam giác đều, ta có thể dùng công thức $S = \dfrac{a^2 \sqrt{3}}{4}$ .
Thay $a = 10$ vào công thức:
$S_{\text{BCD}} = \dfrac{10^2 \sqrt{3}}{4} = \dfrac{100 \sqrt{3}}{4} = 25 \sqrt{3}$ (cm²).
Mẹo kiểm tra: Bạn có thể tính chiều cao $ID$ của tam giác đều (với I là trung điểm BC) bằng định lý Pythagore trong tam giác vuông BID: $ID^2 = BD^2 - BI^2 = 10^2 - 5^2 = 100 - 25 = 75$ . Do đó, $ID = \sqrt{75}$ .
Diện tích tam giác đáy BCD là: $S{\text{BCD}} = \dfrac{1}{2} \times \text{đáy} \times \text{chiều cao} = \dfrac{1}{2} \times BC \times ID = \dfrac{1}{2} \times 10 \times \sqrt{75}$ .
Sử dụng giá trị xấp xỉ $\sqrt{75} \approx 8,66$ cho sẵn trong đề bài:
$S{\text{BCD}} \approx \dfrac{1}{2} \times 10 \times 8,66 = 5 \times 8,66 = 43,3$ (cm²).
Tính thể tích hình chóp V_{A.BCD}:
Ta có chiều cao của hình chóp $h = 12$ cm và diện tích đáy $S{\text{BCD}} \approx 43,3$ cm².
Áp dụng công thức thể tích:
$V = \dfrac{1}{3} \times S{\text{đáy}} \times h$
$V \approx \dfrac{1}{3} \times 43,3 \times 12$
$V \approx 43,3 \times 4$
$V \approx 173,2$ (cm³).

Đáp án/Kết quả:
Thể tích hình chóp tam giác đều A.BCD là xấp xỉ 173,2 cm³.

Mẹo kiểm tra: Đơn vị đo thể tích phải là đơn vị lập phương (ví dụ: cm³). Hãy kiểm tra lại các phép tính nhân chia, đặc biệt là khi làm tròn số.

Lỗi hay gặp: Nhầm lẫn giữa chiều cao của tam giác đáy và chiều cao của hình chóp. Sử dụng sai công thức tính diện tích tam giác đều hoặc công thức thể tích hình chóp. Sai sót trong tính toán căn bậc hai hoặc phép nhân/chia.

Bài 10.14: Tính thể tích và diện tích xung quanh hình chóp tứ giác đều (Mô hình Kim tự tháp Louvre)

Đề bài: Mô hình có dạng hình chóp tứ giác đều, chiều cao 21 m, độ dài cạnh đáy là 34 m.
a) Tính thể tích hình chóp.
b) Tính tổng diện tích các tấm kính để phủ kín bốn mặt bên hình chóp này, biết rằng người ta đo được độ dài cạnh bên của hình chóp là 31,92 m.

Phân tích:
Đây là bài toán áp dụng công thức tính thể tích và diện tích xung quanh cho hình chóp tứ giác đều. Ta cần xác định rõ các đại lượng đã cho và các đại lượng cần tìm.

Đáy là hình vuông cạnh $a = 34$ m.
Chiều cao của hình chóp $h = 21$ m.
Cạnh bên của hình chóp $l = 31,92$ m.

Kiến thức cần dùng:

Công thức tính thể tích hình chóp: $V = \dfrac{1}{3} \times S_{\text{đáy}} \times h$
Công thức tính diện tích xung quanh hình chóp tứ giác đều: $S_{\text{xq}} = p \times d$
Định lí Pythagore để tìm trung đoạn $d$ .

Hướng dẫn giải chi tiết:

a) Tính thể tích hình chóp:

Tính diện tích đáy (S_{đáy}):
Đáy là hình vuông có cạnh $a = 34$ m.
$S_{\text{đáy}} = a^2 = 34^2$
$34^2 = 1156$ (m²).
Tính thể tích hình chóp (V):
Ta có chiều cao $h = 21$ m và diện tích đáy $S{\text{đáy}} = 1156$ m².
Áp dụng công thức thể tích:
$V = \dfrac{1}{3} \times S{\text{đáy}} \times h$
$V = \dfrac{1}{3} \times 1156 \times 21$
$V = 1156 \times \dfrac{21}{3}$
$V = 1156 \times 7$
$V = 8092$ (m³).

b) Tính tổng diện tích các tấm kính (Diện tích xung quanh):

Xác định trung đoạn (d):
Gọi đỉnh của hình chóp là S. Đáy là hình vuông EFGH. Chiều cao là SI, với I là tâm hình vuông.
Trung đoạn là đường cao của một mặt bên, ví dụ SK, với K là trung điểm của một cạnh đáy (ví dụ GH).
Tam giác SKH vuông tại K.
Ta có:
- SH là cạnh bên của hình chóp, $SH = 31,92$ m.
- KH là nửa cạnh đáy, $KH = \dfrac{GH}{2} = \dfrac{34}{2} = 17$ m.
- SK là trung đoạn ( $d$ ).
Áp dụng định lý Pythagore cho tam giác SKH vuông tại K:
$SK^2 + KH^2 = SH^2$
$d^2 + 17^2 = (31,92)^2$
$d^2 + 289 = 1018,8864$
$d^2 = 1018,8864 - 289$
$d^2 = 729,8864$
$d = \sqrt{729,8864} \approx 27,016$ m.
(Đề bài có thể làm tròn $\sqrt{729,8864} \approx 27,02$ m để tính toán).
Tính chu vi đáy và nửa chu vi đáy (p):
Chu vi đáy hình vuông là $C = 4 \times a = 4 \times 34 = 136$ m.
Nửa chu vi đáy là $p = \dfrac{C}{2} = \dfrac{136}{2} = 68$ m.
Tính diện tích xung quanh (Sxq):
Áp dụng công thức:
$S{\text{xq}} = p \times d$
$S{\text{xq}} \approx 68 \times 27,016$
$S{\text{xq}} \approx 1837,088$ (m²).
Nếu dùng giá trị $d \approx 27,02$ m từ đề bài:
$S{\text{xq}} \approx 68 \times 27,02 = 1837,36$ (m²).

Đáp án/Kết quả:
a) Thể tích hình chóp là 8092 m³.
b) Tổng diện tích các tấm kính để phủ kín bốn mặt bên hình chóp này là khoảng 1837,36 m².

Mẹo kiểm tra:

Thể tích: Đơn vị phải là m³. Kiểm tra lại phép tính $1156 \times 7$ .
Diện tích xung quanh: Đơn vị phải là m².
- Trung đoạn ( $d$ ) phải lớn hơn chiều cao ( $h$ ) và nhỏ hơn cạnh bên ( $l$ ). Ở đây $21 < 27,02 < 31,92[/katex], điều này hợp lý.</li> <li>Kiểm tra lại phép tính [katex]17^2$ , katex^2[/katex] và phép trừ, căn bậc hai.
- Kiểm tra phép nhân $68 \times 27,02$ .

Lỗi hay gặp:

Nhầm lẫn giữa cạnh đáy, cạnh bên, chiều cao và trung đoạn.
Sử dụng sai định lý Pythagore hoặc áp dụng sai cho tam giác nào.
Tính sai diện tích đáy hình vuông hoặc nửa chu vi đáy.
Nhầm lẫn công thức thể tích và diện tích xung quanh.
Sai sót trong quá trình làm tròn số, dẫn đến kết quả cuối cùng khác biệt.

Conclusion

Các bài tập Toán 8 trang 122, Tập 2, Kết nối Tri Thức đã trang bị cho học sinh kiến thức thực tiễn quý báu về hình chóp đều. Thông qua việc giải các bài toán về nhận dạng hình dạng, tính thể tích và diện tích xung quanh, các em được rèn luyện kỹ năng áp dụng công thức toán học vào các tình huống cụ thể, từ đó nâng cao khả năng tư duy logic và giải quyết vấn đề. Việc nắm vững các công thức về thể tích $V = \dfrac{1}{3} S{\text{đáy}} h$ và diện tích xung quanh $S{\text{xq}} = p \times d$ , cùng với định lý Pythagore, là chìa khóa để chinh phục thành công các dạng bài tập này, góp phần xây dựng nền tảng vững chắc cho các cấp học tiếp theo.

Ngày chỉnh sửa nội dung mới nhất January 8, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.