Giải Toán 9 Trang 22 Tập 2 Chân Trời Sáng Tạo: Hướng Dẫn Chi Tiết Và Bài Giải Chuẩn Xác

by Thầy Đông · January 7, 2026

Rate this post

Để giúp các em học sinh lớp 9 nắm vững kiến thức và tự tin chinh phục các bài tập trong sách giáo khoa, bài viết này cung cấp lời giải chi tiết và phân tích sâu sắc cho giải toán 9 tập 2 trang 22 thuộc chương trình Chân Trời Sáng Tạo. Chúng tôi tập trung vào việc trình bày các bước giải logic, dễ hiểu, đồng thời đảm bảo tính chính xác học thuật và định dạng chuẩn cho nội dung toán học.

Đề Bài

Nội dung bài tập trang 22, tập 2, sách Toán lớp 9 Chân Trời Sáng Tạo bao gồm các câu hỏi trắc nghiệm và tự luận về hàm số bậc hai, phương trình bậc hai và các ứng dụng liên quan.

Phân Tích Yêu Cầu

Các bài tập tại trang 22, tập 2, chủ yếu tập trung vào việc củng cố và vận dụng các kiến thức đã học về hàm số bậc hai $y=ax^2$ và phương trình bậc hai một ẩn. Yêu cầu chung là học sinh cần:

Xác định đúng nghiệm của phương trình bậc hai.
Vận dụng định lý Vi-et để tính tổng và tích các nghiệm.
Xác định hệ số $a$ của hàm số bậc hai khi biết một điểm thuộc đồ thị.
Vẽ đồ thị hàm số bậc hai.
Tìm tọa độ các điểm thuộc đồ thị thỏa mãn điều kiện cho trước.
Nhận dạng phương trình bậc hai một ẩn.

Để giải quyết tốt các bài tập này, học sinh cần nắm vững lý thuyết về hàm số bậc hai, công thức nghiệm phương trình bậc hai, định lý Vi-et và kỹ năng vẽ đồ thị hàm số.

Kiến Thức/Nền Tảng Cần Dùng

Trong quá trình giải các bài tập tại trang 22, tập 2, các kiến thức sau đây là nền tảng cốt lõi:

Hàm số bậc hai:
- Dạng tổng quát: $y = ax^2$ với $a \ne 0$ .
- Đồ thị của hàm số $y = ax^2$ là một parabol có đỉnh tại gốc tọa độ $O(0;0)$.
- Nếu $a > 0$, parabol có bề lõm quay lên trên.
- Nếu $a < 0$, parabol có bề lõm quay xuống dưới.
- Nếu đồ thị đi qua điểm $M(x_0; y_0)$ , thì tọa độ của điểm $M$ phải thỏa mãn phương trình: $y_0 = ax_0^2$ .
Phương trình bậc hai một ẩn:
- Dạng tổng quát: $ax^2 + bx + c = 0$ với $a \ne 0$ .
- Biệt thức Delta: \Delta = b^2 - 4ac.
 - Nếu $\Delta > 0$ , phương trình có hai nghiệm phân biệt: $x_{1,2} = \frac{-b \pm \sqrt{\Delta}}{2a}$ .
 - Nếu $\Delta = 0$ , phương trình có nghiệm kép: $x_1 = x_2 = \frac{-b}{2a}$ .
 - Nếu \Delta < 0[/katex], phương trình vô nghiệm.</li> </ul> </li> <li>Biệt thức thu gọn Delta phẩy: Nếu [katex]b = 2b', ta có \Delta' = (b')^2 - ac.
 - Nếu $\Delta' > 0$ , phương trình có hai nghiệm phân biệt: $x_{1,2} = \frac{-b' \pm \sqrt{\Delta'}}{a}$ .
 - Nếu $\Delta' = 0$ , phương trình có nghiệm kép: $x_1 = x_2 = \frac{-b'}{a}$ .
 - Nếu \Delta' < 0[/katex], phương trình vô nghiệm.</li> </ul> </li> </ul> </li> <li> Định lý Vi-et: Nếu phương trình bậc hai [katex]ax^2 + bx + c = 0 có hai nghiệm x_1, x_2, thì:
 - Tổng hai nghiệm: $S = x_1 + x_2 = -\frac{b}{a}$ .
 - Tích hai nghiệm: $P = x_1 \cdot x_2 = \frac{c}{a}$ .
 - Khi đó, ta có thể biểu diễn các biểu thức chứa $x_1, x_2$ qua $S$ và $P$. Ví dụ: $x_1^2 + x_2^2 = (x_1 + x_2)^2 - 2x_1x_2 = S^2 - 2P$ .
 - Phương trình bậc nhất: Dạng $ax + b = 0$ . Nếu $a \ne 0$ , có nghiệm duy nhất $x = -b/a$ . Nếu $a=0, b \ne 0$ , vô nghiệm. Nếu $a=0, b=0$ , vô số nghiệm.

Hướng Dẫn Giải Chi Tiết

Chúng ta sẽ đi qua từng bài tập cụ thể từ trang 22, tập 2.

Bài 3 trang 22 Toán 9 Tập 2

Đề bài: Cho hàm số $y = 2x^2$ . Khi $y = 2$ thì
A. $x = 1$ .
B. $x = 2$ hoặc $x = -2$ .
C. $x = 1$ hoặc $x = -1$ .
D. $x = 2$ .

Phân tích: Bài toán yêu cầu tìm giá trị của $x$ khi biết giá trị của $y$ cho trước và biểu thức của hàm số bậc hai.

Các bước giải:

Thay giá trị $y = 2$ vào phương trình hàm số $y = 2x^2$ .
Giải phương trình bậc hai thu được để tìm $x$.

Giải:
Thay $y = 2$ vào phương trình $y = 2x^2$ , ta có:
$2 = 2x^2$
Chia cả hai vế cho 2:
$x^2 = 1$
Lấy căn bậc hai hai vế:
$x = pmsqrt{1}$
$x = 1 quad \text{hoặc} quad x = -1$

Mẹo kiểm tra:
Thay các giá trị $x=1$ và $x=-1$ vào hàm số $y=2x^2$ :

Với $x=1$ , ta có $y = 2(1)^2 = 2(1) = 2$ .
Với $x=-1$ , ta có $y = 2(-1)^2 = 2(1) = 2$ .
Cả hai giá trị đều cho $y=2$ , do đó kết quả là đúng.

Lỗi hay gặp:

Quên trường hợp nghiệm âm khi lấy căn bậc hai ( $x^2=1$ chỉ ghi $x=1$ ).
Nhầm lẫn giữa $x^2 = 1$ và $x = 1$ .

Đáp án đúng: C. $x = 1$ hoặc $x = -1$ .

Bài 4 trang 22 Toán 9 Tập 2

Đề bài: Đồ thị hàm số $y = ax^2$ ( $a \ne 0$ ) đi qua điểm $(2; -2)$ . Giá trị của $a$ bằng
A. 2.
B. $-2$ .
C. $\frac{1}{2}$ .
D. $-\frac{1}{2}$ .

Phân tích: Bài toán cho biết đồ thị hàm số bậc hai đi qua một điểm cụ thể và yêu cầu tìm hệ số $a$.

Các bước giải:

Vì điểm $(2; -2)$ thuộc đồ thị hàm số $y = ax^2$ , nên tọa độ của điểm này thỏa mãn phương trình của hàm số.
Thay $x=2$ và $y=-2$ vào phương trình $y = ax^2$ để tìm $a$.

Giải:
Thay tọa độ điểm $(2; -2)$ vào phương trình $y = ax^2$ , ta có:
$-2 = a \cdot (2)^2$
$-2 = a \cdot 4$
$a = \frac{-2}{4}$
$a = -\frac{1}{2}$

Mẹo kiểm tra:
Thay giá trị $a = -\frac{1}{2}$ vào phương trình hàm số, ta được $y = -\frac{1}{2}x^2$ .
Kiểm tra xem điểm $(2; -2)$ có thuộc đồ thị này không:
Khi $x=2$ , $y = -\frac{1}{2}(2)^2 = -\frac{1}{2}(4) = -2$ .
Giá trị $y=-2$ khớp với tọa độ của điểm, vậy $a = -\frac{1}{2}$ là đúng.

Lỗi hay gặp:

Nhầm lẫn vai trò của $x$ và $y$ khi thay vào phương trình.
Sai sót trong phép tính hoặc quy đồng mẫu số.

Đáp án đúng: D. $-\frac{1}{2}$ .

Bài 5 trang 22 Toán 9 Tập 2

Đề bài: Nghiệm của phương trình $x^2 - 14x + 13 = 0$ là
A. $x_1 = -1; x_2 = 13$ .
B. $x_1 = -1; x_2 = -13$ .
C. $x_1 = 1; x_2 = -13$ .
D. $x_1 = 1; x_2 = 13$ .

Phân tích: Bài toán yêu cầu tìm nghiệm của một phương trình bậc hai.

Các bước giải:

Xác định các hệ số $a, b, c$ của phương trình bậc hai $ax^2 + bx + c = 0$ .
Tính biệt thức Delta ( $\Delta$ ) hoặc Delta phẩy ( $\Delta'$ ) để xác định số nghiệm.
Áp dụng công thức nghiệm để tìm $x_1$ và $x_2$ .

Giải:
Phương trình đã cho là $x^2 - 14x + 13 = 0$ .
Ta có các hệ số: $a = 1$ , $b = -14$ , $c = 13$ .

Cách 1: Sử dụng Delta
Tính biệt thức Delta:
$\Delta = b^2 - 4ac = (-14)^2 - 4(1)(13) = 196 - 52 = 144$
Vì $\Delta = 144 > 0$ , phương trình có hai nghiệm phân biệt.
$\sqrt{\Delta} = \sqrt{144} = 12$
Nghiệm thứ nhất:
$x_1 = \frac{-b + \sqrt{\Delta}}{2a} = \frac{-(-14) + 12}{2(1)} = \frac{14 + 12}{2} = \frac{26}{2} = 13$
Nghiệm thứ hai:
$x_2 = \frac{-b - \sqrt{\Delta}}{2a} = \frac{-(-14) - 12}{2(1)} = \frac{14 - 12}{2} = \frac{2}{2} = 1$

Cách 2: Sử dụng Delta phẩy (vì $b$ chẵn)
$b = -14$ , nên $b' = \frac{b}{2} = -7$ .
Tính biệt thức Delta phẩy:
$\Delta' = (b')^2 - ac = (-7)^2 - (1)(13) = 49 - 13 = 36$
Vì $\Delta' = 36 > 0$ , phương trình có hai nghiệm phân biệt.
$\sqrt{\Delta'} = \sqrt{36} = 6$
Nghiệm thứ nhất:
$x_1 = \frac{-b' + \sqrt{\Delta'}}{a} = \frac{-(-7) + 6}{1} = \frac{7 + 6}{1} = 13$
Nghiệm thứ hai:
$x_2 = \frac{-b' - \sqrt{\Delta'}}{a} = \frac{-(-7) - 6}{1} = \frac{7 - 6}{1} = 1$

Mẹo kiểm tra:

Sử dụng định lý Vi-et:
- Tổng nghiệm: $x_1 + x_2 = 13 + 1 = 14$ . Theo công thức Vi-et: $-\frac{b}{a} = -\frac{-14}{1} = 14$ . Khớp.
- Tích nghiệm: $x_1 \cdot x_2 = 13 \cdot 1 = 13$ . Theo công thức Vi-et: $\frac{c}{a} = \frac{13}{1} = 13$ . Khớp.
Thay nghiệm tìm được vào phương trình gốc để kiểm tra.

Lỗi hay gặp:

Tính toán sai Delta hoặc Delta phẩy.
Sai dấu khi áp dụng công thức nghiệm.
Nhầm lẫn giữa nghiệm $x_1$ và $x_2$ .

Đáp án đúng: D. $x_1 = 1; x_2 = 13$ .

Bài 6 trang 22 Toán 9 Tập 2

Đề bài: Phương trình nào dưới đây không là phương trình bậc hai một ẩn?
A. $x^2 - 7x + 7 = 0$ .
B. $3x^2 + 5x - 2 = 0$ .
C. $2x^2 - 2365 = 0$ .
D. $-7x + 25 = 0$ .

Phân tích: Bài toán yêu cầu xác định phương trình không thuộc dạng bậc hai một ẩn.

Định nghĩa: Phương trình bậc hai một ẩn có dạng tổng quát là $ax^2 + bx + c = 0$ , trong đó $a \ne 0$ .

Phân tích từng phương án:
A. $x^2 - 7x + 7 = 0$ : Đây là phương trình bậc hai vì có $a = 1 \ne 0$ .
B. $3x^2 + 5x - 2 = 0$ : Đây là phương trình bậc hai vì có $a = 3 \ne 0$ .
C. $2x^2 - 2365 = 0$ : Đây là phương trình bậc hai vì có $a = 2 \ne 0$ . (Ở đây $b=0$ ).
D. $-7x + 25 = 0$ : Đây là phương trình bậc nhất vì hệ số của $x^2$ (tức là $a$) bằng 0. Ta có thể viết lại là $0x^2 - 7x + 25 = 0$ .

Giải thích:
Phương trình bậc hai một ẩn yêu cầu hệ số $a$ (hệ số của $x^2$ ) phải khác 0.
Trong phương án D, phương trình $-7x + 25 = 0$ có thể được xem là $0x^2 - 7x + 25 = 0$ . Ở đây, hệ số $a=0$ , do đó nó không phải là phương trình bậc hai một ẩn mà là phương trình bậc nhất một ẩn.

Lỗi hay gặp:

Không nhớ rõ điều kiện $a \ne 0$ cho phương trình bậc hai.
Bị nhầm lẫn giữa bậc của phương trình.

Đáp án đúng: D. $-7x + 25 = 0$ .

Bài 7 trang 22 Toán 9 Tập 2

Đề bài: Gọi $S$ và $P$ lần lượt là tổng và tích của hai nghiệm của phương trình $x^2 + 5x - 10 = 0$ . Khi đó giá trị của $S$ và $P$ là
A. $S = 5; P = 10$ .
B. $S = -5; P = 10$ .
C. $S = -5; P = -10$ .
D. $S = 5; P = -10$ .

Phân tích: Bài toán yêu cầu áp dụng trực tiếp định lý Vi-et để tìm tổng và tích hai nghiệm của phương trình bậc hai.

Các bước giải:

Xác định các hệ số $a, b, c$ của phương trình.
Áp dụng công thức định lý Vi-et: $S = x_1 + x_2 = -\frac{b}{a}$ và $P = x_1 \cdot x_2 = \frac{c}{a}$ .

Giải:
Phương trình đã cho là $x^2 + 5x - 10 = 0$ .
Ta có các hệ số: $a = 1$ , $b = 5$ , $c = -10$ .

Áp dụng định lý Vi-et:
Tổng hai nghiệm $S$:
$S = x_1 + x_2 = -\frac{b}{a} = -\frac{5}{1} = -5$
Tích hai nghiệm $P$:
$P = x_1 \cdot x_2 = \frac{c}{a} = \frac{-10}{1} = -10$

Mẹo kiểm tra:
Trước hết, cần kiểm tra xem phương trình có nghiệm hay không bằng cách tính Delta.
$\Delta = b^2 - 4ac = (5)^2 - 4(1)(-10) = 25 + 40 = 65$
Vì $\Delta = 65 > 0$ , phương trình có hai nghiệm phân biệt, nên định lý Vi-et có thể áp dụng.
Kết quả $S = -5$ và $P = -10$ là chính xác.

Lỗi hay gặp:

Nhầm lẫn dấu khi áp dụng công thức $S = -\frac{b}{a}$ .
Nhầm lẫn giữa $b$ và $c$ khi áp dụng công thức $P = \frac{c}{a}$ .

Đáp án đúng: C. $S = -5; P = -10$ .

Bài 8 trang 22 Toán 9 Tập 2

Đề bài: Cho phương trình $x^2 + 7x - 15 = 0$ . Gọi $x_1, x_2$ là hai nghiệm của phương trình. Khi đó giá trị của biểu thức $x_1^2 + x_2^2 - x_1x_2$ là
A. 79.
B. 94.
C. -94.
D. -79.

Phân tích: Bài toán yêu cầu tính giá trị của một biểu thức đối xứng qua hai nghiệm $x_1, x_2$ của phương trình bậc hai, bằng cách sử dụng định lý Vi-et.

Các bước giải:

Xác định hệ số $a, b, c$ của phương trình.
Tính Delta để kiểm tra phương trình có nghiệm hay không.
Áp dụng định lý Vi-et để tìm $S = x_1 + x_2$ và $P = x_1 \cdot x_2$ .
Biến đổi biểu thức cần tính theo $S$ và $P$.
Thay giá trị $S$ và $P$ vào biểu thức đã biến đổi để tính kết quả.

Giải:
Phương trình đã cho là $x^2 + 7x - 15 = 0$ .
Ta có các hệ số: $a = 1$ , $b = 7$ , $c = -15$ .

Kiểm tra Delta:
$\Delta = b^2 - 4ac = (7)^2 - 4(1)(-15) = 49 + 60 = 109$
Vì $\Delta = 109 > 0$ , phương trình có hai nghiệm phân biệt $x_1, x_2$ .

Áp dụng định lý Vi-et:
$S = x_1 + x_2 = -\frac{b}{a} = -\frac{7}{1} = -7$
$P = x_1 \cdot x_2 = \frac{c}{a} = \frac{-15}{1} = -15$

Biểu thức cần tính là $x_1^2 + x_2^2 - x_1x_2$ .
Ta biến đổi biểu thức này như sau:
$x_1^2 + x_2^2 - x_1x_2 = (x_1^2 + 2x_1x_2 + x_2^2) - 2x_1x_2 - x_1x_2$
$= (x_1 + x_2)^2 - 3x_1x_2$
Thay $S$ và $P$ vào biểu thức này:
$= S^2 - 3P$
$= (-7)^2 - 3(-15)$
$= 49 - (-45)$
$= 49 + 45$
$= 94$

Mẹo kiểm tra:

Kiểm tra lại các phép tính Delta, S, P.
Kiểm tra lại bước biến đổi biểu thức: $(x_1 + x_2)^2 = x_1^2 + 2x_1x_2 + x_2^2$ . Do đó $x_1^2 + x_2^2 = (x_1 + x_2)^2 - 2x_1x_2$ .
Thay vào biểu thức ban đầu: $(x_1 + x_2)^2 - 2x_1x_2 - x_1x_2 = (x_1 + x_2)^2 - 3x_1x_2$ . Bước biến đổi là đúng.
Kiểm tra lại phép thế $S$ và $P$ vào.

Lỗi hay gặp:

Sai sót trong việc tính Delta, $S$ hoặc $P$.
Sai sót trong biến đổi biểu thức (ví dụ: nhầm $S^2-2P$ thành $S^2-3P$ hoặc ngược lại).
Sai phép tính số học cuối cùng.

Đáp án đúng: B. 94.

Bài 9 trang 22 Toán 9 Tập 2

Đề bài: Cho hai hàm số: $y = \frac{3}{2}x^2$ và $y = -x^2$ . Vẽ đồ thị của hai hàm số đã cho trên cùng mặt phẳng tọa độ Oxy.

Phân tích: Bài toán yêu cầu vẽ đồ thị của hai hàm số bậc hai có dạng $y=ax^2$ trên cùng một hệ trục tọa độ.

Các bước giải:

Lập bảng giá trị: Chọn các giá trị của $x$ (thường là các số nguyên như $0, \pm 1, \pm 2$ ) và tính giá trị $y$ tương ứng cho từng hàm số.
Xác định tọa độ các điểm: Từ bảng giá trị, ta có các cặp tọa độ $(x, y)$ thuộc đồ thị.
Vẽ đồ thị:
- Vẽ trục tọa độ Oxy.
- Xác định các điểm đã tính ở bước 2 lên mặt phẳng tọa độ.
- Nối các điểm này bằng đường cong mượt mà để tạo thành hình parabol. Lưu ý:
 - Parabol $y = \frac{3}{2}x^2$ có $a = \frac{3}{2} > 0$ , bề lõm quay lên trên, đỉnh tại $O(0;0)$.
 - Parabol $y = -x^2$ có $a = -1 < 0[/katex], bề lõm quay xuống dưới, đỉnh tại $O(0;0)$.</li> </ul> </li> </ul> </li> </ol> Giải: 1. Lập bảng giá trị: <ul> <li> Với hàm số [katex]y = \frac{3}{2}x^2$ :
 | $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
 | :------------ | :--- | :------ | :-- | :------ | :-- |
 | $y = \frac{3}{2}x^2$ | $6$ | $\frac{3}{2}$ | $0$ | $\frac{3}{2}$ | $6$ |
 - Với hàm số $y = -x^2$ :
 | $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
 | :----- | :--- | :--- | :-- | :-- | :-- |
 | $y = -x^2$ | $-4$ | $-1$ | $0$ | $-1$ | $-4$ |
 2. Xác định tọa độ các điểm:
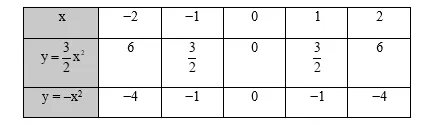
 - Hàm số $y = \frac{3}{2}x^2$ : Các điểm có thể là $(-2; 6), (-1; \frac{3}{2}), (0; 0), (1; \frac{3}{2}), (2; 6)$ .
 - Hàm số $y = -x^2$ : Các điểm có thể là $(-2; -4), (-1; -1), (0; 0), (1; -1), (2; -4)$ .
 3. Vẽ đồ thị:
 - Vẽ trục tọa độ Oxy.
 - Đánh dấu các điểm đã tìm được cho mỗi hàm số.
 - Nối các điểm $(-2; 6), (-1; \frac{3}{2}), (0; 0), (1; \frac{3}{2}), (2; 6)$ bằng một đường parabol có bề lõm hướng lên trên, đỉnh tại $O(0;0)$.
 - Nối các điểm $(-2; -4), (-1; -1), (0; 0), (1; -1), (2; -4)$ bằng một đường parabol có bề lõm hướng xuống dưới, đỉnh tại $O(0;0)$.
 Lưu ý: Do yêu cầu về định dạng và không thể vẽ hình trực tiếp, phần "hình ảnh" trong bài gốc sẽ được giữ nguyên định dạng gốc.
 Hình ảnh minh họa (theo bài gốc):
 Bài 9 trang 22 Toán 9 Tập 2 Chân trời sáng tạo | Giải Toán 9Đồ thị hai hàm số $y = \frac{3}{2}x^2$ và $y = -x^2$ trên cùng mặt phẳng tọa độ Oxy.
 Bài 9 trang 22 Toán 9 Tập 2 Chân trời sáng tạo | Giải Toán 9Chi tiết đồ thị hai hàm số $y = \frac{3}{2}x^2$ và $y = -x^2$ .
 Mẹo kiểm tra:
 - Đảm bảo các điểm đã đánh dấu nằm chính xác trên đồ thị.
 - Đồ thị phải có đỉnh tại gốc tọa độ.
 - Đồ thị $y = \frac{3}{2}x^2$ phải nằm phía trên trục hoành (trừ gốc tọa độ), đồ thị $y = -x^2$ phải nằm phía dưới trục hoành (trừ gốc tọa độ).
 Lỗi hay gặp:
 - Lập bảng giá trị sai.
 - Nhầm lẫn giữa bề lõm hướng lên hay hướng xuống.
 - Các điểm đánh dấu không chính xác.
 - Nối các điểm không tạo thành đường cong parabol mượt mà.
 Bài 10 trang 22 Toán 9 Tập 2
 Đề bài: Cho hàm số $y = ax^2$ ( $a \ne 0$ ).
 a) Tìm $a$ để đồ thị hàm số đi qua điểm $M(2; 2)$.
 b) Vẽ đồ thị $(P)$ của hàm số với $a$ vừa tìm được.
 c) Tìm các điểm thuộc đồ thị $(P)$ có tung độ $y = 8$ .
 Phân tích: Bài toán yêu cầu tìm hệ số $a$, vẽ đồ thị hàm số bậc hai, và tìm điểm thuộc đồ thị dựa trên điều kiện tung độ.
 Giải:
 a) Tìm $a$ để đồ thị hàm số đi qua điểm $M(2; 2)$.
 Thay tọa độ điểm $M(2; 2)$ vào phương trình $y = ax^2$ :
 $2 = a \cdot (2)^2$
 $2 = a \cdot 4$
 $a = \frac{2}{4} = \frac{1}{2}$
 Vậy, hệ số cần tìm là $a = \frac{1}{2}$ .
 b) Vẽ đồ thị $(P)$ của hàm số với $a$ vừa tìm được.
 Hàm số cần vẽ đồ thị là $y = \frac{1}{2}x^2$ .
 - Lập bảng giá trị:
 | $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
 | :------------ | :--- | :------ | :-- | :------ | :-- |
 | $y = \frac{1}{2}x^2$ | $2$ | $\frac{1}{2}$ | $0$ | $\frac{1}{2}$ | $2$ |
 - Các điểm thuộc đồ thị: $(-2; 2), (-1; \frac{1}{2}), (0; 0), (1; \frac{1}{2}), (2; 2)$ .
 - Vẽ đồ thị: Vẽ một parabol có đỉnh tại $O(0;0)$, bề lõm quay lên trên (vì $a = \frac{1}{2} > 0$ ), đi qua các điểm đã cho.
 Hình ảnh minh họa (theo bài gốc):
 Đồ thị hàm số $y = \frac{1}{2}x^2$ .
 Bài 10 trang 22 Toán 9 Tập 2 Chân trời sáng tạo | Giải Toán 9Chi tiết đồ thị hàm số $y = \frac{1}{2}x^2$ .
 c) Tìm các điểm thuộc đồ thị $(P)$ có tung độ $y = 8$ .
 Ta có phương trình hàm số là $y = \frac{1}{2}x^2$ .
 Thay $y = 8$ vào phương trình:
 $8 = \frac{1}{2}x^2$
 Nhân cả hai vế với 2:
 $16 = x^2$
 Lấy căn bậc hai hai vế:
 $x = pmsqrt{16}$
 $x = 4 quad \text{hoặc} quad x = -4$
 Vậy, có hai điểm thuộc đồ thị có tung độ $y=8$ là $(-4; 8)$ và $(4; 8)$.
 Mẹo kiểm tra:
 - Đối với phần c), thay các giá trị x = 4 và x = -4 vào hàm số y = \frac{1}{2}x^2 để kiểm tra xem $y$ có bằng 8 không.
 - Với $x=4$ : $y = \frac{1}{2}(4)^2 = \frac{1}{2}(16) = 8$ .
 - Với $x=-4$ : $y = \frac{1}{2}(-4)^2 = \frac{1}{2}(16) = 8$ .
 Kết quả kiểm tra cho thấy sự chính xác.
 Lỗi hay gặp:
 - Quên trường hợp nghiệm âm khi giải $x^2 = 16$ .
 - Nhầm lẫn giữa hệ số $a$ và tọa độ điểm khi tìm $a$.
 Bài 11 trang 22 Toán 9 Tập 2
 Đề bài: Giải các phương trình:
 a) $x^2 - 12x = 0$ ;
 b) $13x^2 + 25x - 38 = 0$ ;
 c) $3x^2 - \frac{4}{3}x + 4 = 0$ ;
 d) $x(x + 3) = 27 - (11 - 3x)$ .
 Phân tích: Bài toán yêu cầu giải nhiều dạng phương trình khác nhau: phương trình bậc hai khuyết hệ số, phương trình bậc hai đầy đủ, phương trình bậc hai với hệ số phân số, và phương trình đưa về bậc hai.
 Giải chi tiết từng câu:
 a) $x^2 - 12x = 0$
 Đây là phương trình bậc hai khuyết hệ số $c$.
 Ta có thể đặt nhân tử chung $x$:
 $x(x - 12) = 0$
 Áp dụng quy tắc "một tích bằng không khi một trong các thừa số bằng không":
 $x = 0 quad \text{hoặc} quad x - 12 = 0$
 $x = 0 quad \text{hoặc} quad x = 12$
 Nghiệm của phương trình là $x = 0$ và $x = 12$ .
 b) $13x^2 + 25x - 38 = 0$
 Đây là phương trình bậc hai đầy đủ. Ta thử kiểm tra các trường hợp đặc biệt của nghiệm.
 Xét tổng các hệ số: $a + b + c = 13 + 25 + (-38) = 38 - 38 = 0$ .
 Khi $a + b + c = 0$ , phương trình có hai nghiệm là $x_1 = 1$ và $x_2 = \frac{c}{a}$ .
 Vậy, ta có:
 $x_1 = 1$
 $x_2 = \frac{-38}{13}$
 Nghiệm của phương trình là $x = 1$ và $x = -\frac{38}{13}$ .
 c) $3x^2 - \frac{4}{3}x + 4 = 0$
 Đây là phương trình bậc hai với hệ số phân số.
 Ta có các hệ số: $a = 3$ , $b = -\frac{4}{3}$ , $c = 4$ .
 Để dễ tính toán, ta có thể quy đồng mẫu số hoặc làm việc trực tiếp với phân số. Ta sẽ dùng Delta phẩy vì $b$ có thể chia cho 2 một cách hợp lý ( $b' = -\frac{4}{3} div 2 = -\frac{2}{3}$ ).
 Tính Delta phẩy:
 $\Delta' = (b')^2 - ac = \left(-\frac{2}{3}\right)^2 - 3(4)$
 $\Delta' = \frac{4}{9} - 12$
 Để trừ hai số, ta quy đồng mẫu số: $12 = \frac{12 \times 9}{9} = \frac{108}{9}$ .
 $\Delta' = \frac{4}{9} - \frac{108}{9} = \frac{4 - 108}{9} = \frac{-104}{9}$
 Vì $\Delta' = \frac{-104}{9} < 0[/katex], phương trình vô nghiệm. Lưu ý kiểm tra lại đề bài, có thể có lỗi đánh máy ở câu c. Nếu đề bài là [katex]3x^2 - \frac{4}{3}x - 4 = 0$ , thì Delta' sẽ dương. Tuy nhiên, theo đề bài gốc, Delta' âm.
 Phương trình vô nghiệm.
 d) $x(x + 3) = 27 - (11 - 3x)$
 Đây là phương trình có thể đưa về dạng bậc hai.
 Mở rộng hai vế của phương trình:
 $x^2 + 3x = 27 - 11 + 3x$
 $x^2 + 3x = 16 + 3x$
 Chuyển tất cả các hạng tử về một vế:
 $x^2 + 3x - 3x - 16 = 0$
 $x^2 - 16 = 0$
 Đây là phương trình bậc hai khuyết hệ số $b$ và $c$ (hoặc có thể xem là dạng $x^2 - m^2 = 0$ ).
 $x^2 = 16$
 Lấy căn bậc hai hai vế:
 $x = pmsqrt{16}$
 $x = 4 quad \text{hoặc} quad x = -4$
 Nghiệm của phương trình là $x = 4$ và $x = -4$ .
 Mẹo kiểm tra:
 - Đối với câu a) và d), thay nghiệm tìm được vào phương trình gốc.
 - Đối với câu b), kiểm tra $a+b+c=0$ có đúng không và tính $c/a$ .
 - Đối với câu c), kiểm tra lại phép tính Delta'.
 Lỗi hay gặp:
 - Giải phương trình khuyết hệ số sai (quên nghiệm $x=0$ ).
 - Nhầm lẫn công thức nghiệm hoặc Delta/Delta'.
 - Sai sót trong phép tính phân số.
 - Không rút gọn hoặc nhân sai khi đưa phương trình về dạng chuẩn.
 Conclusion
 Bài tập trang 22, tập 2, sách Toán lớp 9 Chân Trời Sáng Tạo đã cung cấp một hệ thống các bài toán củng cố kiến thức về hàm số bậc hai và phương trình bậc hai. Bằng việc phân tích kỹ lưỡng từng bài tập, chúng ta đã làm rõ phương pháp giải, các kiến thức cần áp dụng và những lỗi sai thường gặp. Hy vọng rằng những lời giải chi tiết này sẽ giúp các em học sinh không chỉ giải được bài toán giải toán 9 tập 2 trang 22 mà còn nắm vững bản chất, từ đó tự tin giải quyết các bài toán tương tự trong tương lai.
 Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông
 Thầy Đông
 Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
 Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.