Giải Toán 9 trang 95 Tập 2 Chân trời Sáng tạo: Vận dụng và Khám phá Hình cầu

by Thầy Đông · January 7, 2026

Rate this post

Trong chương trình Toán lớp 9, việc hiểu rõ các khái niệm hình học và biết cách áp dụng chúng vào thực tế là vô cùng quan trọng. Bài viết này tập trung vào giải toán 9 trang 95 tập 2 thuộc bộ sách Chân trời Sáng tạo, giúp học sinh củng cố kiến thức về hình cầu thông qua các bài tập Vận dụng và Khám phá. Chúng ta sẽ đi sâu vào từng bước giải, phân tích yêu cầu và liên hệ với các kiến thức nền tảng, đảm bảo sự chính xác và dễ hiểu cho mọi đối tượng.

Đề Bài

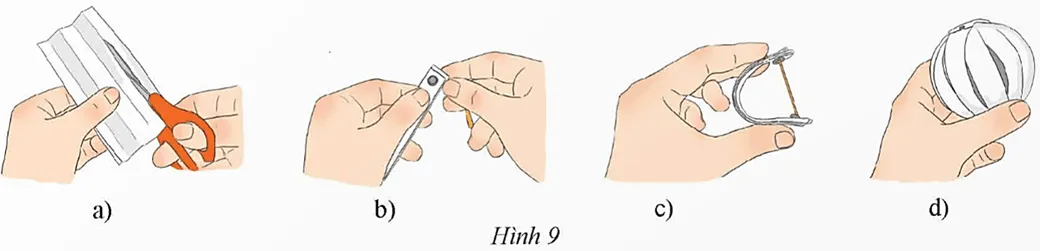
Vận dụng 1 trang 95 Toán 9 Tập 2: Gấp chiếc đèn trang trí dạng hình cầu (mặt cầu) theo hướng dẫn sau:
− Cắt các mảnh giấy hình chữ nhật có chiều dài 20 cm, chiều rộng 1 cm (Hình 9a).
− Đục lỗ rồi dùng nút gắn vào nhau (Hình 9b).
− Cố định hai lỗ bằng que tre có độ dài bằng 2xπ (khoảng 0,6x) với x là khoảng cách giữa hai cái lỗ (Hình 9c).
− Tách các mảnh giấy ra và trải đều, hình được tạo thành có dạng hình cầu (Hình 9d).

Vận dụng 1 trang 95 Toán 9 Tập 2 Chân trời sáng tạo | Giải Toán 9

Khám phá 3 trang 95 Toán 9 Tập 2: Nhà khoa học cổ đại Archimèdes đã khám phá ra cách tính diện tích của mặt cầu như sau: Lấy một nửa hình cầu bán kính R và một hình trụ có bán kính đáy R. Dùng sợi dây quấn quanh nửa mặt cầu như Hình 10a, rồi cùng đoạn dây đó người ta quấn quanh hình trụ như Hình 10b thì thấy chiều cao của phần hình trụ được quấn dây bằng bán kính R.

a) Tính theo R diện tích xung quanh của phần hình trụ được quấn dây ở Hình 10b.

b) Từ đó dự đoán diện tích nửa mặt cầu ở Hình 10a.

Khám phá 3 trang 95 Toán 9 Tập 2 Chân trời sáng tạo | Giải Toán 9

Phân Tích Yêu Cầu

Bài tập trang 95, tập 2, sách Toán lớp 9 Chân trời Sáng tạo, bao gồm hai phần chính: Vận dụng 1 và Khám phá 3.

Vận dụng 1: Yêu cầu thực hành gấp một mô hình đèn trang trí hình cầu từ các mảnh giấy. Phần này mang tính hướng dẫn thực hành, giúp học sinh hình dung cách tạo ra hình cầu từ các vật liệu đơn giản. Các bước được mô tả kèm theo hình ảnh minh họa.
Khám phá 3: Đặt ra một bài toán liên quan đến khám phá của Archimedes về mối liên hệ giữa diện tích mặt cầu và diện tích mặt trụ. Cụ thể, bài toán yêu cầu tính diện tích xung quanh của một phần hình trụ có chiều cao bằng bán kính đáy và sau đó dự đoán diện tích của nửa mặt cầu dựa trên sự tương quan được mô tả.

Cả hai phần đều xoay quanh đối tượng hình cầu, một hình khối quen thuộc trong chương trình học.

Kiến Thức/Nền Tảng Cần Dùng

Để giải quyết các bài tập này, học sinh cần nắm vững các kiến thức sau:

Công thức tính diện tích xung quanh hình trụ:
Diện tích xung quanh của một hình trụ được tính bằng công thức:
$S_{xq} = 2 \pi R h$
Trong đó:
- R là bán kính đáy của hình trụ.
- h là chiều cao của hình trụ.
Khái niệm bán kính và đường kính hình cầu:
Hình cầu là một khối hình học được tạo bởi tập hợp các điểm trong không gian cách đều một điểm cho trước (tâm) một khoảng bằng bán kính R.
Đường kính của hình cầu là gấp đôi bán kính: $d = 2R$ .
Quan hệ giữa các đại lượng hình học (theo khám phá của Archimedes):
Archimedes đã tìm ra một mối quan hệ tuyệt vời giữa hình cầu và hình trụ bao quanh nó. Cụ thể, ông chứng minh rằng diện tích bề mặt của một hình cầu bằng đúng diện tích xung quanh của hình trụ có cùng bán kính đáy và chiều cao bằng đường kính của hình cầu đó.
- Diện tích mặt cầu có bán kính R là: $S_{cầu} = 4 \pi R^2</code></li> <li>Diện tích xung quanh hình trụ có bán kính đáy <code>R</code> và chiều cao <code>h = 2R</code> là: <code>[]S_{xq,trụ} = 2 \pi R h = 2 \pi R (2R) = 4 \pi R^2</code></li> </ul> Phát hiện này đã làm Archimedes vô cùng tự hào, ông yêu cầu hình ảnh một hình cầu và hình trụ bao quanh nó được khắc trên bia mộ của mình. </li> </ol> <h2>Hướng Dẫn Giải Chi Tiết</h2> <h3>Vận dụng 1: Chế tạo mô hình đèn trang trí hình cầu</h3> Phần Vận dụng 1 là một bài tập thực hành, hướng dẫn chi tiết cách tạo ra một mô hình hình cầu đơn giản từ giấy. <ul> <li> Bước 1: Chuẩn bị vật liệu. Học sinh cần chuẩn bị các mảnh giấy hình chữ nhật có kích thước: chiều dài 20 cm và chiều rộng 1 cm. Số lượng mảnh giấy tùy thuộc vào độ dày mong muốn của mô hình. </li> <li> Bước 2: Ghép nối các mảnh giấy. Đục lỗ hai đầu của mỗi mảnh giấy. Sau đó, sử dụng các nút (hoặc ghim, băng dính nhỏ) để gắn các mảnh giấy lại với nhau. Cần đảm bảo các mảnh giấy được nối một cách song song và đều đặn để tạo nên cấu trúc ban đầu cho hình cầu. Các hình 9a và 9b mô tả rõ quá trình này. </li> <li> Bước 3: Cố định cấu trúc và tạo độ cong. Ở bước này, chúng ta sử dụng que tre để cố định hai đầu đối diện của các dải giấy đã nối. Thông tin "Cố định hai lỗ bằng que tre có độ dài bằng <code>[]2pi x</code> (khoảng <code>0,6x</code>) với <code>x</code> là khoảng cách giữa hai cái lỗ" có vẻ hơi khó hiểu trong ngữ cảnh thực hành thông thường. Tuy nhiên, ý chính là dùng một vật liệu cứng (que tre) để giữ hai đầu của "khung" giấy, và độ dài này liên quan đến chu vi hoặc chu kỳ sắp xếp của các mảnh giấy khi chúng được tách ra. <code>x</code> ở đây có thể hiểu là bước lặp lại hoặc khoảng cách đều đặn giữa các điểm cố định trên que tre. Phần <code>[]2pi x</code> có thể là một tham số cần được tính toán tùy theo thiết kế. Tuy nhiên, với mục đích tạo hình cầu, việc tách đều các mảnh giấy ra sẽ quan trọng hơn. Hình 9c cho thấy cách que tre được sử dụng. </li> <li> Bước 4: Hoàn thiện mô hình hình cầu. Sau khi cố định cấu trúc ban đầu, nhẹ nhàng tách các mảnh giấy ra và trải đều chúng. Sự sắp xếp đồng đều của các dải giấy này sẽ tạo nên bề mặt cong, hình thành nên một khối hình cầu hoàn chỉnh như mô tả ở Hình 9d. Mẹo thực hành: <ul> <li>Khi đục lỗ, nên đục ở vị trí cách mép giấy một khoảng đều nhau để đảm bảo tính đối xứng.</li> <li>Sử dụng loại nút hoặc ghim có kích thước phù hợp để không làm rách giấy và giữ chặt các mảnh.</li> <li>Khi tách các mảnh giấy ra, cần làm từ từ và đều tay để tránh làm gãy hoặc rách giấy, giúpmô hình giữ được hình dạng cầu đẹpmắt.</li> </ul> Lỗi hay gặp: <ul> <li>Ghép các mảnh giấy không đều, dẫn đến hình cầu bị méo mó.</li> <li>Đục lỗ không thẳng hàng, làm cho việc cố định bằng que tre khó khăn.</li> <li>Tách giấy quá mạnh tay làm hỏng cấu trúc.</li> </ul> </li> </ul> <h3>Khám phá 3: Dự đoán diện tích nửa mặt cầu</h3> Phần này yêu cầu vận dụng kiến thức về hình trụ và mối liên hệ lịch sử với hình cầu. a) Tính theo R diện tích xung quanh của phần hình trụ được quấn dây ở Hình 10b. <ul> <li>Phân tích yêu cầu: Đề bài cho biết chúng ta đang xét một phần hình trụ. Bán kính đáy của hình trụ này là <code>R</code>. Chiều cao của phần hình trụ được quấn dây là bằng bán kính <code>R</code>.</li> <li>Áp dụng công thức: Ta sử dụng công thức tính diện tích xung quanh hình trụ: <code>[]S_{xq} = 2 \pi R h</code></li> <li>Thay số và tính toán: Với bán kính đáy là <code>R</code> và chiều cao <code>h = R</code>, ta thay vào công thức: <code>[]S_{xq} = 2 \pi R \times R$
 $S_{xq} = 2 \pi R^2$
- Kết quả: Vậy, diện tích xung quanh của phần hình trụ được quấn dây ở Hình 10b là $2 \pi R^2$ .
b) Từ đó dự đoán diện tích nửa mặt cầu ở Hình 10a.
- Phân tích yêu cầu: Đề bài dẫn dắt ta dựa vào khám phá của Archimedes. Ông đã dùng sợi dây quấn quanh nửa mặt cầu (Hình 10a) và sau đó dùng cùng đoạn dây đó quấn quanh hình trụ (Hình 10b). Quan sát cho thấy chiều cao phần hình trụ được quấn dây bằng bán kính R của hình trụ đó.
- Liên hệ kiến thức: Theo mô tả, độ dài sợi dây dùng để quấn nửa mặt cầu (ở Hình 10a) là tương đương với độ dài sợi dây dùng để quấn phần hình trụ có chiều cao R (ở Hình 10b). Điều này ngụ ý rằng diện tích bề mặt của nửa mặt cầu có thể bằng với diện tích xung quanh của phần hình trụ được tính ở câu a).
- Dự đoán: Dựa trên kết quả tính toán ở câu a) là $2 \pi R^2$ , chúng ta có thể dự đoán rằng diện tích của nửa mặt cầu ở Hình 10a là $2 \pi R^2$ .
 Lưu ý: Khám phá gốc của Archimedes còn sâu sắc hơn: ông chỉ ra rằng diện tích toàn bộ mặt cầu (4 pi R^2) bằng diện tích xung quanh của hình trụ bao quanh nó (có bán kính R và chiều cao 2R). Bài toán này đã đơn giản hóa một chút, tập trung vào mối quan hệ khi chiều cao hình trụ bằng bán kính, từ đó suy ra diện tích nửa mặt cầu.
 Mẹo kiểm tra:
 - Luôn nhớ đơn vị của diện tích là đơn vị vuông (ví dụ: cm^2, m^2).
 - Các công thức toán học có thể được kiểm tra lại bằng cách thay các giá trị cụ thể của R và tính toán.
 Lỗi hay gặp:
 - Nhầm lẫn giữa bán kính (R) và đường kính (2R).
 - Áp dụng sai công thức diện tích xung quanh hình trụ hoặc diện tích mặt cầu.
 - Hiểu sai mối quan hệ được mô tả trong phần “Khám phá”, dẫn đến dự đoán sai.
Đáp Án/Kết Quả
Vận dụng 1:
Học sinh thực hiện các bước theo hướng dẫn trong Hình 9 để tự tay làm mô hình đèn trang trí hình cầu. Kết quả là một mô hình có dạng hình cầu được tạo ra từ các dải giấy.
Khám phá 3:
a) Diện tích xung quanh của phần hình trụ được quấn dây là $2 \pi R^2$ .
b) Dự đoán diện tích nửa mặt cầu là $2 \pi R^2$ .
Tổng Kết
Bài tập giải toán 9 trang 95 tập 2 của sách Chân trời Sáng tạo đã mang đến hai hoạt động ý nghĩa. Vận dụng 1 giúp học sinh phát huy tính sáng tạo và kỹ năng thực hành thông qua việc chế tạo mô hình hình cầu, từ đó cảm nhận trực quan về hình khối này. Khám phá 3 lại đưa chúng ta trở về với những phát kiến toán học kinh điển của Archimedes, giúp học sinh thấy được mối liên hệ thú vị giữa hình cầu và hình trụ, cũng như tầm quan trọng của việc suy luận và dự đoán trong toán học. Nắm vững các kiến thức nền tảng về hình học và công thức tính toán là chìa khóa để giải quyết các bài tập tương tự một cách hiệu quả.
Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông
Thầy Đông
Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.