Giải Bài Tập Toán Lớp 8 Bài 1: Hình Hộp Chữ Nhật
Giải bài tập Toán lớp 8 tập 2 bài 1 trang 96, 97 là nội dung bài viết chi tiết giúp các em học sinh nắm vững kiến thức về hình hộp chữ nhật. Bài viết cung cấp lời giải đầy đủ, bám sát chương trình sách giáo khoa, kèm theo hình ảnh minh họa và giải thích cặn kẽ từng bước.
Đề Bài
Video Giải bài tập Toán lớp 8 hay, chi tiếtLời giải
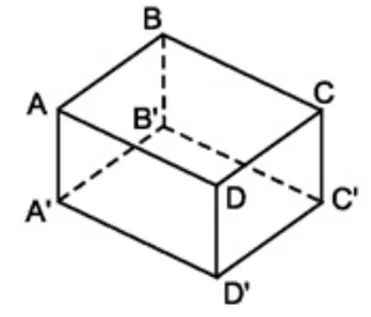
– Các mặt của hình hộp chữ nhật ABCD.A’B’C’D’ bao gồm:
- Mặt đáy trên: A’B’C’D’
- Mặt đáy dưới: ABCD
- Các mặt bên: ABB’A’, CDD’C’, ADD’A’, BCC’B’.
– Các đỉnh của hình hộp chữ nhật ABCD.A’B’C’D’ bao gồm:
- Các đỉnh ở mặt đáy dưới: A, B, C, D
- Các đỉnh ở mặt đáy trên: A’, B’, C’, D’
– Các cạnh của hình hộp chữ nhật ABCD.A’B’C’D’ bao gồm:
- Các cạnh ở mặt đáy dưới: AB, BC, CD, DA
- Các cạnh ở mặt đáy trên: A’B’, B’C’, C’D’, D’A’
- Các cạnh nối hai mặt đáy (cạnh bên): AA’, BB’, CC’, DD’
Giải bài 1 trang 96 SGK Toán 8 Tập 2 | Giải toán lớp 8Hình 72
Lời giải:
Hình hộp chữ nhật ABCD.MNPQ có các cạnh bằng nhau theo từng nhóm:
- Nhóm cạnh thứ nhất (chiều dài): AB = CD = PQ = MN. Đây là các cạnh song song và bằng nhau tạo thành hình chữ nhật ở hai mặt đáy.
- Nhóm cạnh thứ hai (chiều rộng): AD = QM = PN = CB. Đây là các cạnh song song và bằng nhau tạo thành hình chữ nhật ở hai mặt đáy.
- Nhóm cạnh thứ ba (chiều cao): AM = BN = CP = DQ. Đây là các cạnh nối hai mặt đáy, song song và bằng nhau.
Mỗi nhóm bao gồm 4 cạnh có độ dài bằng nhau.
Bài 2 trang 96 SGK Toán 8 Tập 2 : ABCD.A 1 B 1 C 1 D 1 là một hình hộp chữ nhật (h.73).
a) Nếu O là trung điểm của đoạn CB 1 thì O có là điểm thuộc đoạn BC 1 hay không?
b) K là điểm thuộc cạnh CD, liệu K có thể là điểm thuộc cạnh BB 1 hay không?
Giải bài 2 trang 96 SGK Toán 8 Tập 2 | Giải toán lớp 8Hình 73
Lời giải:
Xét hình hộp chữ nhật ABCD.A 1 B 1 C 1 D 1:
a) Nếu O là trung điểm của đoạn CB 1 thì O có là điểm thuộc đoạn BC 1 hay không?
Trong hình hộp chữ nhật, mỗi mặt bên là một hình chữ nhật. Do đó, mặt BCC 1 B 1 là một hình chữ nhật. Hai đường chéo của hình chữ nhật là CB 1 và BC 1. Theo tính chất hình chữ nhật, hai đường chéo cắt nhau tại trung điểm của mỗi đường. Vì O là trung điểm của CB 1, mà hai đường chéo CB 1 và BC 1 cắt nhau tại trung điểm của chúng, nên O cũng là trung điểm của BC 1. Do đó, O là một điểm thuộc đoạn BC 1.
b) K là điểm thuộc cạnh CD, liệu K có thể là điểm thuộc cạnh BB 1 hay không?
Cạnh CD thuộc mặt đáy ABCD. Cạnh BB 1 là một cạnh bên, nối mặt đáy ABCD với mặt đáy A 1 B 1 C 1 D 1. Điểm K thuộc cạnh CD nằm trên mặt phẳng chứa đáy ABCD. Điểm thuộc cạnh BB 1 nằm trên đường thẳng chứa cạnh BB 1. Để K vừa thuộc CD vừa thuộc BB 1, thì K phải là giao điểm của đường thẳng CD và đường thẳng BB 1. Tuy nhiên, hai đường thẳng này song song với nhau hoặc chéo nhau trong không gian ba chiều, và chúng không bao giờ cắt nhau (trừ trường hợp đặc biệt là chúng trùng nhau, nhưng ở đây không phải). Cụ thể, cạnh CD nằm trên mặt phẳng đáy, còn cạnh BB 1 là đường thẳng vuông góc với mặt phẳng đáy (nếu xét theo quy ước thông thường của hình hộp). Do đó, điểm K thuộc cạnh CD thì không thể đồng thời là điểm thuộc cạnh BB 1.
Lời giải:
Cho hình hộp chữ nhật ABCD.A 1 B 1 C 1 D 1 với các kích thước:
- DC = 5 cm
- CB = 4 cm
- BB 1 = 3 cm
Ta cần tìm độ dài DC 1 và CB 1.
Do ABCD.A 1 B 1 C 1 D 1 là hình hộp chữ nhật, nên các mặt bên của nó là hình chữ nhật. Cụ thể, mặt DCC 1 D 1 và mặt CBB 1 C 1 là các hình chữ nhật.
Từ đó suy ra:
- CC 1 = BB 1 = 3 cm (các cạnh đối diện trong hình chữ nhật CBB 1 C 1)
- DC = A 1 D 1 = B 1 C 1 = 5 cm (các cạnh đối diện trong hình chữ nhật DCC 1 D 1 và ABCD)
- CB = D 1 A 1 = B 1 C 1 = A 1 B 1 = 4 cm (các cạnh đối diện trong hình chữ nhật CBB 1 C 1 và ABCD)
Tính độ dài DC 1:
Xét mặt DCC 1 D 1, đây là một hình chữ nhật. Do đó, tam giác DCC 1 vuông tại C.
Áp dụng định lý Py-ta-go cho tam giác vuông DCC 1:
DC_1^2 = DC^2 + CC_1^2
Thay số liệu vào:
DC_1^2 = 5^2 + 3^2
DC_1^2 = 25 + 9
DC_1^2 = 34
Lấy căn bậc hai hai vế:
DC_1 = \sqrt{34} cm
Tính độ dài CB 1:
Xét mặt CBB 1 C 1, đây là một hình chữ nhật. Do đó, tam giác CBB 1 vuông tại B.
Áp dụng định lý Py-ta-go cho tam giác vuông CBB 1:
CB_1^2 = CB^2 + BB_1^2
Thay số liệu vào:
CB_1^2 = 4^2 + 3^2
CB_1^2 = 16 + 9
CB_1^2 = 25
Lấy căn bậc hai hai vế:
CB_1 = \sqrt{25}
CB_1 = 5 cm
Vậy, độ dài DC 1 là \sqrt{34} cm và độ dài CB 1 là 5 cm.
Giải bài 4 trang 97 SGK Toán 8 Tập 2 | Giải toán lớp 8Hình 74
Hãy điền thêm vào hình 74b các mũi tên như vậy.
Lời giải:
Hình lập phương có 6 mặt, và tất cả các mặt đều là hình vuông bằng nhau. Để ghép các mặt của hình lập phương, chúng ta có thể tưởng tượng như sau:
- Chọn một hình vuông làm mặt đáy (ví dụ: hình vuông ở giữa trong hình 74a).
- Các hình vuông xung quanh có thể được gấp lên để tạo thành 4 mặt bên.
- Hình vuông còn lại sẽ được gấp lên để tạo thành mặt đỉnh.
Trong hình 74b, chúng ta cần xác định các mũi tên chỉ hướng gấp các mặt xung quanh lên để tạo thành hình lập phương khi đã có mặt đáy cố định.
Giả sử hình vuông ở giữa là mặt đáy dưới. Các mũi tên sẽ chỉ việc gấp các hình vuông liền kề (trái, phải, trên, dưới so với hình vuông ở giữa) hướng lên trên. Hình vuông ở trên cùng (tương ứng với mũi tên chỉ lên) sẽ là mặt đỉnh. Tương tự, các hình vuông ở hai bên sẽ gấp lên tạo thành các mặt bên còn lại.
Mô phỏng việc điền mũi tên:
- Chọn một hình vuông làm mặt đáy (ví dụ hình A).
- Các hình vuông liền kề với hình A (ví dụ B, C, D, E) sẽ được gấp lên theo hướng mũi tên.
- Nếu hình vuông A là đáy, các hình vuông B, C, D, E sẽ gấp lên tạo thành 4 mặt bên. Hình vuông F ở trên cùng (trong trường hợp các hình vuông được sắp xếp theo hàng ngang hoặc dọc) sẽ gấp lên tạo thành mặt đỉnh.
Dựa trên cách sắp xếp thông thường của hình khai triển hình lập phương, các mũi tên sẽ hướng từ các mặt bên vào mặt đáy và từ các mặt bên vào mặt đỉnh.
Kiến Thức Cần Nhớ Về Hình Hộp Chữ Nhật
Để giải các bài tập về hình hộp chữ nhật, học sinh cần nắm vững các khái niệm và tính chất sau:
- Định nghĩa: Hình hộp chữ nhật là một hình lăng trụ đứng có đáy là hình chữ nhật.
- Các yếu tố:
- Mặt: Hình hộp chữ nhật có 6 mặt, mỗi mặt là một hình chữ nhật. Các mặt đối diện song song và bằng nhau.
- Đỉnh: Có 8 đỉnh.
- Cạnh: Có 12 cạnh. Các cạnh được chia thành 3 nhóm theo 3 kích thước: chiều dài, chiều rộng và chiều cao. Các cạnh trong mỗi nhóm song song và bằng nhau.
- Các kích thước:
- Chiều dài (thường ký hiệu là a hoặc p).
- Chiều rộng (thường ký hiệu là b hoặc q).
- Chiều cao (thường ký hiệu là c hoặc h).
- Đường chéo:
- Đường chéo của mặt: Là đường chéo của các hình chữ nhật tạo thành các mặt.
- Đường chéo của hình hộp chữ nhật: Là đoạn thẳng nối hai đỉnh đối diện không nằm trên cùng một mặt. Hình hộp chữ nhật có 4 đường chéo bằng nhau.
- Công thức tính:
- Diện tích xung quanh: S_{xq} = 2(a+b) \times c
- Diện tích toàn phần: S<em>{tp} = S</em>{xq} + 2 S_{đáy} = 2(ab + ac + bc)
- Thể tích: V = a \times b \times c
- Định lý Py-ta-go trong hình hộp chữ nhật:
- Độ dài đường chéo một mặt (ví dụ mặt đáy): d_{mặt}^2 = a^2 + b^2
- Độ dài đường chéo của hình hộp chữ nhật: d_{hình}^2 = a^2 + b^2 + c^2
Phân Tích Yêu Cầu Bài Tập
Các bài tập về hình hộp chữ nhật thường xoay quanh việc nhận diện các yếu tố (mặt, đỉnh, cạnh), tính toán diện tích (xung quanh, toàn phần) và thể tích, hoặc áp dụng định lý Py-ta-go để tính độ dài đường chéo.
- Bài tập nhận diện: Yêu cầu liệt kê các mặt, đỉnh, cạnh dựa trên hình vẽ hoặc mô tả. Học sinh cần quan sát kỹ hình, phân biệt các mặt, các đỉnh và các cạnh theo đúng quy ước đặt tên.
- Bài tập tính toán: Cần xác định rõ các kích thước (chiều dài, chiều rộng, chiều cao) và áp dụng công thức tương ứng. Đối với các bài toán yêu cầu tính đường chéo, cần xác định xem đó là đường chéo của mặt hay đường chéo của hình hộp, sau đó áp dụng định lý Py-ta-go.
- Bài tập suy luận: Các câu hỏi như bài 2 đòi hỏi học sinh phải vận dụng tính chất của hình hộp chữ nhật và hình chữ nhật để đưa ra lập luận chính xác về vị trí tương đối của các điểm, đường thẳng hoặc mặt phẳng.
Hướng Dẫn Giải Chi Tiết
Mẹo kiểm tra: Khi làm các bài tập về hình hộp chữ nhật, đặc biệt là các bài tính toán, hãy luôn kiểm tra xem các kích thước có hợp lý với nhau không. Ví dụ, đường chéo của hình hộp chữ nhật phải luôn lớn hơn bất kỳ kích thước nào của nó (chiều dài, chiều rộng, chiều cao).
Lỗi hay gặp:
- Nhầm lẫn giữa đường chéo mặt và đường chéo hình hộp chữ nhật.
- Áp dụng sai công thức tính diện tích hoặc thể tích.
- Quên mất hình hộp chữ nhật có 6 mặt là hình chữ nhật, dẫn đến sai lầm khi áp dụng định lý Py-ta-go.
- Không đọc kỹ đề bài, nhầm lẫn các ký hiệu kích thước.
Bài viết này cung cấp cái nhìn tổng quan về hình hộp chữ nhật, bao gồm các định nghĩa, tính chất và cách giải các dạng bài tập thường gặp. Việc nắm vững lý thuyết và luyện tập thường xuyên sẽ giúp các em học sinh tự tin chinh phục các dạng bài toán liên quan đến hình hộp chữ nhật, nâng cao kỹ năng giải toán và tư duy hình học.
Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông
Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.
