Đề thi học sinh giỏi các môn - chuyên đề bồi dưỡng HSG miễn phí

Giải Toán Hình Thang Lớp 5 Cánh Diều: Lý Thuyết và Bài Tập Chi Tiết

by · January 7, 2026

Rate this post

Chào mừng các em học sinh lớp 5 đến với chuyên mục giải toán hình thang theo sách Cánh Diều. Trong bài viết này, chúng ta sẽ cùng nhau tìm hiểu chi tiết về giải toán hình thang lớp 5, từ định nghĩa, đặc điểm cơ bản đến các dạng bài tập thường gặp. Mục tiêu là giúp các em nắm vững kiến thức và tự tin chinh phục mọi dạng toán liên quan đến hình thang. Chúng ta sẽ tập trung vào việc hiểu bản chất, phương pháp giải và cách trình bày lời giải một cách khoa học, chính xác.

Đề Bài

Câu 1
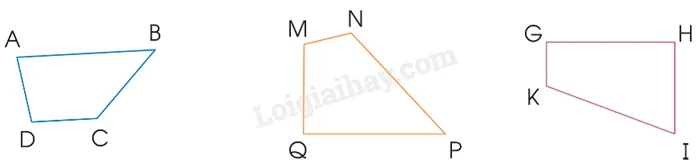
Trong các hình sau, hình nào là hình thang? Hãy chỉ ra cặp cạnh đáy, cặp cạnh bên của mỗi hình thang đó.

Câu 2
Đo chiều cao của mỗi hình thang sau:

Câu 3
a) Hình thang ABCD có những góc nào là góc vuông? Cạnh bên nào vuông góc với hai đáy?

b) Chỉ ra hình thang vuông trong các hình thang sau:

Câu 4
a) Lấy một mảnh giấy hình chữ nhật và một mảnh giấy hình tam giác đặt chồng lên nhau. Quan sát và nói cho bạn nghe phần chồng lên nhau của hai mảnh giấy có hình dạng như thế nào.

b) Cắt hai hình thang giống nhau, rồi ghép thành một hình bình hành.

Nhận xét về mối liên hệ giữa độ dài hai đáy của hình thang với cạnh của hình bình hành.

c) Kể một số vật trong thực tế có dạng hình thang.

Câu 5
a) Chỉ ra cách vẽ thêm hai đoạn thẳng trong mỗi hình sau để được một hình thang:

b) Chỉ ra cách vẽ thêm một đoạn thẳng trong hình sau để được một hình bình hành và một hình tam giác:

Câu 6
a) Vẽ mỗi hình sau vào vở (theo mẫu):

b) Vẽ thêm một đoạn thẳng trong hình 1 để được hai hình thang.

c) Vẽ thêm một đoạn thẳng trong hình 2 để được một hình thang và một hình tam giác.

Phân Tích Yêu Cầu

Các bài tập trong phần này tập trung vào việc nhận biết hình thang, phân biệt các bộ phận của hình thang (đáy, cạnh bên), đo đạc chiều cao, nhận diện hình thang vuông và hiểu mối quan hệ giữa hình thang với các hình khác như hình bình hành thông qua các hoạt động thực hành. Bài tập yêu cầu vận dụng cả kiến thức lý thuyết và kỹ năng quan sát, đo vẽ.

Kiến Thức/Nền Tảng Cần Dùng

Để giải quyết các bài tập về hình thang, chúng ta cần nắm vững các khái niệm sau:

  1. Định nghĩa Hình thang: Hình thang là một tứ giác có một cặp cạnh đối diện song song.

    • Hai cạnh song song được gọi là hai cạnh đáy (thường là đáy lớn và đáy bé).
    • Hai cạnh còn lại được gọi là hai cạnh bên.

  2. Chiều cao Hình thang: Chiều cao của hình thang là độ dài đoạn thẳng vuông góc kẻ từ một đáy xuống đáy kia.

  3. Hình thang vuông: Là hình thang có một góc vuông. Đặc điểm quan trọng là cạnh bên vuông góc với hai đáy chính là chiều cao của hình thang đó.

  4. Các hình liên quan:

    • Hình bình hành: Là tứ giác có hai cặp cạnh đối diện song song và bằng nhau.
    • Hình chữ nhật: Là hình bình hành có bốn góc vuông.
    • Hình tam giác: Là hình có ba cạnh.

Việc hiểu rõ các định nghĩa này sẽ giúp chúng ta xác định đúng hình dạng, đặc điểm và thực hiện các phép đo, vẽ theo yêu cầu của đề bài.

Hướng Dẫn Giải Chi Tiết

Chúng ta sẽ đi sâu vào giải chi tiết từng câu hỏi để các em có thể học hỏi và áp dụng.

Câu 1: Nhận biết hình thang và các bộ phận

Phân tích: Đề bài yêu cầu xác định hình nào là hình thang trong một tập hợp các hình đã cho và chỉ ra cặp cạnh đáy, cạnh bên của các hình thang đó.

Phương pháp giải:

  • Quan sát từng hình.
  • Kiểm tra xem hình đó có một cặp cạnh đối diện song song hay không. Nếu có, đó là hình thang.
  • Xác định cặp cạnh song song (cạnh đáy) và hai cạnh còn lại (cạnh bên).

Lời giải chi tiết:

Dựa vào định nghĩa hình thang (có một cặp cạnh đối diện song song), chúng ta quan sát các hình:

  • Hình A, B, E không có cặp cạnh đối diện nào song song, nên chúng không phải là hình thang.
  • Hình C (ABCD) có cạnh AB song song với cạnh DC. Do đó, ABCD là hình thang.
    • Cặp cạnh đáy: AB và DC.
    • Cặp cạnh bên: AD và BC.
  • Hình D (GHIK) có cạnh GK song song với cạnh HI. Do đó, GHIK là hình thang.
    • Cặp cạnh đáy: GK và HI.
    • Cặp cạnh bên: GH và KI.

Mẹo kiểm tra: Dùng thước và êke hoặc quan sát kỹ các đường thẳng, xem chúng có vẻ song song với nhau không.

Lỗi hay gặp: Nhầm lẫn giữa cạnh đáy và cạnh bên, hoặc không nhận ra cặp cạnh song song.

Câu 2: Đo chiều cao hình thang

Phân tích: Đề bài yêu cầu đo chiều cao của ba hình thang cho sẵn.

Phương pháp giải:

  • Nhớ lại định nghĩa chiều cao hình thang: đoạn thẳng kẻ vuông góc từ một đáy xuống đáy kia.
  • Sử dụng thước kẻ để đo độ dài của các đoạn thẳng này.

Lời giải chi tiết:

Để đo chiều cao, chúng ta cần tìm đoạn thẳng vuông góc nối hai đáy. Quan sát các hình vẽ, chiều cao đã được vẽ sẵn bằng nét đứt và đánh dấu góc vuông.
a) Hình thang có chiều cao là 3 cm.
b) Hình thang có chiều cao là 1,5 cm.
c) Hình thang có chiều cao là 2 cm.

Mẹo kiểm tra: Đảm bảo thước đo được đặt vuông góc với hai đường thẳng song song (hai đáy).

Lỗi hay gặp: Đo sai độ dài hoặc đo xiên, không vuông góc.

Câu 3: Nhận diện hình thang vuông

Phân tích: Bài toán gồm hai phần: xác định góc vuông và cạnh bên vuông góc với hai đáy trong hình thang ABCD; và nhận diện các hình thang vuông trong một nhóm hình cho sẵn.

Phương pháp giải:

  • Hình thang vuông là hình thang có một góc vuông. Cạnh bên tạo với hai đáy góc vuông chính là cạnh bên vuông góc với hai đáy.
  • Quan sát các góc của hình thang.

Lời giải chi tiết:

a) Xét hình thang ABCD:

  • Ta thấy góc tại đỉnh A (angle A) và góc tại đỉnh D (angle D) đều là góc vuông (ký hiệu góc vuông).
  • Do đó, cạnh bên AD vuông góc với hai đáy AB và DC.

b) Chỉ ra hình thang vuông trong các hình thang đã cho:

  • Hình thang ABCD: Có góc angle A và angle D là góc vuông. Vậy ABCD là hình thang vuông.
  • Hình thang EFGH: Không có góc vuông nào.
  • Hình thang KIHS: Có góc angle K và angle H là góc vuông. Vậy KIHS là hình thang vuông.
  • Hình thang LMNO: Không có góc vuông nào.

Mẹo kiểm tra: Tìm các góc có ký hiệu hình vuông hoặc có cạnh thẳng đứng với cạnh nằm ngang.

Lỗi hay gặp: Nhầm lẫn giữa góc vuông và góc tù/nhọn.

Câu 4: Thực hành với hình thang

Phân tích: Câu hỏi này khuyến khích học sinh thực hiện các hoạt động thực tế để hiểu rõ hơn về hình thang.
a) Quan sát phần chồng chéo của hai mảnh giấy.
b) Ghép hai hình thang giống nhau thành hình bình hành và nhận xét.
c) Tìm các vật có dạng hình thang trong thực tế.

Phương pháp giải:

  • Thực hiện các thao tác cắt, ghép, đặt cạnh.
  • Quan sát kết quả và đưa ra nhận xét dựa trên kiến thức đã học.

Lời giải chi tiết:

a) Khi đặt chồng một mảnh giấy hình chữ nhật và một mảnh giấy hình tam giác (sao cho một cạnh của tam giác trùng hoặc cắt một phần của cạnh hình chữ nhật), phần chồng lên nhau thường có hình dạng là một hình thang. Điều này xảy ra khi cạnh của tam giác không song song với cạnh còn lại của hình chữ nhật.

b) Khi lấy hai hình thang giống hệt nhau và ghép lại sao cho cạnh bên của hình này nối với cạnh bên của hình kia, ta sẽ tạo thành một hình bình hành.
Nhận xét: Khi ghép hai hình thang giống nhau, tổng độ dài hai đáy của mỗi hình thang (đáy lớn + đáy bé) sẽ bằng độ dài cạnh của hình bình hành được tạo thành. Cụ thể, nếu hình thang có đáy lớn là a và đáy bé là b, thì hai cạnh của hình bình hành được tạo thành sẽ có độ dài lần lượt là a và b.

c) Một số vật trong thực tế có dạng hình thang:

  • Cái thang: Các bậc thang thường song song, hai thanh dọc hai bên tạo thành hình thang.
  • Mặt bàn hoặc ghế: Một số loại có mặt hình thang.
  • Thùng rác: Nhiều loại thùng rác hình trụ hoặc hình hộp có miệng lớn hơn đáy.
  • Túi đựng bỏng ngô, khoai tây chiên: Thường có đáy nhỏ hơn miệng túi.
  • Mái nhà: Một số phần mái nhà có dạng hình thang.
  • Cửa sổ, cửa ra vào: Một số kiến trúc thiết kế có dạng này.

Mẹo kiểm tra: Quan sát các vật xung quanh và thử hình dung xem chúng có đặc điểm hai cạnh song song, hai cạnh còn lại không song song hay không.

Lỗi hay gặp: Liệt kê các vật không có dạng hình thang rõ ràng.

Câu 5: Vẽ hình thang và hình bình hành

Phân tích: Bài tập yêu cầu vẽ thêm các đoạn thẳng để biến đổi các hình cho trước thành hình thang hoặc hình bình hành.

Phương pháp giải:

  • Nhớ lại định nghĩa hình thang (một cặp cạnh song song) và hình bình hành (hai cặp cạnh song song).
  • Vẽ thêm các đoạn thẳng sao cho thỏa mãn điều kiện song song.

Lời giải chi tiết:

a) Để vẽ thêm hai đoạn thẳng tạo thành hình thang:

  • Hình thứ nhất (tam giác): Ta cần vẽ hai đoạn thẳng từ hai đỉnh của đáy tam giác sao cho chúng song song với nhau và cắt một đường thẳng thứ ba. Hoặc đơn giản hơn, vẽ một đường thẳng song song với cạnh đáy của tam giác.
  • Hình thứ hai (hình chữ nhật): Ta cần vẽ thêm một đường thẳng cắt hai cạnh đối diện của hình chữ nhật sao cho hai đường thẳng mới tạo thành không song song.
(Phần hình ảnh minh họa sẽ được tạo ra theo cách vẽ thêm các đường thẳng song song hoặc cắt các cạnh theo quy tắc). Ví dụ: Từ hai điểm trên một cạnh, vẽ hai đoạn thẳng có hướng và độ dài khác nhau để gặp một đường thẳng ở phía đối diện.

b) Để vẽ thêm một đoạn thẳng tạo thành hình bình hành và một hình tam giác:

  • Ta có một hình chữ nhật. Để tạo ra hình bình hành, ta có thể vẽ một đường chéo. Đường chéo này chia hình chữ nhật thành hai tam giác vuông.
  • Để tạo ra hình bình hành và một hình tam giác từ một hình khác (ví dụ: một tứ giác không phải hình bình hành), ta cần vẽ thêm một đoạn thẳng nối hai đỉnh sao cho tạo ra các cặp cạnh song song.
(Phần hình ảnh minh họa sẽ cho thấy cách vẽ một đường chéo trong hình chữ nhật để tạo thành hai tam giác, hoặc cách vẽ thêm một đoạn thẳng để phân chia một hình phức tạp hơn).

Mẹo kiểm tra: Sau khi vẽ, kiểm tra lại xem hình mới tạo có đúng là hình thang (có cặp cạnh song song) hay hình bình hành (hai cặp cạnh song song) không.

Lỗi hay gặp: Vẽ các đoạn thẳng không song song hoặc sai vị trí.

Câu 6: Vẽ hình theo yêu cầu

Phân tích: Bài tập này yêu cầu học sinh thực hành vẽ hình dựa trên các tính chất của hình thang, hình tam giác và hình bình hành.

Phương pháp giải:

  • Hiểu rõ yêu cầu vẽ.
  • Sử dụng thước và êke để đảm bảo các đường thẳng song song và vuông góc được vẽ chính xác.

Lời giải chi tiết:

a) Vẽ theo mẫu: Học sinh cần quan sát kỹ các hình mẫu trong SGK và vẽ lại chúng vào vở một cách cẩn thận.

b) Vẽ thêm một đoạn thẳng trong hình 1 để được hai hình thang:
Hình 1 ban đầu có thể là một hình đơn giản. Để tạo ra hai hình thang bằng cách thêm một đoạn thẳng, ta cần vẽ đoạn thẳng đó sao cho nó chia hình ban đầu và tạo ra các cặp cạnh song song mới.
Ví dụ: Nếu hình 1 là một hình chữ nhật, ta có thể vẽ một đoạn thẳng nối hai cạnh đối diện nhưng không song song với hai cạnh còn lại, tạo ra hai hình thang. Hoặc nếu hình ban đầu là một tam giác, việc vẽ một đường thẳng song song với đáy sẽ tạo ra một hình thang nhỏ và một hình thang lớn hơn (hoặc một tam giác nhỏ và một hình thang).

(Hình vẽ minh họa sẽ cho thấy cách vẽ đoạn thẳng tạo ra hai hình thang từ hình ban đầu).

c) Vẽ thêm một đoạn thẳng trong hình 2 để được một hình thang và một hình tam giác:
Giả sử hình 2 ban đầu là một hình chữ nhật. Ta có thể vẽ một đường chéo. Đường chéo này sẽ chia hình chữ nhật thành hai hình tam giác vuông. Tuy nhiên, đề bài yêu cầu một hình thang và một hình tam giác.
Một cách khác: Nếu hình 2 ban đầu là một hình tứ giác có hai cạnh đối diện song song (hình thang), ta có thể vẽ thêm một đoạn thẳng chia nó. Hoặc nếu hình 2 là một hình chữ nhật, ta có thể vẽ một đường thẳng cắt hai cạnh không song song với nhau và song song với một cạnh nào đó, để tạo thành một hình thang và một phần còn lại có thể là tam giác hoặc hình thang khác tùy cách vẽ.

(Hình vẽ minh họa sẽ thể hiện cách chia hình ban đầu bằng một đoạn thẳng để có được đúng một hình thang và một hình tam giác).

Mẹo kiểm tra: Sau khi vẽ, hãy dùng thước kiểm tra các cặp cạnh xem chúng có song song với nhau theo đúng yêu cầu của hình thang hoặc hình tam giác không.

Lỗi hay gặp: Vẽ sai, không tạo ra được hình dạng mong muốn, hoặc đoạn thẳng vẽ thêm không đúng vị trí.

Đáp Án/Kết Quả

  • Câu 1: Hình ABCD và GHIK là hình thang. Cặp cạnh đáy và cạnh bên đã được chỉ rõ trong phần giải chi tiết.
  • Câu 2: Chiều cao các hình thang lần lượt là 3 cm, 1,5 cm, và 2 cm.
  • Câu 3:
    a) Hình thang ABCD có angle A và angle D là góc vuông. Cạnh bên AD vuông góc với hai đáy.
    b) Các hình thang vuông là ABCD và KIHS.
  • Câu 4:
    a) Phần chồng chéo có dạng hình thang.
    b) Tổng độ dài hai đáy của hình thang bằng cạnh của hình bình hành ghép từ hai hình thang giống nhau.
    c) Các vật có dạng hình thang bao gồm: cái thang, thùng rác, mặt túi xách,…
  • Câu 5 & 6: Các cách vẽ cụ thể được mô tả chi tiết trong phần hướng dẫn giải, học sinh cần thực hành vẽ lại theo các phương pháp đã nêu.

Conclusion

Việc nắm vững khái niệm và tính chất của hình thang, cùng với việc thực hành giải các bài tập từ cơ bản đến nâng cao, sẽ giúp các em học sinh lớp 5 tự tin hơn khi đối mặt với các dạng toán hình học. Chúc các em luôn học tốt và đạt kết quả cao trong môn Toán với chuyên mục giải toán hình thang lớp 5 này!

Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông

You may also like...

Leave a Reply

Your email address will not be published. Required fields are marked *

Kênh Xoilac TV HD ngon