Giải Toán Lớp 3 Trang 51: Bài Toán Giải Bằng Hai Phép Tính (Tiếp Theo)

by Thầy Đông · January 8, 2026

Rate this post

Chào mừng các em học sinh lớp 3 đến với bài hướng dẫn giải toán lớp 3 trang 51 trong bộ sách Chân trời sáng tạo. Hôm nay, chúng ta sẽ cùng nhau chinh phục các bài tập về bài toán giải bằng hai phép tính, tiếp nối những kiến thức đã học. Mục tiêu của chúng ta là làm rõ cách tiếp cận, phương pháp giải và trình bày lời giải một cách chính xác, giúp các em tự tin làm được các dạng toán tương tự. Hãy cùng nhau làm quen với các bài toán này qua các bước phân tích chi tiết và bài giải mẫu.

Đề Bài

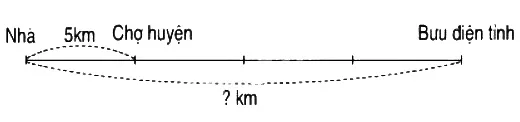
Bài 1: Quãng đường từ nhà đến chợ huyện dài 5 km, quãng đường từ chợ huyện đến bưu điện tỉnh dài gấp ba lần quãng đường từ nhà đến chợ huyện (theo sơ đồ sau). Hỏi quãng đường từ nhà đến bưu điện tỉnh dài bao nhiêu ki-lô-mét?

Giải Toán lớp 3 trang 51

Bài 2: Một thùng đựng 24 lít mật ong, lấy $\frac{1}{3}$ số lít mật ong đó. Hỏi trong thùng còn lại bao nhiêu lít mật ong?

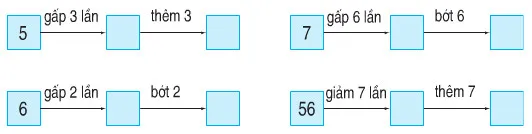
Bài 3: Số?

Toán lớp 3 trang 51 bài 3

Phân Tích Yêu Cầu

Các bài tập trang 51 Toán lớp 3 hôm nay đều xoay quanh chủ đề “Bài toán giải bằng hai phép tính”. Cụ thể:

Bài 1: Yêu cầu tính tổng quãng đường từ nhà đến bưu điện tỉnh. Chúng ta có quãng đường từ nhà đến chợ huyện và mối quan hệ về độ dài giữa quãng đường từ chợ huyện đến bưu điện tỉnh so với quãng đường ban đầu.
Bài 2: Yêu cầu tính số lít mật ong còn lại sau khi đã lấy bớt đi một phần. Chúng ta biết tổng số lít ban đầu và phần đã lấy ra dưới dạng phân số.
Bài 3: Đây là một dạng bài điền số vào chỗ trống, yêu cầu thực hiện các phép tính liên tiếp theo thứ tự từ trái sang phải để tìm ra kết quả cuối cùng.

Việc xác định đúng yêu cầu của từng bài sẽ giúp chúng ta lựa chọn phương pháp giải phù hợp.

Kiến Thức/Nền Tảng Cần Dùng

Để giải quyết các bài toán này, chúng ta cần ôn lại các kiến thức sau:

Nhân với số có một chữ số: Dùng để xác định một đại lượng gấp nhiều lần đại lượng kia. Ví dụ: Gấp 3 lần thì nhân với 3.
$\text{Số mới} = \text{Số cũ} \times \text{Số lần}$
Cộng: Dùng để tính tổng hoặc tìm số lượng gộp lại.
$\text{Tổng} = \text{Số hạng 1} + \text{Số hạng 2}$
Trừ: Dùng để tìm số lượng còn lại sau khi bớt đi hoặc tìm hiệu giữa hai số.
$\text{Số còn lại} = \text{Số ban đầu} - \text{Số bớt đi}$
Chia cho số có một chữ số: Dùng để xác định một phần của đại lượng. Ví dụ: Lấy đi $\frac{1}{3}$ nghĩa là chia cho 3.
$\text{Một phần} = \text{Tổng số} div \text{Mẫu số}$
Thứ tự thực hiện phép tính: Đối với các biểu thức chỉ có phép cộng, trừ, nhân, chia, chúng ta thực hiện theo thứ tự từ trái sang phải.

Hướng Dẫn Giải Chi Tiết

Bài 1: Tính quãng đường từ nhà đến bưu điện tỉnh

Phương pháp giải:

Tìm quãng đường từ chợ huyện đến bưu điện tỉnh.
Tính tổng quãng đường từ nhà đến chợ huyện và từ chợ huyện đến bưu điện tỉnh.

Các bước giải:

Bước 1: Tìm quãng đường từ chợ huyện đến bưu điện tỉnh.
Đề bài cho biết quãng đường từ nhà đến chợ huyện dài 5 km. Quãng đường từ chợ huyện đến bưu điện tỉnh dài gấp ba lần quãng đường đó.
Ta thực hiện phép nhân:
$5 \times 3 = 15 \text{ (km)}$
Vậy, quãng đường từ chợ huyện đến bưu điện tỉnh dài 15 km.
Bước 2: Tính tổng quãng đường từ nhà đến bưu điện tỉnh.
Quãng đường từ nhà đến bưu điện tỉnh là tổng của hai quãng đường: từ nhà đến chợ huyện và từ chợ huyện đến bưu điện tỉnh.
Ta thực hiện phép cộng:
$5 + 15 = 20 \text{ (km)}$
Vậy, quãng đường từ nhà đến bưu điện tỉnh dài 20 km.

Mẹo kiểm tra:
Ta có thể kiểm tra lại bằng cách xem hai quãng đường cộng lại có đúng với kết quả cuối cùng không. Quãng đường từ nhà đến chợ huyện (5 km) cộng với quãng đường từ chợ huyện đến bưu điện tỉnh (15 km) bằng 20 km, khớp với đáp án.

Lỗi hay gặp:

Nhầm lẫn giữa “gấp ba lần” và “gấp ba lần lên” (ví dụ: 5 + 3 = 8 thay vì 5 x 3 = 15).
Chỉ tính ra quãng đường từ chợ huyện đến bưu điện tỉnh mà quên không tính tổng quãng đường.

Đáp án và Lời giải chi tiết:

Quãng đường từ chợ huyện đến bưu điện tỉnh dài là:
$5 \times 3 = 15 \text{ (km)}$

Quãng đường từ nhà đến bưu điện tỉnh dài là:
$5 + 15 = 20 \text{ (km)}$

Đáp số: 20 km

Bài 2: Tính số lít mật ong còn lại

Phương pháp giải:

Tính số lít mật ong đã lấy ra khỏi thùng.
Tính số lít mật ong còn lại trong thùng.

Tóm tắt:

Số lít mật ong ban đầu: 24 lít
Số lít mật ong đã lấy ra: $\frac{1}{3}$ số lít ban đầu
Số lít mật ong còn lại: … lít?

Các bước giải:

Bước 1: Tính số lít mật ong đã lấy ra.
Đề bài cho biết đã lấy ra $\frac{1}{3}$ số lít mật ong. Để tìm số lít mật ong đã lấy ra, ta chia tổng số lít ban đầu cho 3.
Ta thực hiện phép chia:
$24 div 3 = 8 \text{ (lít)}$
Vậy, đã lấy ra 8 lít mật ong.
Bước 2: Tính số lít mật ong còn lại.
Để tìm số lít mật ong còn lại, ta lấy số lít ban đầu trừ đi số lít đã lấy ra.
Ta thực hiện phép trừ:
$24 - 8 = 16 \text{ (lít)}$
Vậy, trong thùng còn lại 16 lít mật ong.

Mẹo kiểm tra:
Số lít đã lấy ra (8 lít) cộng với số lít còn lại (16 lít) có bằng tổng số lít ban đầu không? $8 + 16 = 24$ . Đúng.
Kiểm tra lại phép tính $\frac{1}{3}$ của 24: $24 div 3 = 8$ .

Lỗi hay gặp:

Tính ra số lít đã lấy ra nhưng quên không thực hiện bước trừ để tìm số lít còn lại.
Nhầm lẫn khi chia hoặc trừ.

Đáp án và Lời giải chi tiết:

Số lít mật ong lấy ra là:
$24 div 3 = 8 \text{ (lít)}$

Số lít mật ong còn lại là:
$24 - 8 = 16 \text{ (lít)}$

Đáp số: 16 lít

Bài 3: Điền số vào chỗ trống

Phương pháp giải:
Thực hiện các phép tính theo đúng thứ tự từ trái sang phải để tìm kết quả điền vào các ô trống.

Muốn gấp một số lên nhiều lần ta nhân số đó với số lần.
Muốn giảm một số nhiều lần ta chia số đó cho số lần.
Muốn thêm (bớt) một số đơn vị ta cộng (trừ) số đơn vị.

Các bước giải:

Chúng ta sẽ điền kết quả vào từng ô dựa trên phép tính từ trái sang phải:

Ô đầu tiên: Bắt đầu với số 10.
$10 \times 2 = 20$
Ô đầu tiên điền số 20.
Ô thứ hai: Lấy kết quả vừa tìm được (20) để tiếp tục phép tính.
$20 + 5 = 25$
Ô thứ hai điền số 25.
Ô thứ ba: Lấy kết quả vừa tìm được (25).
$25 \times 3 = 75$
Ô thứ ba điền số 75.
Ô thứ tư: Lấy kết quả vừa tìm được (75).
$75 - 10 = 65$
Ô thứ tư điền số 65.
Ô thứ năm: Lấy kết quả vừa tìm được (65).
$65 div 5 = 13$
Ô thứ năm điền số 13.

Mẹo kiểm tra:
Ta có thể điền ngược lại hoặc tính lại từng bước để đảm bảo kết quả chính xác.

13 nhân 5 bằng 65.
65 cộng 10 bằng 75.
75 chia 3 bằng 25.
25 trừ 5 bằng 20.
20 chia 2 bằng 10.

Lỗi hay gặp:

Thực hiện sai thứ tự phép tính (ví dụ: nhân chia trước, cộng trừ sau, hoặc làm từ phải sang trái).
Nhầm lẫn trong các phép tính cộng, trừ, nhân, chia cơ bản.

Đáp án và Lời giải chi tiết:

Ta thực hiện các phép tính theo chiều từ trái sang phải:

$10 \times 2 = 20$
$20 + 5 = 25$
$25 \times 3 = 75$
$75 - 10 = 65$
$65 div 5 = 13$

Kết quả điền vào các ô trống là: 20, 25, 75, 65, 13.

Đáp Án/Kết Quả

Bài 1: Quãng đường từ nhà đến bưu điện tỉnh dài 20 km.
Bài 2: Trong thùng còn lại 16 lít mật ong.
Bài 3: Các số cần điền lần lượt là: 20, 25, 75, 65, 13.

Hôm nay, chúng ta đã cùng nhau ôn tập và giải chi tiết các bài tập về giải toán lớp 3 trang 51. Bằng cách phân tích yêu cầu, xác định kiến thức nền tảng và thực hiện từng bước giải một cách cẩn thận, các em có thể dễ dàng chinh phục những bài toán tương tự. Hãy nhớ rằng, việc luyện tập thường xuyên và kiểm tra lại kết quả là chìa khóa để nắm vững kiến thức. Chúc các em học tốt!

Ngày chỉnh sửa nội dung mới nhất January 8, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.