Giải Toán Lớp 5 Trang 171 SGK: Đề Bài, Phân Tích và Hướng Dẫn Chi Tiết

Chào mừng các em học sinh lớp 5 đến với chuyên mục giải toán lớp 5 trang 171 SGK Toán 5. Trong bài viết này, chúng ta sẽ cùng nhau khám phá và chinh phục các bài toán về diện tích, tỉ lệ và tiêu thụ xăng, đồng thời trang bị thêm những kiến thức nền tảng vững chắc. Hãy cùng bắt đầu hành trình chinh phục tri thức toán học đầy thú vị này nhé!

Đề Bài

Bài 1 trang 171 SGK Toán 5

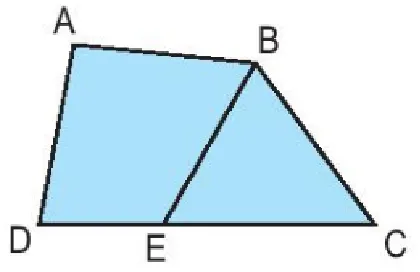
Trên hình bên, diện tích của hình tứ giác ABED lớn hơn diện tích của hình tam giác BEC là (13,6cm^2). Tính diện tích của hình tứ giác ABCD, biết tỉ số diện tích của hình tam giác BEC và diện tích hình tứ giác ABED là (dfrac{2}{3}).

Bài 2 trang 171 SGK Toán 5

Lớp (5A) có (35) học sinh. Số học sinh nam bằng (dfrac{3}{4}) số học sinh nữ. Hỏi số học sinh nữ hơn số học sinh nam là bao nhiêu em ?

Bài 3 trang 171 SGK Toán 5

Một ô tô đi được 100km thì tiêu thụ 12(l) xăng. Ô tô đó đã đi được quãng đường 75km thì tiêu thụ hết bao nhiêu lít xăng ?

Bài 4 trang 171 SGK Toán 5

Hình bên là biểu đồ cho biết tỉ lệ xếp loại học lực của học sinh khối 5 Trường Tiểu học Thắng lợi. Tính số học sinh mỗi loại, biết số học sinh xếp loại học lực khá là 120 học sinh.

Phân Tích Yêu Cầu

Mục tiêu của phần này là hiểu rõ từng bài toán yêu cầu chúng ta tìm kiếm điều gì, các dữ kiện quan trọng đã cho và định hướng phương pháp giải ban đầu.

Bài 1: Tương Quan Diện Tích Hình Học

Bài toán yêu cầu tính diện tích của hình tứ giác ABCD. Chúng ta được cho biết mối quan hệ về hiệu và tỉ số giữa diện tích của hai hình là tứ giác ABED và tam giác BEC. Cụ thể, diện tích tứ giác ABED lớn hơn diện tích tam giác BEC là (13,6cm^2), và tỉ số diện tích giữa tam giác BEC và tứ giác ABED là (dfrac{2}{3}). Để giải bài toán này, chúng ta cần xác định diện tích cụ thể của từng phần (tam giác BEC và tứ giác ABED) dựa trên hiệu và tỉ số đã cho, sau đó cộng chúng lại để được diện tích ABCD.

Bài 2: Tỉ Lệ Số Học Sinh

Bài toán này yêu cầu tìm số học sinh nữ hơn số học sinh nam bao nhiêu em. Chúng ta có tổng số học sinh của lớp 5A là (35) em và mối quan hệ tỉ lệ giữa số học sinh nam và nữ: số học sinh nam bằng (dfrac{3}{4}) số học sinh nữ. Dạng toán này thuộc bài toán tìm hai số khi biết tổng và tỉ số của chúng. Chúng ta cần chia tổng số học sinh thành các phần tương ứng với tỉ lệ đã cho, sau đó tính số học sinh nam, số học sinh nữ và tìm hiệu số giữa hai đối tượng này.

Bài 3: Lượng Tiêu Thụ Xăng Theo Quãng Đường

Bài toán yêu cầu tính lượng xăng tiêu thụ khi ô tô đi được (75km), biết rằng ô tô tiêu thụ (12l) xăng cho (100km). Đây là dạng toán tỉ lệ thuận hoặc bài toán rút về đơn vị. Chúng ta cần xác định lượng xăng tiêu thụ trên mỗi kilômét, sau đó nhân với quãng đường (75km) để tìm ra lượng xăng cần thiết. Việc hiểu rõ mối quan hệ tỉ lệ giữa quãng đường và lượng xăng tiêu thụ là chìa khóa để giải quyết bài toán này một cách chính xác.

Bài 4: Tỉ Lệ Học Lực và Số Lượng

Bài toán này cung cấp biểu đồ về tỉ lệ xếp loại học lực của học sinh khối 5 và cho biết số lượng học sinh xếp loại học lực khá là (120) học sinh. Yêu cầu là tính số học sinh cho từng loại học lực (Giỏi, Khá, Trung bình). Biểu đồ cho thấy các tỉ lệ phần trăm. Chúng ta cần xác định tỉ lệ phần trăm của học sinh khá so với toàn trường. Từ số lượng học sinh khá và tỉ lệ phần trăm của họ, chúng ta có thể tính tổng số học sinh toàn khối 5. Sau khi có tổng số học sinh, chúng ta sẽ tính số lượng học sinh cho mỗi loại còn lại dựa trên tỉ lệ phần trăm tương ứng.

Kiến Thức/Nền Tảng Cần Dùng

Để giải quyết thành công các bài toán này, chúng ta cần nắm vững các kiến thức và phương pháp sau:

1. Giải Bài Toán Tìm Hai Số Khi Biết Hiệu và Tỉ Số

Đây là kiến thức nền tảng cho Bài 1 và Bài 2.

• Hiệu và Tỉ số: Khi biết hiệu và tỉ số của hai số, ta có thể biểu diễn hai số đó dưới dạng các phần bằng nhau theo tỉ số đã cho. Hiệu số giữa hai số sẽ tương ứng với hiệu số phần.
  • Nếu số thứ nhất (lớn hơn) gấp (a) lần số thứ hai (bé hơn), hoặc tỉ số là (dfrac{a}{b}) (với (a > b)), thì hiệu số phần là (a – b).
  • Giá trị của một phần được tính bằng cách lấy hiệu số của hai số chia cho hiệu số phần.
  • Số thứ nhất = Giá trị một phần ( times a ) (hoặc ( times b ) nếu tỉ số là (dfrac{b}{a})).
  • Số thứ hai = Giá trị một phần ( times b ) (hoặc ( times a ) nếu tỉ số là (dfrac{b}{a})).

2. Giải Bài Toán Tìm Hai Số Khi Biết Tổng và Tỉ Số

Đây là phương pháp chính để giải quyết Bài 2.

• Tổng và Tỉ số: Khi biết tổng và tỉ số của hai số, ta coi hai số đó như các phần của một tổng.
  • Tổng số phần bằng nhau = Phần của số thứ nhất + Phần của số thứ hai.
  • Giá trị của một phần = Tổng hai số / Tổng số phần bằng nhau.
  • Số thứ nhất = Giá trị một phần ( times ) số phần của số thứ nhất.
  • Số thứ hai = Giá trị một phần ( times ) số phần của số thứ hai.

3. Giải Bài Toán Rút về Đơn vị

Đây là phương pháp cốt lõi cho Bài 3, giúp tìm ra lượng tiêu thụ cho một đơn vị (ví dụ: 1km) rồi suy ra cho nhiều đơn vị.

• Bước 1: Rút về đơn vị: Tìm giá trị của một đơn vị. Ví dụ, để tìm lượng xăng tiêu thụ cho 1km, ta lấy tổng lượng xăng tiêu thụ chia cho tổng số km đã đi.
  • ( text{Giá trị 1 đơn vị} = text{Tổng giá trị} div text{Số đơn vị} )
• Bước 2: Tìm kết quả: Lấy giá trị của một đơn vị nhân với số đơn vị cần tìm.
  • ( text{Kết quả} = text{Giá trị 1 đơn vị} times text{Số đơn vị cần tìm} )

4. Làm việc với Tỉ lệ Phần trăm

Kiến thức này là cần thiết để giải Bài 4.

• Tổng phần trăm: Tổng tất cả các phần trăm của một tập thể luôn bằng (100%).
• Tìm phần trăm còn lại: Nếu biết tổng phần trăm và một số phần trăm thành phần, ta có thể tìm phần trăm còn lại bằng cách lấy (100%) trừ đi tổng các phần trăm đã biết.
  • ( text{Phần trăm còn lại} = 100% – (text{Phần trăm 1} + text{Phần trăm 2} + ldots) )
• Tìm tổng số lượng khi biết một phần: Nếu biết số lượng tương ứng với một phần trăm nhất định, ta có thể tìm tổng số lượng bằng cách:
  • ( text{Tổng số lượng} = (text{Số lượng đã biết} div text{Phần trăm đã biết}) times 100% )
• Tìm số lượng của một phần: Sau khi có tổng số lượng, ta có thể tìm số lượng của từng phần bằng cách nhân tổng số lượng với tỉ lệ phần trăm của phần đó.
  • ( text{Số lượng phần} = text{Tổng số lượng} div 100% times text{Phần trăm của phần đó} )

Hướng Dẫn Giải Chi Tiết

Bây giờ, chúng ta sẽ đi vào chi tiết từng bước giải cho mỗi bài toán.

Bài 1: Giải Bài 1 trang 171 SGK Toán 5

Phân tích Sơ đồ:

Đề bài cho biết diện tích tứ giác ABED lớn hơn diện tích tam giác BEC là (13,6cm^2) và tỉ số diện tích (text{S}{BEC} : text{S}{ABED} = dfrac{2}{3}).
Ta có thể vẽ sơ đồ đoạn thẳng minh họa mối quan hệ này:

• Diện tích tam giác BEC (phần bé hơn) là 2 phần.
• Diện tích tứ giác ABED (phần lớn hơn) là 3 phần.

Sơ đồ minh họa:

Các bước giải:

1. Tìm hiệu số phần bằng nhau:
   Ta lấy số phần của hình lớn trừ đi số phần của hình bé.
   (3 – 2 = 1) (phần)

2. Tính diện tích hình bé (Tam giác BEC):
   Hiệu (1) phần này tương ứng với (13,6cm^2). Vậy, ta tính diện tích tam giác BEC bằng cách lấy hiệu số đó nhân với số phần của nó.
   (13,6 text{ cm}^2 div 1 times 2 = 27,2 text{ cm}^2)

3. Tính diện tích hình lớn (Tứ giác ABED):
   Có hai cách:

   • Cách 1: Lấy diện tích hình bé cộng với hiệu số.
     (27,2 text{ cm}^2 + 13,6 text{ cm}^2 = 40,8 text{ cm}^2)
   • Cách 2: Lấy giá trị một phần nhân với số phần của nó.
     (13,6 text{ cm}^2 div 1 times 3 = 40,8 text{ cm}^2)

4. Tính diện tích hình tứ giác ABCD:
   Diện tích tứ giác ABCD bằng tổng diện tích của tam giác BEC và diện tích tứ giác ABED.
   (27,2 text{ cm}^2 + 40,8 text{ cm}^2 = 68 text{ cm}^2)

Mẹo kiểm tra:

• Kiểm tra tỉ số diện tích BEC và ABED: (27,2 div 40,8 = 2/3). Đúng.
• Kiểm tra hiệu diện tích: (40,8 – 27,2 = 13,6). Đúng.

Lỗi hay gặp:

• Nhầm lẫn số phần của hai hình trong sơ đồ.
• Quên cộng diện tích của hai phần để ra diện tích hình ABCD.
• Tính sai hiệu số phần hoặc giá trị một phần.

Bài 2: Giải Bài 2 trang 171 SGK Toán 5

Phân tích Sơ đồ:

Đề bài cho biết tổng số học sinh là (35) em. Số học sinh nam bằng (dfrac{3}{4}) số học sinh nữ. Điều này có nghĩa là nếu số học sinh nữ được chia thành 4 phần thì số học sinh nam sẽ chiếm 3 phần.

Sơ đồ minh họa:

• Số học sinh nam: 3 phần
• Số học sinh nữ: 4 phần
• Tổng số học sinh: 7 phần

Các bước giải:

1. Tìm tổng số phần bằng nhau:
   Ta cộng số phần của nam và số phần của nữ.
   (3 + 4 = 7) (phần)

2. Tìm số học sinh nam:
   Tổng số học sinh (35) em tương ứng với (7) phần. Ta tìm số học sinh nam bằng cách lấy tổng số học sinh chia cho tổng số phần, sau đó nhân với số phần của nam.
   (35 text{ học sinh} div 7 times 3 = 15 text{ học sinh})

3. Tìm số học sinh nữ:
   Có hai cách:

   • Cách 1: Lấy tổng số học sinh trừ đi số học sinh nam.
     (35 text{ học sinh} – 15 text{ học sinh} = 20 text{ học sinh})
   • Cách 2: Lấy giá trị một phần nhân với số phần của nữ.
     (35 text{ học sinh} div 7 times 4 = 20 text{ học sinh})

4. Tính số học sinh nữ hơn số học sinh nam:
   Ta lấy số học sinh nữ trừ đi số học sinh nam.
   (20 text{ học sinh} – 15 text{ học sinh} = 5 text{ học sinh})

Mẹo kiểm tra:

• Kiểm tra tỉ lệ nam/nữ: (15 div 20 = 3/4). Đúng.
• Kiểm tra tổng số học sinh: (15 + 20 = 35). Đúng.

Lỗi hay gặp:

• Nhầm lẫn số phần của nam và nữ trong sơ đồ.
• Tính sai giá trị một phần.
• Trả lời sai câu hỏi (ví dụ: chỉ ghi số học sinh nam/nữ mà không tìm hiệu).

Bài 3: Giải Bài 3 trang 171 SGK Toán 5

Tóm tắt:

• Quãng đường: 100 km (rightarrow) Tiêu thụ: 12 lít xăng
• Quãng đường: 75 km (rightarrow) Tiêu thụ: … lít xăng?

Phương pháp giải (Rút về đơn vị):

Chúng ta sẽ tìm lượng xăng tiêu thụ cho 1km trước, sau đó nhân với 75km.

Các bước giải:

1. Tìm số lít xăng tiêu thụ khi đi 1km:
   Chia tổng lượng xăng tiêu thụ cho quãng đường đã đi.
   (12 text{ lít} div 100 text{ km} = 0,12 text{ lít/km})

2. Tìm số lít xăng tiêu thụ khi đi 75km:
   Lấy lượng xăng tiêu thụ cho 1km nhân với quãng đường 75km.
   (0,12 text{ lít/km} times 75 text{ km} = 9 text{ lít})

Đáp số: Ô tô đó đã đi được quãng đường 75km thì tiêu thụ hết 9 lít xăng.

Mẹo kiểm tra:

• Xem xét tỉ lệ. (75km) bằng (dfrac{3}{4}) của (100km). Do đó, lượng xăng tiêu thụ cũng phải bằng (dfrac{3}{4}) của (12l). (12 times dfrac{3}{4} = 9). Kết quả khớp.

Lỗi hay gặp:

• Nhầm lẫn thứ tự phép chia và nhân.
• Tính toán sai phép nhân số thập phân với số tự nhiên.

Bài 4: Giải Bài 4 trang 171 SGK Toán 5

Phân tích Biểu đồ và Yêu cầu:

Biểu đồ cho biết tỉ lệ các loại học lực:

• Học sinh Giỏi: 25%
• Học sinh Khá: (tỉ lệ chưa rõ)
• Học sinh Trung bình: 15%

Chúng ta biết số học sinh Khá là 120 học sinh. Yêu cầu là tính số học sinh mỗi loại.

Các bước giải:

1. Tìm tỉ lệ phần trăm của học sinh Khá:
   Tổng tỉ lệ phần trăm của tất cả các loại học lực là 100%. Ta lấy 100% trừ đi tổng tỉ lệ của học sinh Giỏi và Trung bình.
   (100% – (25% + 15%) = 100% – 40% = 60%)
   Vậy, học sinh Khá chiếm 60% tổng số học sinh toàn khối.

2. Tính tổng số học sinh toàn khối 5:
   Chúng ta biết 60% số học sinh toàn trường là 120 học sinh. Ta tìm tổng số học sinh bằng cách lấy số học sinh Khá chia cho tỉ lệ phần trăm của Khá, rồi nhân với 100%.
   (120 text{ học sinh} div 60% times 100% = 120 div 0,60 = 200 text{ học sinh})

3. Tính số học sinh Giỏi:
   Lấy tổng số học sinh nhân với tỉ lệ phần trăm của học sinh Giỏi.
   (200 text{ học sinh} div 100% times 25% = 200 times 0,25 = 50 text{ học sinh})

4. Tính số học sinh Trung bình:
   Lấy tổng số học sinh nhân với tỉ lệ phần trăm của học sinh Trung bình.
   (200 text{ học sinh} div 100% times 15% = 200 times 0,15 = 30 text{ học sinh})

Đáp số:

• Số học sinh Giỏi: 50 học sinh
• Số học sinh Khá: 120 học sinh (đã cho)
• Số học sinh Trung bình: 30 học sinh

Mẹo kiểm tra:

• Cộng số học sinh của từng loại lại xem có bằng tổng số học sinh toàn khối không: (50 + 120 + 30 = 200). Đúng.
• Kiểm tra lại các tỉ lệ phần trăm: (50/200 = 25%), (120/200 = 60%), (30/200 = 15%). Đúng.

Lỗi hay gặp:

• Tính sai tỉ lệ phần trăm của học sinh Khá.
• Nhầm lẫn giữa số lượng và tỉ lệ phần trăm.
• Thực hiện phép tính sai khi tìm tổng số hoặc số lượng từng loại.

Kết Luận

Qua việc giải chi tiết các bài toán trong trang 171 SGK Toán 5, chúng ta đã cùng nhau ôn lại và củng cố các kiến thức quan trọng về giải toán với hiệu và tỉ số, tổng và tỉ số, bài toán rút về đơn vị, cùng với việc làm việc hiệu quả với tỉ lệ phần trăm. Nắm vững các phương pháp này sẽ giúp các em tự tin hơn khi đối mặt với nhiều dạng bài toán tương tự, phát triển tư duy logic và khả năng giải quyết vấn đề. Hãy tiếp tục luyện tập để chinh phục mọi thử thách trong học tập nhé!

Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.