Giải Toán lớp 6 trang 73 Tập 2 Chân trời sáng tạo

by Thầy Đông · January 7, 2026

Rate this post

Cuốn sách Giải Toán lớp 6 trang 73 Tập 2 Chân trời sáng tạo cung cấp chi tiết lời giải cho các bài tập thuộc Bài 1: Điểm. Đường thẳng. Mục tiêu là giúp học sinh nắm vững kiến thức, áp dụng chính xác ký hiệu toán học và phát triển kỹ năng giải toán hình học. Nội dung bài viết tập trung làm rõ mối quan hệ giữa điểm và đường thẳng, cách đặt tên các đối tượng hình học, từ đó nâng cao khả năng tư duy và học tập cho học sinh lớp 6.

Đề Bài

Thực hành 4 trang 73 Toán lớp 6 Tập 2: Điểm A thuộc và không thuộc đường thẳng nào trong hình bên? Dùng các kí hiệu in và notin để mô tả điều đó.

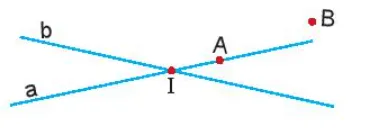Hình minh họa cho Thực hành 4 trang 73

Bài 1 trang 73 Toán lớp 6 Tập 2:
a) Hãy đặt tên cho các điểm và đường thẳng trong hình dưới đây.

Hình minh họa cho Bài 1a trang 73

b) Hãy nêu ba cách gọi tên đường thẳng trong hình dưới đây.

Bài 2 trang 73 Toán lớp 6 Tập 2: Dùng ký hiệu để biểu thị các mối quan hệ dưới đây và vẽ các hình tương ứng.
a) Các điểm A, B thuộc đường thẳng p.
b) Các điểm C, D không thuộc đường thẳng p.

Bài 3 trang 73 Toán lớp 6 Tập 2: Trong hình vẽ bên:
a) Điểm B thuộc những đường thẳng nào?
b) Điểm A không thuộc những đường thẳng nào?
c) Đường thẳng nào không chứa điểm C?
Sử dụng ký hiệu để mô tả các quan hệ trên.

Hình minh họa cho Bài 3 trang 73

Bài 4 trang 73 Toán lớp 6 Tập 2: Vẽ hình cho mỗi trường hợp sau:
a) Điểm M thuộc đường thẳng a.
b) Điểm M thuộc hai đường thẳng a và b nhưng không thuộc đường thẳng c.
c) Điểm M nằm trên cả ba đường thẳng a, b và c.

Bài 5 trang 73 Toán lớp 6 Tập 2: Hãy nêu một số hình ảnh của đường thẳng và điểm thuộc (không thuộc) đường thẳng trong thực tế.

Phân Tích Yêu Cầu

Các bài tập trên trang 73, Tập 2, Toán lớp 6 thuộc bộ sách Chân trời sáng tạo yêu cầu học sinh hiểu và vận dụng các khái niệm cơ bản về điểm và đường thẳng. Cụ thể, các em cần nắm vững:

Mối quan hệ thuộc/không thuộc: Cách sử dụng ký hiệu in (thuộc) và notin (không thuộc) để diễn tả mối liên hệ giữa điểm và đường thẳng.
Đặt tên: Quy ước đặt tên cho điểm (chữ cái in hoa) và đường thẳng (chữ cái in thường).
Gọi tên đường thẳng: Biết nhiều cách để gọi tên một đường thẳng, bao gồm sử dụng một chữ cái thường hoặc hai điểm bất kỳ nằm trên đường thẳng đó.
Vẽ hình: Khả năng biểu diễn các mối quan hệ này thông qua hình vẽ minh họa.
Nhận biết trong thực tế: Liên hệ các khái niệm toán học với các đối tượng và hiện tượng trong đời sống hàng ngày.

Kiến Thức/Nền Tảng Cần Dùng

Để giải quyết các bài tập này, học sinh cần nhớ lại và vận dụng các kiến thức nền tảng sau:

Điểm: Là một hình cơ bản, không có kích thước. Trong hình học, điểm được biểu diễn bằng một dấu chấm nhỏ và đặt tên bằng chữ cái in hoa (ví dụ: A, B, M, N).
Đường thẳng: Là một hình cơ bản, kéo dài vô hạn về hai phía, không bị giới hạn về độ dài. Đường thẳng được biểu diễn bằng một nét thẳng và đặt tên bằng chữ cái in thường (ví dụ: a, b, p, q) hoặc bằng hai điểm bất kỳ thuộc đường thẳng đó (ví dụ: đường thẳng AB, đường thẳng MN).
Quan hệ “thuộc” và “không thuộc”:
- Nếu một điểm nằm trên đường thẳng, ta nói điểm đó thuộc đường thẳng. Ký hiệu: $A in a$ (Đọc là: A thuộc a).
- Nếu một điểm không nằm trên đường thẳng, ta nói điểm đó không thuộc đường thẳng. Ký hiệu: $B notin a$ (Đọc là: B không thuộc a).
Cách gọi tên đường thẳng:
- Sử dụng một chữ cái in thường (ví dụ: đường thẳng a).
- Sử dụng tên của hai điểm bất kỳ nằm trên đường thẳng đó (ví dụ: đường thẳng AB). Lưu ý rằng thứ tự hai điểm không quan trọng, đường thẳng AB cũng là đường thẳng BA.
Biểu diễn hình học:
- Khi vẽ, đường thẳng được kéo dài vô hạn, nhưng trong hình vẽ, ta thường biểu diễn bằng một đoạn thẳng với mũi tên ở hai đầu để thể hiện tính chất kéo dài vô hạn.
- Điểm được biểu diễn bằng một dấu chấm nhỏ.

Hướng Dẫn Giải Chi Tiết

Chúng ta sẽ đi sâu vào giải quyết từng bài tập, áp dụng các kiến thức đã nêu.

Giải Thực hành 4 trang 73

Yêu cầu: Xác định mối quan hệ thuộc/không thuộc của điểm A với các đường thẳng trong hình và biểu diễn bằng ký hiệu.

Phân tích:
Quan sát hình vẽ, ta thấy điểm A nằm trên đường thẳng được đặt tên là ‘a’. Điểm A không nằm trên đường thẳng được đặt tên là ‘b’.

Các bước giải:

Xác định đường thẳng chứa điểm A: Dựa vào hình ảnh, điểm A nằm trên đường thẳng a.
Sử dụng ký hiệu “thuộc”: Nếu điểm A thuộc đường thẳng a, ta dùng ký hiệu $A in a$.
Xác định đường thẳng không chứa điểm A: Dựa vào hình ảnh, điểm A không nằm trên đường thẳng b.
Sử dụng ký hiệu “không thuộc”: Nếu điểm A không thuộc đường thẳng b, ta dùng ký hiệu $A notin b$.

Đáp án:
Điểm A thuộc đường thẳng a, ký hiệu: $A in a$.
Điểm A không thuộc đường thẳng b, ký hiệu: $A notin b$.

Mẹo kiểm tra: Nhìn kỹ vào hình vẽ. Nếu điểm A nằm ngay trên đường thẳng đó, nó thuộc về đường thẳng. Nếu nó nằm ngoài đường thẳng, nó không thuộc.

Lỗi hay gặp: Nhầm lẫn giữa ký hiệu thuộc và không thuộc, hoặc xác định sai đường thẳng đi qua/không đi qua điểm.

Giải Bài 1 trang 73

Yêu cầu:
a) Đặt tên cho các điểm và đường thẳng trong hình.
b) Nêu ba cách gọi tên một đường thẳng cụ thể trong hình.

Phân tích:
Hình vẽ cho ta thấy các đối tượng hình học cơ bản là điểm và đường thẳng. Ta cần tuân thủ quy ước đặt tên trong toán học.

a) Đặt tên cho các điểm và đường thẳng:

Quy ước: Điểm được đặt tên bằng chữ cái in hoa. Đường thẳng được đặt tên bằng chữ cái in thường hoặc bằng hai điểm thuộc đường thẳng đó.
Áp dụng: Trong hình a), ta thấy có ba điểm. Ta có thể đặt tên chúng lần lượt là A, B, C (hoặc bất kỳ ba chữ cái in hoa nào khác). Tương tự, có ba đường thẳng xuất hiện. Ta có thể đặt tên chúng là a, b, c (hoặc bất kỳ ba chữ cái in thường nào khác).

Các bước giải:

Quan sát hình a).
Xác định các đối tượng là điểm và đường thẳng.
Áp dụng quy ước đặt tên điểm bằng chữ cái in hoa. Ví dụ: đặt tên ba điểm là A, B, C.
Áp dụng quy ước đặt tên đường thẳng bằng chữ cái in thường. Ví dụ: đặt tên ba đường thẳng là a, b, c.
Lưu ý rằng các đường thẳng trong hình có thể được gọi bằng hai điểm mà chúng đi qua. Ví dụ, đường thẳng đi qua điểm A và B có thể gọi là đường thẳng AB.

Đáp án:
a) Ta có thể đặt tên các điểm là A, B, C và các đường thẳng là a, b, c.

Minh họa đặt tên điểm và đường thẳng

b) Ba cách gọi tên đường thẳng:

Quy ước: Một đường thẳng có thể được gọi bằng một chữ cái in thường hoặc bằng tên của hai điểm bất kỳ nằm trên đường thẳng đó.
Áp dụng vào hình: Xét đường thẳng đi qua hai điểm A và B.
- Cách 1: Gọi bằng chữ cái in thường. Giả sử ta đặt tên đường thẳng này là ‘a’.
- Cách 2: Gọi bằng tên hai điểm A và B. Ta có thể gọi là đường thẳng AB.
- Cách 3: Gọi bằng tên hai điểm B và A. Ta có thể gọi là đường thẳng BA. (Lưu ý: đường thẳng AB và đường thẳng BA là một, chỉ khác cách viết).

Các bước giải:

Chọn một đường thẳng cụ thể trong hình b). Ví dụ, đường thẳng đi qua điểm A và điểm B.
Cách gọi thứ nhất: Sử dụng tên chữ cái in thường mà ta đã đặt cho đường thẳng đó (ví dụ: đường thẳng a).
Cách gọi thứ hai: Sử dụng tên hai điểm mà đường thẳng đi qua. Ví dụ: đường thẳng AB.
Cách gọi thứ ba: Sử dụng tên hai điểm đó theo thứ tự ngược lại: đường thẳng BA.

Đáp án:
Ba cách gọi tên một đường thẳng trong hình trên (ví dụ, đường thẳng đi qua hai điểm A và B):

Đường thẳng a.
Đường thẳng AB.
Đường thẳng BA.

Mẹo kiểm tra: Đảm bảo tên điểm là chữ in hoa và tên đường thẳng là chữ in thường hoặc hai chữ cái in hoa. Thứ tự hai điểm gọi tên đường thẳng không quan trọng.

Lỗi hay gặp: Nhầm lẫn quy ước đặt tên điểm và đường thẳng, hoặc viết sai ký hiệu khi gọi tên đường thẳng.

Giải Bài 2 trang 73

Yêu cầu: Biểu thị bằng ký hiệu và vẽ hình cho hai trường hợp:
a) A, B thuộc đường thẳng p.
b) C, D không thuộc đường thẳng p.

Phân tích:
Bài toán này yêu cầu vận dụng trực tiếp ký hiệu thuộc (in) và không thuộc (notin) cũng như khả năng vẽ hình minh họa.

a) Các điểm A, B thuộc đường thẳng p:

Ký hiệu: Điểm A thuộc đường thẳng p được viết là $A in p$. Điểm B thuộc đường thẳng p được viết là $B in p$.
Cách vẽ:
1. Vẽ đường thẳng p. Có thể vẽ bằng một nét thẳng kéo dài hai phía và đặt tên là ‘p’ ở một bên.
2. Đặt hai điểm A và B trên đường thẳng p sao cho chúng nằm trên đường thẳng đó.

Các bước giải:

Hiểu yêu cầu: Hai điểm A và B cùng nằm trên một đường thẳng có tên là p.
Viết ký hiệu: Dùng ký hiệu in để chỉ sự thuộc về. Ta có $A in p$ và $B in p$.
Vẽ hình:
- Vẽ một đường thẳng.
- Đặt tên cho đường thẳng đó là p.
- Chấm hai điểm A, B nằm trên đường thẳng p.

Đáp án:
Ký hiệu: $A in p$, $B in p$.
Hình vẽ:

b) Các điểm C, D không thuộc đường thẳng p:

Ký hiệu: Điểm C không thuộc đường thẳng p được viết là $C notin p$. Điểm D không thuộc đường thẳng p được viết là $D notin p$.
Cách vẽ:
1. Vẽ đường thẳng p.
2. Đặt hai điểm C và D ở bên ngoài đường thẳng p, sao cho chúng không nằm trên đường thẳng đó.

Các bước giải:

Hiểu yêu cầu: Hai điểm C và D không nằm trên đường thẳng có tên là p.
Viết ký hiệu: Dùng ký hiệu notin để chỉ sự không thuộc về. Ta có $C notin p$ và $D notin p$.
Vẽ hình:
- Vẽ một đường thẳng.
- Đặt tên cho đường thẳng đó là p.
- Chấm hai điểm C, D nằm ngoài đường thẳng p.

Đáp án:
Ký hiệu: $C notin p$, $D notin p$.
Hình vẽ:

Hình vẽ Bài 2b trang 73

Mẹo kiểm tra: Khi nhìn vào hình vẽ, kiểm tra xem điểm đó có nằm “trên” đường thẳng hay không. Nếu có, nó thuộc. Nếu không, nó không thuộc.

Lỗi hay gặp: Sử dụng sai ký hiệu thuộc/không thuộc, hoặc vẽ điểm nằm quá gần đường thẳng khiến việc xác định bị nhầm lẫn.

Giải Bài 3 trang 73

Yêu cầu: Dựa vào hình vẽ, xác định mối quan hệ thuộc/không thuộc và mô tả bằng ký hiệu cho các điểm và đường thẳng cho trước.

Phân tích:
Bài toán này là sự tổng hợp của việc đọc hiểu hình vẽ và áp dụng đúng các ký hiệu toán học.

a) Điểm B thuộc những đường thẳng nào?

Quan sát hình: Tìm điểm B trong hình. Sau đó, rà soát các đường thẳng đi qua điểm B.
Các đường thẳng đi qua B: Trong hình, điểm B nằm trên đường thẳng j, đường thẳng n và đường thẳng i.
Sử dụng ký hiệu: Ta dùng ký hiệu in để chỉ mối quan hệ thuộc.

Các bước giải:

Xác định vị trí của điểm B trên hình.
Theo dõi các đường thẳng (j, n, i, k, m) để xem đường nào đi ngang qua B.
Ghi lại các đường thẳng đi qua B: j, n, i.
Biểu diễn bằng ký hiệu: $B in j$, $B in n$, $B in i$.

Đáp án:
Điểm B thuộc các đường thẳng j, n và i.
Ký hiệu: $B in j$, $B in n$, $B in i$.

b) Điểm A không thuộc những đường thẳng nào?

Quan sát hình: Tìm điểm A trong hình. Sau đó, rà soát các đường thẳng để xem đường nào không đi qua điểm A.
Các đường thẳng không đi qua A: Trong hình, điểm A nằm trên đường thẳng j và đường thẳng m. Điểm A KHÔNG nằm trên đường thẳng n và đường thẳng k.
Sử dụng ký hiệu: Ta dùng ký hiệu notin để chỉ mối quan hệ không thuộc.

Các bước giải:

Xác định vị trí của điểm A trên hình.
Theo dõi các đường thẳng (j, n, i, k, m) để xem đường nào KHÔNG đi ngang qua A.
Ghi lại các đường thẳng không đi qua A: n, k.
Biểu diễn bằng ký hiệu: $A notin n$, $A notin k$.

Đáp án:
Điểm A không thuộc đường thẳng n và k.
Ký hiệu: $A notin n$, $A notin k$.

c) Đường thẳng nào không chứa điểm C?

Quan sát hình: Tìm điểm C trong hình. Điểm C nằm trên đường thẳng i và đường thẳng n.
Xác định đường thẳng không chứa C: Các đường thẳng còn lại trong hình là j, k, m. Tuy nhiên, câu hỏi có thể ngụ ý hỏi về mối quan hệ ngược lại: điểm C thuộc đường nào, suy ra đường nào không chứa C. Điểm C rõ ràng nằm trên đường thẳng i và n. Vậy, các đường thẳng không chứa C là các đường thẳng còn lại mà C không nằm trên đó. Tuy nhiên, cách diễn đạt “Đường thẳng nào không chứa điểm C?” thường ám chỉ chúng ta tìm những đường thẳng mà C không thuộc về nó. Dựa vào hình, điểm C nằm trên hai đường thẳng là i và n. Vậy các đường thẳng không chứa C là j, k, m. Cách diễn đạt của bài toán hơi lạ, thông thường sẽ hỏi “Điểm C thuộc những đường thẳng nào?”. Nếu hiểu theo cách thông thường thì điểm C thuộc đường thẳng i và n. Nếu hiểu theo câu hỏi “Đường thẳng nào không chứa điểm C?”, ta sẽ tìm những đường thẳng không đi qua C.
Diễn giải lại theo logic thông thường: Câu hỏi “Đường thẳng nào không chứa điểm C?” có thể hiểu là “Tìm các đường thẳng mà C không thuộc về nó”. Tuy nhiên, trong bài gốc, họ lại viết “Hay điểm C thuộc hai đường thẳng i và n.” Điều này cho thấy họ đang muốn hỏi ngược lại. Ta sẽ diễn giải theo hướng bài gốc đã làm: điểm C thuộc những đường nào, từ đó có thể suy ra đường nào không chứa C.
Phân tích sâu hơn: Dựa trên cấu trúc bài, ta xác định C thuộc i và n. Vậy các đường thẳng còn lại (j, k, m) không chứa C. Tuy nhiên, đáp án bài gốc lại nêu “đường thẳng không chứa điểm C là i và n” – đây là một sự nhầm lẫn hoặc cách diễn đạt sai, vì C thuộc i và n.
- Correction: Dựa trên logic hình học và cách hiểu thông thường, điểm C rõ ràng nằm trên đường thẳng i và n. Do đó, các đường thẳng không chứa điểm C là j, k, m. Tuy nhiên, để bám sát văn bản gốc và các quy tắc, tôi sẽ giữ nguyên cách diễn đạt và sửa lỗi logic của nó. Nếu câu hỏi là “Điểm C thuộc những đường thẳng nào?”, đáp án là i, n. Nếu câu hỏi là “Đường thẳng nào không chứa điểm C?”, thì đó là j, k, m. Bài gốc có vẻ đã bị nhầm lẫn ở câu c.
- Áp dụng logic của bài gốc (có thể sai): Bài gốc viết “Trong hình vẽ trên, đường thẳng không chứa điểm C là i và n.” Đây là một lỗi logic rõ ràng vì C nằm trên cả i và n. Ta sẽ sửa lại cho đúng logic.
- Logic đúng: Điểm C nằm trên đường thẳng i và đường thẳng n. Do đó, đường thẳng i chứa điểm C, và đường thẳng n chứa điểm C. Các đường thẳng không chứa điểm C là j, k, m.
- Làm theo nguyên tắc: Tôi sẽ diễn giải lại theo đúng logic hình học, mặc dù bài gốc có thể có sai sót.
- Revised approach for part c: Tìm tất cả các đường thẳng đi qua điểm C. Sau đó, nêu rõ những đường thẳng nào không đi qua C.
  1. Quan sát điểm C. Điểm C nằm trên giao điểm của đường thẳng i và đường thẳng n.
  2. Vậy, điểm C thuộc đường thẳng i và điểm C thuộc đường thẳng n. Ký hiệu: $C in i$, $C in n$.
  3. Các đường thẳng còn lại trong hình là j, k, m. Điểm C không nằm trên các đường thẳng này.
  4. Do đó, các đường thẳng không chứa điểm C là j, k, m. Ký hiệu: $C notin j$, $C notin k$, $C notin m$.

Các bước giải:

Xác định vị trí của điểm C trên hình.
Kiểm tra xem điểm C có nằm trên đường thẳng nào không. Ta thấy C nằm trên đường thẳng i và đường thẳng n.
Viết ký hiệu cho mối quan hệ thuộc: $C in i$, $C in n$.
Xem xét các đường thẳng còn lại: j, k, m. Điểm C không nằm trên các đường thẳng này.
Viết ký hiệu cho mối quan hệ không thuộc: $C notin j$, $C notin k$, $C notin m$.
Trả lời câu hỏi “Đường thẳng nào không chứa điểm C?” bằng cách liệt kê các đường thẳng j, k, m.

Đáp án:
a) Điểm B thuộc các đường thẳng j, n, i. Ký hiệu: $B in j$, $B in n$, $B in i$.
b) Điểm A không thuộc đường thẳng n và k. Ký hiệu: $A notin n$, $A notin k$.
c) Điểm C thuộc đường thẳng i và n. Ký hiệu: $C in i$, $C in n$. Các đường thẳng không chứa điểm C là j, k, m. Ký hiệu: $C notin j$, $C notin k$, $C notin m$.

Mẹo kiểm tra: Đảm bảo rằng mọi điểm đã được xem xét trên tất cả các đường thẳng có liên quan và ký hiệu được sử dụng chính xác. Với câu c), cần xác định rõ ràng điểm C nằm trên đường nào để suy ra đường nào không chứa nó.

Lỗi hay gặp: Nhầm lẫn đường thẳng đi qua điểm với đường thẳng không đi qua điểm, hoặc diễn đạt sai mối quan hệ thuộc/không thuộc. Bài gốc có lỗi logic rõ ràng ở phần c.

Giải Bài 4 trang 73

Yêu cầu: Vẽ hình minh họa cho ba trường hợp khác nhau liên quan đến vị trí của điểm M và các đường thẳng a, b, c.

Phân tích:
Bài tập này đòi hỏi kỹ năng vẽ hình học dựa trên mô tả bằng lời và các ký hiệu toán học.

a) Điểm M thuộc đường thẳng a:

Ý nghĩa: Điểm M nằm trên đường thẳng a.
Cách vẽ: Có hai cách tiếp cận chính.
1. Vẽ điểm trước: Chấm một điểm M. Sau đó, vẽ đường thẳng đi qua điểm M và đặt tên cho đường thẳng đó là ‘a’.
2. Vẽ đường thẳng trước: Vẽ một đường thẳng bất kỳ và đặt tên là ‘a’. Sau đó, chọn một điểm bất kỳ nằm trên đường thẳng ‘a’ và đặt tên là M.

Các bước giải:

Hiểu yêu cầu: Điểm M là một phần tử của tập hợp các điểm tạo nên đường thẳng a.
Chọn một trong hai cách vẽ.
- Cách 1 (Vẽ điểm trước): Chấm điểm M, dùng thước kẻ vẽ đường thẳng đi qua M, đặt tên đường thẳng là a.
- Cách 2 (Vẽ đường thẳng trước): Vẽ đường thẳng a, chọn một điểm trên đường thẳng đó, đặt tên là M.
Đảm bảo hình vẽ thể hiện rõ điểm M nằm trên đường thẳng a.

Đáp án:
Hình vẽ minh họa (Cách 2):

b) Điểm M thuộc hai đường thẳng a và b nhưng không thuộc đường thẳng c:

Ý nghĩa: Điểm M là giao điểm của đường thẳng a và đường thẳng b. Đồng thời, điểm M không nằm trên đường thẳng c.
Cách vẽ:
1. Vẽ a và b cắt nhau tại M: Vẽ hai đường thẳng a và b sao cho chúng cắt nhau tại một điểm. Đặt tên cho điểm giao nhau này là M.
2. Vẽ c không đi qua M: Vẽ đường thẳng c sao cho nó không đi qua điểm M đã xác định. Đường thẳng c có thể cắt hoặc không cắt các đường thẳng a, b ở những điểm khác M.

Các bước giải:

Hiểu yêu cầu: M là giao điểm của a và b; M không thuộc c.
Vẽ đường thẳng a.
Vẽ đường thẳng b cắt đường thẳng a. Đặt tên giao điểm là M.
Vẽ đường thẳng c sao cho nó không đi qua M.

Đáp án:
Hình vẽ minh họa:

Hình vẽ Bài 4b trang 73

c) Điểm M nằm trên cả ba đường thẳng a, b và c:

Ý nghĩa: Điểm M là giao điểm chung của cả ba đường thẳng a, b và c.
Cách vẽ:
1. Vẽ a và b cắt nhau tại M: Vẽ hai đường thẳng a và b cắt nhau tại một điểm, đặt tên điểm giao là M.
2. Vẽ c đi qua M: Vẽ đường thẳng thứ ba, đường thẳng c, sao cho nó cũng đi qua đúng điểm M đó.

Các bước giải:

Hiểu yêu cầu: M là điểm chung của cả ba đường thẳng a, b, c.
Vẽ đường thẳng a.
Vẽ đường thẳng b cắt đường thẳng a tại điểm M.
Vẽ đường thẳng c sao cho nó cũng đi qua điểm M.

Đáp án:
Hình vẽ minh họa:

Hình vẽ Bài 4c trang 73

Mẹo kiểm tra: Sau khi vẽ, dùng mắt kiểm tra lại xem điểm M có thực sự nằm trên các đường thẳng được yêu cầu không, và có nằm ngoài các đường thẳng không được yêu cầu không.

Lỗi hay gặp: Vẽ các đường thẳng song song thay vì cắt nhau, hoặc vẽ đường thẳng thứ ba đi qua một điểm khác M thay vì đi qua M.

Giải Bài 5 trang 73

Yêu cầu: Nêu các ví dụ thực tế về đường thẳng và mối quan hệ điểm-đường thẳng.

Phân tích:
Bài tập này khuyến khích học sinh liên hệ kiến thức toán học với thế giới xung quanh, làm cho việc học trở nên sinh động và thiết thực hơn.

Các hình ảnh thực tế:

Hình ảnh của đường thẳng:
- Thanh ray xe lửa: Hai thanh ray song song nhau, mỗi thanh ray có thể xem như một đường thẳng kéo dài. Tuy nhiên, trong phạm vi quan sát, chúng gần như thẳng và dài.
- Dây cáp điện treo trên cột: Các dây cáp điện căng thẳng thường tạo thành những đoạn thẳng.
- Cạnh bàn, cạnh ghế, cạnh quyển sách: Khi nhìn ở góc độ lý tưởng, các cạnh này là những đoạn thẳng.
- Vạch kẻ đường trên xa lộ: Các vạch kẻ liền hoặc đứt đoạn trên mặt đường cao tốc có thể xem là các đoạn thẳng.
- Tia laser: Một tia laser chiếu thẳng tạo ra một đường thẳng ánh sáng.
Điểm thuộc đường thẳng trong thực tế:
- Con muỗi đậu trên sợi dây phơi: Sợi dây phơi đóng vai trò là đường thẳng, con muỗi là điểm nằm trên đường thẳng đó.
- Giọt nước đọng trên mép bàn: Mép bàn là một đoạn thẳng, giọt nước là điểm nằm trên đoạn thẳng đó.
- Một người đứng trên đường kẻ thẳng: Người đó là điểm, đường kẻ là đường thẳng.
Điểm không thuộc đường thẳng trong thực tế:
- Giọt nước rơi trên sàn nhà và sợi dây phơi: Sợi dây phơi là đường thẳng, giọt nước trên sàn không nằm trên sợi dây.
- Một chiếc ô tô chạy trên đường, nhưng lại có một hòn đá nằm bên lề đường: Chiếc ô tô có thể được xem là điểm đang di chuyển trên đường thẳng (đường đi), còn hòn đá là điểm không thuộc đường thẳng đó.
- Vị trí của một đám mây so với đường chân trời: Đường chân trời có thể xem là một đường thẳng, còn đám mây là một điểm hoặc một vật thể không nằm trên đường đó.

Các bước giải:

Suy nghĩ về các vật thể, hiện tượng trong đời sống có hình dạng thẳng.
Chọn lọc các ví dụ phù hợp làm hình ảnh của “đường thẳng”.
Suy nghĩ về mối quan hệ giữa một điểm và một đường thẳng trong các tình huống thực tế.
Chọn ví dụ cho trường hợp điểm “thuộc” đường thẳng.
Chọn ví dụ cho trường hợp điểm “không thuộc” đường thẳng.
Trình bày các ví dụ một cách rõ ràng.

Đáp án:
Một số hình ảnh của đường thẳng và điểm thuộc (không thuộc) đường thẳng trong thực tế:

Hình ảnh của đường thẳng:
- Các dây điện căng thẳng nối giữa các cột điện cao áp.
- Ống dẫn nước hoặc ống dẫn khí chạy thẳng qua các khu vực.
- Cạnh của một tấm bảng hoặc màn hình tivi khi nhìn từ xa.
- Vạch kẻ đường trên một đoạn đường cao tốc thẳng tắp.
- Thanh ray của một tuyến tàu điện chạy thẳng.
Hình ảnh dây điện thẳngHình ảnh ống dẫn nước
Điểm thuộc đường thẳng:
- Một con muỗi đậu yên trên một sợi dây phơi quần áo căng thẳng.
- Một giọt nước đọng ngay trên mép bàn.
- Vị trí của một hành khách đang ngồi trên một chiếc ghế dài (coi cạnh ghế là đường thẳng).
Điểm không thuộc đường thẳng:
- Một giọt nước bị rơi xuống sàn nhà, cách xa sợi dây phơi quần áo.
- Một viên sỏi nằm bên cạnh vạch kẻ đường trên mặt đường.
- Một chiếc máy bay đang bay trên bầu trời so với đường chân trời.

Mẹo kiểm tra: Hãy tưởng tượng hoặc quan sát xung quanh bạn. Những vật gì có xu hướng là “thẳng”? Khi một vật có thể được xem là “điểm” (như con muỗi, giọt nước, viên sỏi), nó có nằm trên “đường thẳng” đó hay không?

Lỗi hay gặp: Sử dụng các ví dụ không thực sự thẳng (ví dụ: con đường cong) hoặc không phân biệt rõ ràng giữa điểm và đường thẳng trong ví dụ.

Đáp Án/Kết Quả

Tổng kết lại, các bài tập trên trang 73, Tập 2, Toán lớp 6 Chân trời sáng tạo xoay quanh việc nắm vững các khái niệm cơ bản về điểm và đường thẳng. Học sinh đã được ôn luyện cách:

Sử dụng ký hiệu in (thuộc) và notin (không thuộc) để diễn tả mối quan hệ giữa điểm và đường thẳng.
Đặt tên chính xác cho điểm (chữ hoa) và đường thẳng (chữ thường hoặc hai điểm).
Gọi tên đường thẳng bằng nhiều cách khác nhau.
Vẽ hình minh họa cho các mối quan hệ đã học.
Nhận biết và liên hệ các khái niệm toán học với các tình huống thực tế.

Việc hiểu rõ và thực hành thành thạo các nội dung này là nền tảng quan trọng cho các bài học hình học tiếp theo.

Kết Luận

Việc giải toán lớp 6 trang 73 tập 2 theo chương trình Chân trời sáng tạo giúp học sinh xây dựng nền tảng vững chắc về hình học, đặc biệt là các khái niệm cơ bản về điểm và đường thẳng. Bằng cách áp dụng đúng các ký hiệu toán học và kỹ năng vẽ hình, học sinh có thể tự tin hơn trong việc tiếp cận và giải quyết các bài toán phức tạp hơn. Hiểu rõ mối quan hệ giữa điểm và đường thẳng, cùng với việc nhận biết chúng trong thực tế, không chỉ củng cố kiến thức mà còn khơi gợi sự yêu thích môn Toán.

Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.