Giải Toán Lớp 2 Tập 1 Trang 7, 8, 9, 10 Ôn Tập Các Số Đến 100 – Chân Trời Sáng Tạo

Bài viết này cung cấp lời giải chi tiết cho các bài tập Giải Toán Lớp 2 Tập 1 Trang 7, 8, 9, 10 thuộc chủ đề Ôn tập các số đến 100, sách giáo khoa Chân Trời Sáng Tạo. Nhằm giúp các em học sinh lớp 2 nắm vững kiến thức, hiểu rõ cách đọc, viết, so sánh và sắp xếp các số có hai chữ số, cũng như củng cố các khái niệm về hàng chục, hàng đơn vị. Bài viết tập trung vào việc cung cấp phương pháp giải rõ ràng, từng bước cụ thể để học sinh có thể tự mình làm bài tập tương tự.

Đề Bài

Thực hành 1 trang 7 SGK Toán lớp 2 tập 1 – Chân trời sáng tạo:

Bảng các số từ 1 đến 100

Bảng các số từ 1 đến 100

Đọc số

a) Đọc các số theo thứ tự từ 1 đến 100 và ngược lại.

b) Đọc các số tròn chục: 10, 20, ……, 100.

c) Đọc các số cách 5 đơn vị: 5, 10, 15, ……, 100.

Thực hành 2 trang 7 SGK Toán lớp 2 tập 1 – Chân trời sáng tạo:

a) Các số trong bảng được sắp xếp theo thứ tự nào?

b) Các số trong cùng một hàng (không kể số cuối cùng) có gì giống nhau?

c) Các số trong cùng một cột có gì giống nhau?

d) Nhìn hai số bất kì trong cùng một hàng hay cùng một cột, em có thể nói ngay số nào bé hơn và số nào lớn hơn không?

Thực hành 3 trang 8 SGK Toán lớp 2 tập 1 – Chân trời sáng tạo:

So sánh các số.

a) So sánh hai số.

Hình ảnh minh họa so sánh hai số

b) Sắp xếp các số theo thứ tự từ bé đến lớn.

Hình ảnh minh họa sắp xếp các số

Thực hành 4 trang 8 SGK Toán lớp 2 tập 1 – Chân trời sáng tạo:

Làm theo mẫu.

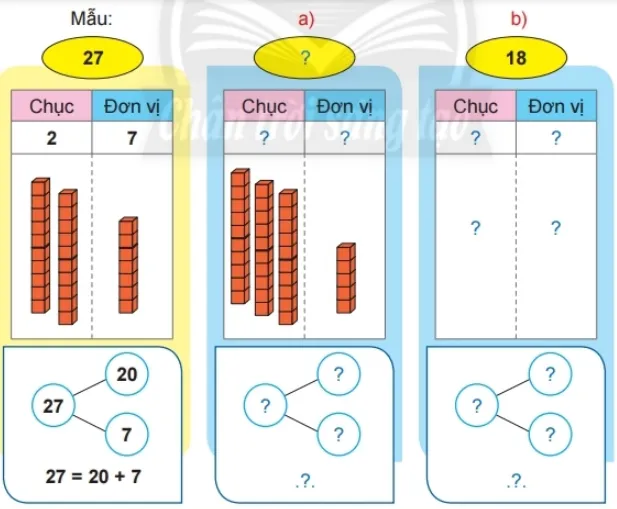Hình ảnh minh họa tách gộp số

Luyện tập 1 trang 9 SGK Toán lớp 2 tập 1 – Chân trời sáng tạo:

Số?

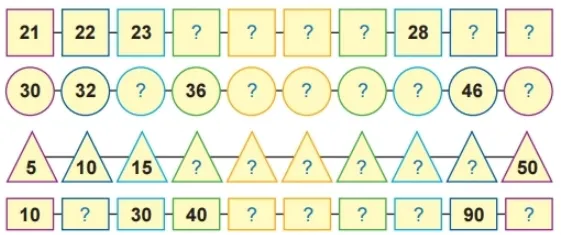Hình ảnh minh họa bài luyện tập 1

Luyện tập 2 trang 9 SGK Toán lớp 2 tập 1 – Chân trời sáng tạo:

Số?

Hình ảnh minh họa bài luyện tập 2

Có …… bạn tham gia trò chơi.

Luyện tập 3 trang 9 SGK Toán lớp 2 tập 1 – Chân trời sáng tạo:

Số?

Người ta có thể dùng chai nhựa đã qua sử dụng để làm chậu trồng cây.

Dưới đây là một số chai, bình bằng nhựa mà bạn Nam đã thu gom được.

Có tất cả bao nhiêu cái?

Hình ảnh minh họa chai nhựa thu gom được

Có tất cả …… cái.

Thử Thách trang 10 SGK Toán lớp 2 tập 1 – Chân trời sáng tạo:

Khay cuối cùng có bao nhiêu cái bánh?

Hình ảnh minh họa Thử Thách

Vui học trang 10 SGK Toán lớp 2 tập 1 – Chân trời sáng tạo:

Tìm phòng giúp các bạn.

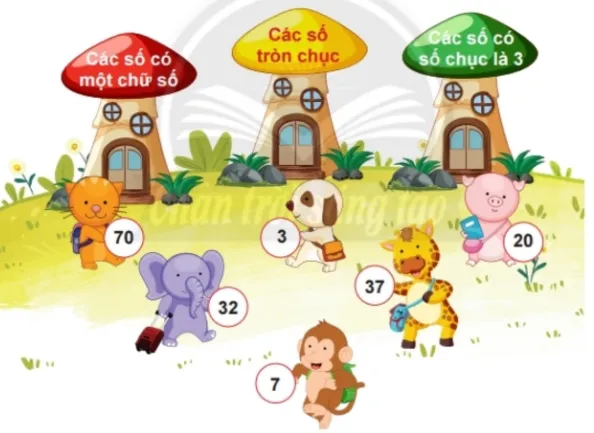Hình ảnh minh họa Vui học

Hoạt động thực tế trang 10 SGK Toán lớp 2 tập 1 – Chân trời sáng tạo:

Cùng người thân chơi trốn tìm để tập đếm: “Năm, mười, mười lăm, hai mươi, ………, một trăm”.

Phân Tích Yêu Cầu

Các bài tập trong phần Giải Toán Lớp 2 Tập 1 Trang 7, 8, 9, 10 chủ yếu xoay quanh việc củng cố và mở rộng hiểu biết về các số có hai chữ số, bao gồm:

• Đọc và viết số: Từ 1 đến 100, số tròn chục, số cách đều 5 đơn vị.
• Cấu tạo số: Xác định chữ số hàng chục, hàng đơn vị và mối quan hệ của chúng trong một số.
• So sánh số: Dựa vào chữ số hàng chục và hàng đơn vị để xác định số lớn hơn hoặc bé hơn.
• Sắp xếp số: Tăng dần hoặc giảm dần theo thứ tự từ bé đến lớn hoặc ngược lại.
• Tách và gộp số: Phân tích một số thành tổng của số chục và số đơn vị, hoặc ngược lại.
• Nhận biết quy luật: Tìm ra quy luật của dãy số để điền số còn thiếu.

Kiến Thức/Nền Tảng Cần Dùng

Để hoàn thành tốt các bài tập này, các em cần nắm vững các kiến thức sau:

1. Hàng của số: Số có hai chữ số gồm chữ số hàng chục và chữ số hàng đơn vị. Chữ số ở bên trái là chữ số hàng chục, chữ số ở bên phải là chữ số hàng đơn vị.
2. Cách đọc số: Đọc chữ số hàng chục rồi đến chữ số hàng đơn vị. Ví dụ: số 35 đọc là “ba mươi lăm”.
3. Cách viết số: Viết chữ số hàng chục trước, sau đó viết chữ số hàng đơn vị. Ví dụ: số “bốn mươi hai” viết là 42.
4. So sánh số có hai chữ số:
   • Nếu hai số có chữ số hàng chục khác nhau, thì số nào có chữ số hàng chục lớn hơn thì số đó lớn hơn.
   • Nếu hai số có chữ số hàng chục giống nhau, thì so sánh chữ số hàng đơn vị. Số nào có chữ số hàng đơn vị lớn hơn thì số đó lớn hơn.
   • Số có hai chữ số luôn lớn hơn số có một chữ số.
5. Tách và gộp số:
   • Tách số thành tổng các số chục và số đơn vị. Ví dụ: 35 = 30 + 5.
   • Gộp số chục và số đơn vị để tạo thành một số. Ví dụ: 10 + 8 = 18.
6. Quy luật dãy số: Quan sát sự thay đổi giữa các số liên tiếp để tìm ra quy luật (ví dụ: hơn kém nhau 1, 2, 5, 10 đơn vị).

Hướng Dẫn Giải Chi Tiết

Thực hành 1 trang 7 SGK Toán lớp 2 tập 1

a) Đọc các số theo thứ tự từ 1 đến 100 và ngược lại:
Các em đọc lần lượt từng số từ 1 đến 100 và ngược lại.
Ví dụ: 1: một, 2: hai, …, 10: mười, 11: mười một, …, 99: chín mươi chín, 100: một trăm.

b) Đọc các số tròn chục:
Các số tròn chục là các số có chữ số hàng đơn vị là 0.
10: mười, 20: hai mươi, 30: ba mươi, 40: bốn mươi, 50: năm mươi, 60: sáu mươi, 70: bảy mươi, 80: tám mươi, 90: chín mươi, 100: một trăm.

c) Đọc các số cách 5 đơn vị:
Bắt đầu từ 5, mỗi số tiếp theo tăng thêm 5 đơn vị.
5: năm, 10: mười, 15: mười lăm, 20: hai mươi, 25: hai mươi lăm, 30: ba mươi, 35: ba mươi lăm, 40: bốn mươi, 45: bốn mươi lăm, 50: năm mươi, 55: năm mươi lăm, 60: sáu mươi, 65: sáu mươi lăm, 70: bảy mươi, 75: bảy mươi lăm, 80: tám mươi, 85: tám mươi lăm, 90: chín mươi, 95: chín mươi lăm, 100: một trăm.

Thực hành 2 trang 7 SGK Toán lớp 2 tập 1

a) Các số trong bảng được sắp xếp theo thứ tự nào?
Quan sát bảng số từ 1 đến 100, ta thấy các số được viết liên tiếp từ trái sang phải, từ trên xuống dưới, theo chiều từ bé đến lớn.
Trả lời: Các số trong bảng được sắp xếp theo thứ tự từ bé đến lớn.

b) Các số trong cùng một hàng (không kể số cuối cùng) có gì giống nhau?
Xem xét một hàng bất kỳ, ví dụ hàng thứ nhất: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Hàng thứ hai: 11, 12, 13, …, 19, 20. Chữ số hàng chục của các số trong cùng một hàng từ 1 đến 10 là 0 (ta coi 1-9 là 01-09), từ 11-19 là 1, từ 21-29 là 2, v.v.
Trả lời: Các số trong cùng một hàng (không kể số cuối cùng) có chữ số hàng chục giống nhau. (Ví dụ: 21, 22, 23, 24, 25, 26, 27, 28, 29 đều có chữ số hàng chục là 2).

c) Các số trong cùng một cột có gì giống nhau?
Xem xét một cột bất kỳ, ví dụ cột đầu tiên: 1, 11, 21, 31, 41, 51, 61, 71, 81, 91. Chữ số hàng đơn vị của các số trong cột này đều là 1. Tương tự, cột thứ hai có chữ số hàng đơn vị là 2.
Trả lời: Các số trong cùng một cột có chữ số hàng đơn vị giống nhau.

d) Nhìn hai số bất kì trong cùng một hàng hay cùng một cột, em có thể nói ngay số nào bé hơn và số nào lớn hơn không?

• Trong cùng một hàng: Số đứng sau luôn lớn hơn số đứng trước vì chữ số hàng đơn vị tăng dần.
• Trong cùng một cột: Số ở phía dưới luôn lớn hơn số ở phía trên vì chữ số hàng chục tăng dần.
  Trả lời: Có. Trong cùng một hàng, số ở ô đằng sau lớn hơn số ở ô đằng trước. Trong cùng một cột, số ở ô bên dưới lớn hơn số ở ô bên trên.

Thực hành 3 trang 8 SGK Toán lớp 2 tập 1

a) So sánh hai số:

• So sánh 79 và 74:
  • Hai số đều có chữ số hàng chục là 7.
  • So sánh chữ số hàng đơn vị: 9 và 4. Vì 9 > 4, nên 79 > 74.
  • Ngược lại, 74 < 79.
• So sánh 52 và 25:
  • Số 52 có chữ số hàng chục là 5. Số 25 có chữ số hàng chục là 2.
  • Vì 5 > 2, nên 52 > 25.
  • Ngược lại, 25 < 52.
    Trả lời:
    79 > 74; 74 < 79
    52 > 25; 25 < 52

b) Sắp xếp các số theo thứ tự từ bé đến lớn:

• Sắp xếp 43, 70, 38:
  • So sánh chữ số hàng chục: 3 của 38, 4 của 43, 7 của 70.
  • Ta có: 3 < 4 < 7.
  • Vậy thứ tự từ bé đến lớn là: 38, 43, 70.
• Sắp xếp 82, 87, 29, 9:
  • Số có một chữ số (9) luôn bé hơn số có hai chữ số.
  • So sánh các số có hai chữ số: 82, 87, 29.
  • Chữ số hàng chục: 8 của 82, 8 của 87, 2 của 29. Ta thấy 2 < 8. Vậy 29 là số bé nhất trong ba số này.
  • So sánh 82 và 87: Chữ số hàng chục đều là 8. So sánh chữ số hàng đơn vị: 2 và 7. Vì 2 < 7, nên 82 < 87.
  • Thứ tự từ bé đến lớn của các số có hai chữ số là: 29, 82, 87.
  • Kết hợp với số có một chữ số: 9, 29, 82, 87.
    Trả lời:
    38; 43; 70
    9; 29; 82; 87

Thực hành 4 trang 8 SGK Toán lớp 2 tập 1

a) Điền số vào sơ đồ tách – gộp:
Hình vẽ cho thấy 3 thanh chục (mỗi thanh là 10) và 5 khối lập phương đơn vị.

• Số chục là 3, số đơn vị là 5.
• Số tạo thành là 35.
• Số 35 có thể tách thành 30 (ba chục) và 5 (năm đơn vị).
• Số 35 = 30 + 5.

b) Điền số vào sơ đồ tách – gộp:
Hình vẽ cho thấy 1 thanh chục (là 10) và 8 khối lập phương đơn vị.

• Số chục là 1, số đơn vị là 8.
• Số tạo thành là 18.
• Số 18 có thể tách thành 10 (một chục) và 8 (tám đơn vị).
• Số 18 = 10 + 8.

Kết quả điền vào sơ đồ:

• Ô chứa hình ảnh 3 thanh chục và 5 đơn vị: Viết số 35. Sơ đồ tách gộp: 35 = 30 + 5.
• Ô chứa hình ảnh 1 thanh chục và 8 đơn vị: Viết số 18. Sơ đồ tách gộp: 18 = 10 + 8.

Luyện tập 1 trang 9 SGK Toán lớp 2 tập 1

Quy luật và cách điền số:

• Hàng hình vuông: Các số hơn kém nhau 1 đơn vị. Để tìm số tiếp theo, cộng thêm 1 vào số trước đó.
  • Ô trống đầu tiên: 1 + 1 = 2.
  • Ô trống thứ hai: 2 + 1 = 3.
  • Ô trống thứ ba: 3 + 1 = 4.
  • Ô trống thứ tư: 4 + 1 = 5.
  • Ô trống thứ năm: 5 + 1 = 6.
  • Ô trống thứ sáu: 6 + 1 = 7.
  • Ô trống thứ bảy: 7 + 1 = 8.
  • Ô trống thứ tám: 8 + 1 = 9.
  • Ô trống thứ chín: 9 + 1 = 10.
• Hàng hình tròn: Các số hơn kém nhau 2 đơn vị. Để tìm số tiếp theo, cộng thêm 2 vào số trước đó.
  • Ô trống đầu tiên: 2 + 2 = 4.
  • Ô trống thứ hai: 4 + 2 = 6.
  • Ô trống thứ ba: 6 + 2 = 8.
  • Ô trống thứ tư: 8 + 2 = 10.
  • Ô trống thứ năm: 10 + 2 = 12.
  • Ô trống thứ sáu: 12 + 2 = 14.
  • Ô trống thứ bảy: 14 + 2 = 16.
  • Ô trống thứ tám: 16 + 2 = 18.
• Hàng hình tam giác: Các số hơn kém nhau 5 đơn vị. Để tìm số tiếp theo, cộng thêm 5 vào số trước đó.
  • Ô trống đầu tiên: 5 + 5 = 10.
  • Ô trống thứ hai: 10 + 5 = 15.
  • Ô trống thứ ba: 15 + 5 = 20.
  • Ô trống thứ tư: 20 + 5 = 25.
  • Ô trống thứ năm: 25 + 5 = 30.
  • Ô trống thứ sáu: 30 + 5 = 35.
  • Ô trống thứ bảy: 35 + 5 = 40.
• Hàng hình chữ nhật: Các số hơn kém nhau 10 đơn vị. Để tìm số tiếp theo, cộng thêm 10 vào số trước đó.
  • Ô trống đầu tiên: 10 + 10 = 20.
  • Ô trống thứ hai: 20 + 10 = 30.
  • Ô trống thứ ba: 30 + 10 = 40.
  • Ô trống thứ tư: 40 + 10 = 50.
  • Ô trống thứ năm: 50 + 10 = 60.
  • Ô trống thứ sáu: 60 + 10 = 70.

Luyện tập 2 trang 9 SGK Toán lớp 2 tập 1

Đếm số bạn tham gia trò chơi:
Trò chơi được chia thành các đội, mỗi đội có 2 bạn. Chúng ta cần đếm tổng số bạn tham gia.
Quan sát hình, có các hàng bạn xếp:

• Hàng trong cùng có 5 cặp bạn, vậy có 5 x 2 = 10 bạn.
• Hàng tiếp theo có 4 cặp bạn, vậy có 4 x 2 = 8 bạn.
  Tổng số bạn tham gia trò chơi là: 10 + 8 = 18 bạn.
  Hoặc có thể đếm tăng dần theo quy luật: 2, 4, 6, 8, 10, 12, 14, 16, 18.
  Trả lời: Có 18 bạn tham gia trò chơi.

Luyện tập 3 trang 9 SGK Toán lớp 2 tập 1

Đếm số chai nhựa:
Các chai nhựa được xếp thành từng nhóm, mỗi nhóm có 5 chai. Chúng ta cần đếm tổng số chai.
Quan sát hình, có các nhóm chai:

• Nhóm 1: 5 chai
• Nhóm 2: 5 chai
• Nhóm 3: 5 chai
• Nhóm 4: 5 chai
• Nhóm 5: 5 chai
• Nhóm 6: 5 chai
• Nhóm 7: 5 chai
  Có 7 nhóm, mỗi nhóm 5 chai. Tổng số chai là: 7 x 5 = 35 cái.
  Hoặc có thể đếm theo quy luật “thêm 5”: Năm, mười, mười lăm, hai mươi, hai mươi lăm, ba mươi, ba mươi lăm.
  Trả lời: Có tất cả 35 cái.

Thử Thách trang 10 SGK Toán lớp 2 tập 1

Tìm số bánh trong khay cuối cùng:
Quan sát dãy số bánh trong các khay: 2, 7, 12, 17, 22.
Ta nhận thấy quy luật của dãy số này là hơn kém nhau 5 đơn vị.

• Từ 2 đến 7: tăng 5 (7 – 2 = 5)
• Từ 7 đến 12: tăng 5 (12 – 7 = 5)
• Từ 12 đến 17: tăng 5 (17 – 12 = 5)
• Từ 17 đến 22: tăng 5 (22 – 17 = 5)
  Để tìm số bánh trong khay cuối cùng (khay thứ sáu), ta lấy số bánh trong khay thứ năm cộng thêm 5.
  Số bánh trong khay thứ sáu = 22 + 5 = 27 cái.
  Trả lời: Khay cuối cùng có 27 cái bánh.

Vui học trang 10 SGK Toán lớp 2 tập 1

Phân loại các bạn theo số:
Chúng ta cần giúp các bạn tìm đúng ngôi nhà dựa trên số của mình.

• Ngôi nhà màu đỏ: Dành cho những bạn mang số có một chữ số.
  • Bạn chó mang số 3 (một chữ số).
  • Bạn khỉ mang số 7 (một chữ số).
• Ngôi nhà màu vàng: Dành cho những bạn mang các số tròn chục.
  • Bạn lợn (heo) mang số 20 (tròn chục).
  • Bạn hổ mang số 70 (tròn chục).
• Ngôi nhà màu xanh: Dành cho những bạn mang các số có chữ số hàng chục là 3.
  • Bạn voi mang số 32 (chữ số hàng chục là 3).
  • Bạn hươu cao cổ mang số 37 (chữ số hàng chục là 3).

Kết quả phân loại:

• Ngôi nhà màu đỏ có: bạn khỉ (số 7), bạn chó (số 3).
• Ngôi nhà màu vàng có: bạn hổ (số 70), bạn lợn (heo) (số 20).
• Ngôi nhà màu xanh có: bạn voi (số 32), bạn hươu cao cổ (số 37).

Đáp Án/Kết Quả

• Thực hành 1: Đọc các số theo yêu cầu.
• Thực hành 2: Các số trong bảng được sắp xếp từ bé đến lớn; các số cùng hàng có chữ số hàng chục giống nhau, các số cùng cột có chữ số hàng đơn vị giống nhau; có thể nói ngay số nào lớn hơn, bé hơn.
• Thực hành 3: a) 79 > 74, 74 < 79, 52 > 25, 25 < 52. b) 38; 43; 70 và 9; 29; 82; 87.
• Thực hành 4: a) Số 35 = 30 + 5. b) Số 18 = 10 + 8.
• Luyện tập 1: Điền các số theo quy luật tăng dần:
  • Hình vuông: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
  • Hình tròn: 2, 4, 6, 8, 10, 12, 14, 16, 18
  • Hình tam giác: 5, 10, 15, 20, 25, 30, 35, 40
  • Hình chữ nhật: 10, 20, 30, 40, 50, 60, 70
• Luyện tập 2: Có 18 bạn tham gia trò chơi.
• Luyện tập 3: Có tất cả 35 cái chai.
• Thử Thách: Khay cuối cùng có 27 cái bánh.
• Vui học: Ngôi nhà đỏ: Khỉ, Chó. Ngôi nhà vàng: Hổ, Lợn. Ngôi nhà xanh: Voi, Hươu cao cổ.
• Hoạt động thực tế: Thực hiện đếm theo chuỗi số với người thân.

Kết luận

Bài học Giải Toán Lớp 2 Tập 1 Trang 7, 8, 9, 10 đã trang bị cho các em những kiến thức cơ bản và quan trọng về các số có hai chữ số. Việc nắm vững cách đọc, viết, so sánh và sắp xếp các số sẽ là nền tảng vững chắc cho các em trong hành trình học tập môn Toán sau này. Hãy thường xuyên ôn tập và thực hành để ghi nhớ kiến thức một cách hiệu quả nhất.

Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.