Giải Toán Lớp 7 Trang 49, 50 Tập 1 Sách Chân Trời Sáng Tạo: Hình Hộp Chữ Nhật và Hình Lập Phương

Chào mừng các em học sinh lớp 7 đến với bài hướng dẫn chi tiết về giải toán lớp 7 trang 49 và giải toán lớp 7 trang 50 trong chương trình sách giáo khoa Chân Trời Sáng Tạo, tập 1. Bài học hôm nay tập trung vào hai khối hình học quen thuộc: hình hộp chữ nhật và hình lập phương. Thông qua các bài tập được giải thích cặn kẽ, các em sẽ nắm vững đặc điểm, tính chất của từng loại hình, từ đó tự tin chinh phục các dạng bài tập tương tự. Chúng ta sẽ cùng đi sâu vào phân tích, lý thuyết và các bước giải cụ thể để mỗi bài toán trở nên dễ hiểu và dễ tiếp cận nhất.

Đề Bài

Bài 1 Trang 49 SGK Toán Lớp 7

Quan sát hình hộp chữ nhật ABCD.EFGH (Hình 10).

a) Nêu các cạnh và đường chéo.

b) Nêu các góc ở đỉnh B và đỉnh C.

c) Kể tên những cạnh bằng nhau.

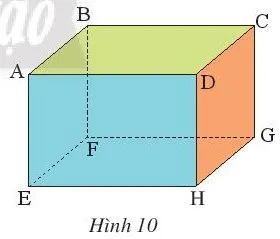Hình minh họa hình hộp chữ nhật ABCD.EFGH

Bài 2 Trang 49 SGK Toán Lớp 7

Quan sát hình lập phương EFGH.MNPQ (Hình 11).

a) Biết MN = 3 cm. Độ dài các cạnh EF, NF bằng bao nhiêu?

b) Nêu tên các đường chéo của hình lập phương.

Hình minh họa hình lập phương EFGH.MNPQ

Bài 3 Trang 50 SGK Toán Lớp 7

Trong các hình dưới đây, hình nào là hình hộp chữ nhật, hình nào là hình lập phương?

Các hình minh họa a, b, c để phân biệt hình hộp chữ nhật và hình lập phương

Bài 4 Trang 50 SGK Toán Lớp 7

Trong hai tấm bìa ở các Hình 13b và Hình 13c, tấm hình nào có thể gấp được hình hộp chữ nhật ở Hình 13a?

Hình minh họa Hình 13a, 13b, 13c về gấp hình hộp chữ nhật

Phân Tích Yêu Cầu

Các bài tập trong phần này đều xoay quanh việc nhận diện, mô tả và phân biệt hai loại khối hình học cơ bản là hình hộp chữ nhật và hình lập phương. Cụ thể:

• Bài 1 & 2: Yêu cầu xác định các thành phần cấu tạo nên hình (cạnh, đường chéo, góc) và nhận biết các cạnh bằng nhau trong từng loại hình.
• Bài 3: Đòi hỏi khả năng phân biệt hình hộp chữ nhật và hình lập phương dựa trên đặc điểm của các mặt.
• Bài 4: Kiểm tra sự hiểu biết về cách “mở phẳng” (khai triển) của hình hộp chữ nhật để có thể gấp lại thành khối hình đó từ các tấm bìa.

Kiến Thức/Nền Tảng Cần Dùng

Để giải quyết các bài toán này, chúng ta cần nắm vững các khái niệm sau:

Hình Hộp Chữ Nhật

• Định nghĩa: Hình hộp chữ nhật là hình có 6 mặt đều là hình chữ nhật.
• Các thành phần:
  • Đỉnh: Là điểm gặp nhau của các cạnh (có 8 đỉnh).
  • Cạnh: Là đoạn thẳng nối hai đỉnh liền nhau trên một mặt hoặc nối các mặt với nhau (có 12 cạnh).
  • Mặt: Là các hình chữ nhật giới hạn khối hình (có 6 mặt).
  • Đường chéo: Là đoạn thẳng nối hai đỉnh không cùng nằm trên một mặt (có 4 đường chéo).
• Tính chất:
  • Có 3 cặp mặt hình chữ nhật bằng nhau.
  • Các cạnh song song và bằng nhau theo từng bộ ba kích thước. Ví dụ, nếu các kích thước là chiều dài, chiều rộng, chiều cao, thì sẽ có 4 cạnh có độ dài chiều dài, 4 cạnh có độ dài chiều rộng, và 4 cạnh có độ dài chiều cao.
  • Các góc tại mỗi đỉnh đều là góc vuông.

Hình Lập Phương

• Định nghĩa: Hình lập phương là trường hợp đặc biệt của hình hộp chữ nhật, trong đó tất cả 6 mặt đều là hình vuông bằng nhau.
• Các thành phần: Tương tự hình hộp chữ nhật (8 đỉnh, 12 cạnh, 6 mặt, 4 đường chéo).
• Tính chất:
  • Tất cả 12 cạnh có độ dài bằng nhau.
  • Cả 6 mặt đều là hình vuông bằng nhau.
  • Các góc tại mỗi đỉnh đều là góc vuông.

Hướng Dẫn Giải Chi Tiết

Bài 1 Trang 49 SGK Toán Lớp 7

a) Nêu các cạnh và đường chéo:

• Các cạnh: Hình hộp chữ nhật có 12 cạnh. Dựa vào hình vẽ, các cạnh này có thể được nhóm lại theo các đường thẳng song song.
  • Nhóm 1 (đáy dưới): AB, BC, CD, DA
  • Nhóm 2 (đáy trên): EF, FG, GH, HE
  • Nhóm 3 (đứng): AE, BF, CG, DH
  • Vậy, 12 cạnh là: AB, BC, CD, DA, EF, FG, GH, HE, AE, BF, CG, DH.
• Đường chéo: Đường chéo nối hai đỉnh không nằm trên cùng một mặt.
  • AG (nối A và G)
  • BH (nối B và H)
  • CE (nối C và E)
  • DF (nối D và F)
  • Vậy, 4 đường chéo là: AG, BH, CE, DF.

b) Nêu các góc ở đỉnh B và đỉnh C:

Mỗi đỉnh của hình hộp chữ nhật là giao điểm của ba mặt, tạo thành ba góc vuông.

• Các góc ở đỉnh B: Ba mặt gặp nhau tại B là mặt ABCD (mặt đáy), mặt ABFE (mặt bên trái), và mặt BCGF (mặt bên trước). Ba góc tạo bởi các cạnh gặp nhau tại B là:
  • Góc $angle ABC$ (trong mặt đáy ABCD)
  • Góc $angle ABF$ (trong mặt bên ABFE)
  • Góc $angle CBF$ (trong mặt bên BCGF)
• Các góc ở đỉnh C: Ba mặt gặp nhau tại C là mặt ABCD (mặt đáy), mặt BCGF (mặt bên trước), và mặt CDHG (mặt bên phải). Ba góc tạo bởi các cạnh gặp nhau tại C là:
  • Góc $angle BCD$ (trong mặt đáy ABCD)
  • Góc $angle BCG$ (trong mặt bên BCGF)
  • Góc $angle DCG$ (trong mặt bên CDHG)

c) Kể tên những cạnh bằng nhau:

Trong hình hộp chữ nhật, các cạnh song song và có cùng vị trí tương đối sẽ bằng nhau.

• Các cạnh có chiều dài (ví dụ: AB, CD): AB = CD = EF = HG.

• Các cạnh có chiều rộng (ví dụ: BC, AD): BC = AD = FG = EH.

• Các cạnh có chiều cao (ví dụ: AE, BF): AE = BF = CG = DH.

• Mẹo kiểm tra: Trong hình hộp chữ nhật, nếu ta gọi độ dài 3 kích thước là $a, b, c$, thì sẽ có 4 cạnh có độ dài $a$, 4 cạnh có độ dài $b$, và 4 cạnh có độ dài $c$.

• Lỗi hay gặp: Nhầm lẫn giữa các cạnh bằng nhau, đặc biệt khi không nhìn rõ hình hoặc không xác định đúng các cạnh song song.

Bài 2 Trang 49 SGK Toán Lớp 7

a) Biết MN = 3 cm. Độ dài các cạnh EF, NF bằng bao nhiêu?

Hình lập phương có tất cả các cạnh bằng nhau. Do đó, nếu biết độ dài một cạnh, tất cả các cạnh còn lại đều có độ dài bằng cạnh đó.

• Vì MN là một cạnh của hình lập phương EFGH.MNPQ, và MN = 3 cm.
• Cạnh EF thuộc mặt trên của hình lập phương và song song với MN.
• Cạnh NF (hoặc FN) là một đường chéo của mặt bên FPNQ. Tuy nhiên, đề bài có thể nhầm lẫn giữa cạnh NF và cạnh FN. Nếu NF là cạnh của hình lập phương, thì nó cũng phải bằng 3 cm. Giả định đề bài muốn hỏi độ dài các cạnh của hình lập phương. Cạnh FN thực chất là một đường chéo của mặt bên FPNQ, không phải là cạnh của hình lập phương. Tuy nhiên, nếu “NF” được hiểu là một cạnh của hình lập phương nối liền N với đỉnh khác, hoặc nếu hình vẽ có cách đặt tên khác, ta cần xem xét kỹ. Dựa vào cách ký hiệu thông thường của hình lập phương, các cạnh là EF, FG, GH, HE, EM, MP, PQ, QN, và các cạnh nối đáy trên với đáy dưới như EN, FP, GQ, HM. Nếu đề bài hỏi cạnh FN, thì đó là đường chéo mặt bên. Nếu đề bài hỏi cạnh FP hoặc GN, thì nó là cạnh đứng. Giả định đề bài có lỗi đánh máy và muốn hỏi một cạnh khác của hình lập phương, ví dụ cạnh FP hoặc GN.
• Tuy nhiên, nếu “NF” được hiểu là cạnh NP hoặc NM hoặc NQ, thì nó bằng 3cm. Nếu là cạnh FN, thì không phải là cạnh hình lập phương.
• Trong ngữ cảnh này, thường đề bài sẽ hỏi các cạnh khác của hình lập phương. Chúng ta sẽ giả định “NF” là một lỗi đánh máy và đề bài muốn hỏi các cạnh cùng độ dài với MN.
• Do đó, EF = 3 cm và nếu “NF” thực sự là một cạnh của hình lập phương thì cũng bằng 3 cm.

b) Nêu tên các đường chéo của hình lập phương:

Đường chéo của hình lập phương nối hai đỉnh đối diện nhau và không cùng nằm trên một mặt.

• Đường chéo nối đỉnh E với đỉnh P: EP

• Đường chéo nối đỉnh F với đỉnh Q: FQ

• Đường chéo nối đỉnh G với đỉnh H: GH (chú ý: G và H nằm trên cùng một mặt, nên GH là cạnh). Cần tìm đỉnh đối diện.

• Đỉnh đối diện với E là P.

• Đỉnh đối diện với F là Q.

• Đỉnh đối diện với G là M. (GM)

• Đỉnh đối diện với H là N. (HN)

• Vậy, 4 đường chéo là: EP, FQ, GM, HN.

• Mẹo kiểm tra: Hình lập phương có 4 đường chéo, mỗi đường chéo nối một đỉnh của mặt này với đỉnh đối diện của mặt kia.

• Lỗi hay gặp: Nhầm lẫn giữa đường chéo của mặt bên và đường chéo của hình lập phương.

Bài 3 Trang 50 SGK Toán Lớp 7

Phân loại hình:

Dựa trên đặc điểm của các mặt:

• Hình hộp chữ nhật: Có 6 mặt là hình chữ nhật. Trong đó có 3 cặp mặt hình chữ nhật bằng nhau. Nếu ba kích thước (dài, rộng, cao) khác nhau, thì các mặt sẽ là 3 cặp hình chữ nhật có kích thước khác nhau. Nếu hai kích thước bằng nhau, thì sẽ có 2 mặt vuông và 4 mặt chữ nhật.
• Hình lập phương: Có 6 mặt đều là hình vuông và bằng nhau. Điều này có nghĩa là ba kích thước dài, rộng, cao của hình lập phương phải bằng nhau.

Áp dụng vào các hình a, b, c:

• Hình a, b: Quan sát các mặt của hình a và hình b, ta thấy các mặt đều là hình chữ nhật. Ba cặp mặt có kích thước khác nhau (ví dụ: một mặt có thể là hình chữ nhật có cạnh 4×3, một mặt 3×1, một mặt 4×1). Do đó, hình a và hình b là hình hộp chữ nhật.

• Hình c: Quan sát hình c, ta thấy tất cả các mặt đều là hình vuông. Các cạnh của hình này đều bằng nhau. Do đó, hình c là hình lập phương.

• Mẹo kiểm tra: Nhìn vào các mặt. Nếu tất cả đều là hình vuông và có kích thước giống nhau thì là hình lập phương. Nếu các mặt là hình chữ nhật (có thể bao gồm cả hình vuông nếu đó là trường hợp đặc biệt), thì là hình hộp chữ nhật.

• Lỗi hay gặp: Nhầm lẫn giữa hình chữ nhật và hình vuông, hoặc không nhận ra hình lập phương là một trường hợp đặc biệt của hình hộp chữ nhật.

Bài 4 Trang 50 SGK Toán Lớp 7

Xác định tấm bìa có thể gấp thành hình hộp chữ nhật:

Để xác định tấm bìa nào có thể gấp thành hình hộp chữ nhật ở Hình 13a, chúng ta cần xem xét “mạng gấp” (khai triển) của hình hộp chữ nhật đó. Hình hộp chữ nhật ở Hình 13a có các kích thước: chiều dài là 4 cm, chiều rộng là 3 cm, và chiều cao là 1 cm.

Một hình hộp chữ nhật có thể được khai triển thành một “mạng” gồm 6 hình chữ nhật. Mạng này phải có cấu trúc sao cho khi gấp lại sẽ tạo thành khối hộp. Cấu trúc phổ biến là một hình chữ nhật lớn làm “thân” (bao gồm 4 mặt bên) và hai hình chữ nhật nhỏ hơn làm “nắp” (mặt đáy và mặt trên).

• Phân tích kích thước hình hộp 13a:

  • Mặt đáy và mặt trên có kích thước: 4 cm x 3 cm.
  • Hai mặt bên cạnh có kích thước: 4 cm x 1 cm.
  • Hai mặt bên còn lại có kích thước: 3 cm x 1 cm.

• Xem xét Hình 13b: Tấm bìa này có thể được coi là khai triển của một hình hộp chữ nhật.

  • Ta thấy có 4 hình chữ nhật 4×1 xếp liền nhau tạo thành một dải dài (tương ứng với 4 mặt bên có chiều cao 1cm).
  • Hai hình chữ nhật 4×3 gắn ở hai đầu của dải 4×1 này.
  • Khi gấp lại, hình 4×3 sẽ trở thành mặt đáy/mặt trên, và dải 4×1 khi gấp lại sẽ tạo thành các mặt bên có chiều cao 1cm và chiều dài 4cm. Chiều rộng của đáy sẽ là 3cm.
  • Vậy, hình 13b có thể gấp thành hình hộp chữ nhật có kích thước 4x3x1.

• Xem xét Hình 13c: Tấm bìa này trông giống như một mạng gấp của hình hộp, nhưng cấu trúc không phù hợp với kích thước của hình 13a.

  • Trong hình 13c, có vẻ như các hình chữ nhật có kích thước là 3×1, 4×1, 3×4, 4×1, 3×1 được sắp xếp.
  • Nếu ta coi hình chữ nhật 4×3 ở giữa là mặt đáy, thì các hình 4×1 và 3×1 gắn vào sẽ tạo thành các mặt bên. Tuy nhiên, cách sắp xếp này không tạo ra được một khối hộp có chiều cao đồng nhất. Hoặc, nếu coi các hình 4×1 và 3×1 làm mặt bên, thì hình 4×3 gắn vào đâu để làm đáy/nắp là không rõ ràng và không khớp với cấu trúc của hình 13a.
  • Cách sắp xếp chuẩn cho hình hộp 4x3x1 thường có 4 mặt bên liền nhau tạo thành một dải, và 2 mặt đáy gắn vào hai bên của dải đó. Hình 13c không có cấu trúc như vậy.

• Kết luận: Tấm bìa ở Hình 13b có thể gấp được hình hộp chữ nhật ở Hình 13a.

• Mẹo kiểm tra: Hãy tưởng tượng hoặc vẽ lại mạng gấp của hình hộp chữ nhật với các kích thước cho trước. Sau đó so sánh với các tấm bìa được cho.

• Lỗi hay gặp: Nhầm lẫn giữa các kích thước, không hình dung được cách gấp hoặc sai lầm trong việc nhận diện mạng gấp của hình khối.

Đáp Án/Kết Quả

• Bài 1:
  • a) Các cạnh: 12 cạnh được liệt kê. Đường chéo: AG, BH, CE, DF.
  • b) Các góc ở đỉnh B: $angle ABC$, $angle ABF$, $angle CBF$. Các góc ở đỉnh C: $angle BCD$, $angle BCG$, $angle DCG$.
  • c) Các cạnh bằng nhau: AB = CD = EF = HG; BC = AD = FG = EH; AE = BF = CG = DH.
• Bài 2:
  • a) EF = 3 cm. Nếu NF là một cạnh của hình lập phương thì NF = 3 cm.
  • b) Các đường chéo: EP, FQ, GM, HN.
• Bài 3:
  • Hình a, b là hình hộp chữ nhật.
  • Hình c là hình lập phương.
• Bài 4: Tấm bìa ở Hình 13b có thể gấp được hình hộp chữ nhật ở Hình 13a.

Bài viết này đã cung cấp hướng dẫn chi tiết cho các bài tập về hình hộp chữ nhật và hình lập phương trong sách giáo khoa Toán lớp 7 Chân Trời Sáng Tạo, trang 49, 50. Bằng cách nắm vững các khái niệm và phương pháp giải, các em học sinh có thể tự tin hoàn thành bài tập và hiểu sâu hơn về các khối hình học cơ bản.

Ngày chỉnh sửa nội dung mới nhất January 8, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.