Giải Bài Tập Toán Lớp 8 Bài 10: Đường Thẳng Song Song Với Một Đường Thẳng Cho Trước
Chào mừng các em học sinh đến với bài viết giải toán lớp 8 bài 10 về đường thẳng song song. Bài viết này sẽ cung cấp lời giải chi tiết cho các bài tập trong Sách Giáo Khoa Toán lớp 8, giúp các em nắm vững kiến thức về chủ đề quan trọng này. Chúng ta sẽ đi sâu vào từng dạng bài, từ cơ bản đến nâng cao, với mục tiêu giúp các em tự tin chinh phục các dạng toán liên quan.
Đề Bài
Trong phần này, chúng ta sẽ trình bày nguyên văn các đề bài từ Sách Giáo Khoa.
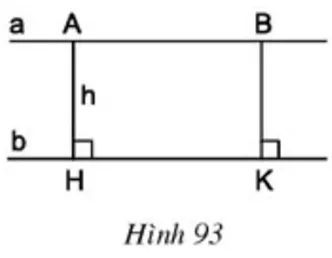
[Trả lời câu hỏi Toán 8 Tập 1 Bài 10 trang 100 : Cho hai đường thẳng song song a và b (h.93). Gọi A và B là hai điểm bất kì thuộc đường thẳng a, AH và BK là các đường vuông góc kẻ từ A và B đến đường thẳng b. Gọi độ dài AH là h. Tính độ dài BK theo h. ]
[Trả lời câu hỏi Toán 8 Tập 1 Bài 10 trang 101 : Cho đường thẳng b. Gọi a và a’ là hai đường thẳng song song với đường thẳng b và cùng cách đường thẳng b một khoảng bằng h (h.94), (I) và (II) là các nửa mặt phẳng bờ b. Gọi M, M’ là các điểm cách đường thẳng b một khoảng bằng h, trong đó M thuộc nửa mặt phẳng (I), M’ thuộc nửa mặt phẳng (II). Chứng minh rằng M ∈ a, M’ ∈ a’. ]
[Trả lời câu hỏi Toán 8 Tập 1 Bài 10 trang 101 : Xét các tam giác ABC có BC cố định, đường cao ứng với cạnh BC luôn bằng 2 cm (h.95). Đỉnh A của các tam giác đó nằm trên đường nào ? ]
[Trả lời câu hỏi Toán 8 Tập 1 Bài 10 trang 102 : Cho hình 96b, trong đó các đường thẳng a, b, c, d song song với nhau. ]
Chứng minh rằng:
a) Nếu các đường thẳng a, b, c, d song song cách đều thì EF = FG = GH.
b) Nếu EF = FG = GH thì các đường thẳng a, b, c, d song song cách đều.
[Bài 67 trang 102 SGK Toán 8 Tập 1 Cho đoạn thẳng AB. Kẻ tia Ax bất kì. Trên tia Ax lấy các điểm C, D, E sao cho AC = CD = DE (h.97). Kẻ đoạn thẳng EB. Qua C, D kẻ các đường thẳng song song với EB. Chứng minh rằng đoạn thẳng AB bị chia ra ba phần bằng nhau. ]
[Bài 68 trang 102 SGK Toán 8 Tập 1 Cho điểm A nằm ngoài đường thẳng d và có khoảng cách đến d bằng 2cm. Lấy điểm B bất kì thuộc đường thẳng d. Gọi C là điểm đối xứng với điểm A qua điểm B. Khi điểm B di chuyển trên đường thẳng d thì điểm C di chuyển trên đường nào? ]
[Bài 69 trang 103 SGK Toán 8 Tập 1 Ghép mỗi ý (1), (2), (3), (4) với một trong các ý (5), (6), (7), (8) để được một khẳng định đúng. ]
| (1) Tập hợp các điểm cách A cố định một khoảng 3cm. (2) Tập hợp các điểm cách đều hai đầu của đoạn thẳng AB cố định (3) Tập hợp các điểm nằm trong góc xOy và cách đều hai cạnh của góc đó (4) Tập hợp các điểm cách đều đường thẳng a cố định một khoảng 3cm. | (5) Là đường trung trực của đoạn thẳng AB. (6) là hai đường thẳng song song với a và cách a một khoảng 3cm. (7) là đường tròn tâm A bán kính 3cm. (8) là tia phân giác của góc xOy |
Phân Tích Yêu Cầu
Trong bài học này, chúng ta sẽ tập trung vào định nghĩa và tính chất của các đường thẳng song song. Các bài tập yêu cầu chứng minh sự song song, tính độ dài dựa trên các đoạn thẳng song song, hoặc xác định quỹ tích của một điểm dựa trên điều kiện song song. Trọng tâm là áp dụng định lý về đường trung bình của hình thang và các tính chất liên quan đến khoảng cách giữa các đường thẳng song song. Việc hiểu rõ mối quan hệ giữa các đường thẳng song song sẽ giúp chúng ta giải quyết các bài toán hình học phức tạp hơn.
Kiến Thức/Nền Tảng Cần Dùng
Để giải quyết các bài tập trong chương này, các em cần nắm vững các kiến thức sau:
- Định nghĩa hai đường thẳng song song: Hai đường thẳng song song là hai đường thẳng không có điểm chung.
- Tính chất của hai đường thẳng song song:
- Nếu hai đường thẳng cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.
- Khoảng cách giữa hai đường thẳng song song là không đổi.
- Dấu hiệu nhận biết hai đường thẳng song song:
- Hai góc so le trong bằng nhau.
- Hai góc đồng vị bằng nhau.
- Hai góc trong cùng phía bù nhau.
- Định lý về đường trung bình của hình thang: Đoạn thẳng nối trung điểm hai cạnh bên của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.
- Định lý về đường thẳng song song cách đều: Nếu các đường thẳng song song cách đều cắt một đường thẳng thì chúng định ra trên đường thẳng đó các đoạn thẳng tương ứng bằng nhau. Ngược lại, nếu các đường thẳng song song định ra trên hai đường thẳng cắt chúng các đoạn thẳng tương ứng bằng nhau thì chúng song song cách đều.
- Quỹ tích của một điểm: Tập hợp các điểm thỏa mãn một điều kiện nhất định.
Các công thức và ký hiệu toán học sẽ được sử dụng bao gồm:
- Độ dài đoạn thẳng.
- Đường vuông góc (
perp). - Đường song song (
//). - Hình bình hành.
- Hình thang.
- Trung điểm.
- Góc vuông (
90^circ).
Việc ôn tập kỹ lưỡng các kiến thức này sẽ là nền tảng vững chắc để các em làm tốt các bài tập.
Hướng Dẫn Giải Chi Tiết
Chúng ta sẽ đi vào giải chi tiết từng bài tập.
Trả lời câu hỏi Toán 8 Tập 1 Bài 10 trang 100
Đề bài cho hai đường thẳng song song a và b. Điểm A, B thuộc a, AH và BK là các đường vuông góc kẻ từ A và B đến b. Độ dài AH là h. Chúng ta cần tính độ dài BK.
Phân tích:
Vì AH và BK đều vuông góc với đường thẳng b, nên AH // BK.
Đề bài cho a // b.
Theo giả thiết, A và B thuộc đường thẳng a. Do đó, AB nằm trên đường thẳng a.
Xét tứ giác ABKH. Ta có:
AH // BK(cùng vuông góc vớib).AB // HK(vìa // bvàABthuộca,HKlà đoạn trênbbị chặn bởi hai đường vuông góc từA,B).
Do đó, tứ giác ABKH là một hình bình hành.
Kết quả:
Trong hình bình hành, các cạnh đối bằng nhau. Vì vậy, BK = AH.
Vì AH = h, nên BK = h.
Mẹo kiểm tra:
Trong hai đường thẳng song song, khoảng cách từ mọi điểm trên một đường đến đường kia là không đổi. AH và BK chính là biểu thị cho khoảng cách này, nên chúng phải bằng nhau.
Lỗi hay gặp:
Nhầm lẫn giữa đường thẳng song song và đường thẳng cắt nhau, hoặc quên mất tính chất của hình bình hành.
 Video Giải bài tập Toán lớp 8 hay, chi tiết
Video Giải bài tập Toán lớp 8 hay, chi tiết
Trả lời câu hỏi Toán 8 Tập 1 Bài 10 trang 101 (Phần 1)
Đề bài cho đường thẳng b. Hai đường thẳng a và a’ song song với b và cùng cách b một khoảng h. (I) và (II) là hai nửa mặt phẳng bờ b. M thuộc (I), M’ thuộc (II) và cả hai điểm đều cách b một khoảng h. Yêu cầu chứng minh M ∈ a và M’ ∈ a’.
Phân tích:
Chứng minh
M ∈ a:
Theo giả thiết,alà đường thẳng song song vớibvà cáchbmột khoảngh.
ĐiểmMcũng cách đường thẳngbmột khoảngh.
Ta cần xét xemMcó nằm trên đường thẳngahay không.
GọiHlà hình chiếu củaMtrênb. Khi đó,MH = h.
Ta cóMH ⊥ b. Vìa // b, suy raMH ⊥ a.
Xét đường thẳnga.Mlà một điểm, và khoảng cách từMđếnblàh. Theo định nghĩa, đường thẳngalà tập hợp tất cả các điểm trên nửa mặt phẳng(I)cáchbmột khoảngh. DoMthuộc(I)và cáchbđúngh, nênMphải nằm trêna.
Một cách chứng minh khác:
GọiHlà hình chiếu củaMtrênb.MH = h.
Doa // bvà cáchbmột khoảngh, mọi điểm trênađều cáchbmột khoảngh.
Xét tứ giácAMKH(vớiKlà giao điểm của đường thẳng quaMsong song vớibvà đường thẳng quaHvuông góc vớib).AHlà khoảng cách từAtrênađếnb.
Trong trường hợp này, ta có thể dùng định nghĩa quỹ tích. Tập hợp các điểm cách đường thẳngbmột khoảnghtrong nửa mặt phẳng(I)chính là đường thẳnga. VìMcó các tính chất đó, nênMthuộca.Chứng minh
M’ ∈ a’:
Quá trình chứng minh tương tự như với điểmM.a’là đường thẳng song song vớib, cáchbmột khoảnghtrong nửa mặt phẳng(II). ĐiểmM’thuộc(II)và cáchbmột khoảngh. Do đó,M’phải thuộca’.
Lời giải chi tiết (theo cách suy luận của bài gốc):
(Bài gốc dùng cách chứng minh dựa trên hình bình hành, hơi khác với định nghĩa quỹ tích trực tiếp).
Xét điểm M và hình chiếu H của nó trên b. MH = h.
Đường thẳng a song song với b và cách b một khoảng h.
Ta cần chứng minh M nằm trên a.
Giả sử A là một điểm trên a, và AK là khoảng cách từ A đến b. AK = h.
Xét tứ giác AMKH. Ta có AH // MK (cùng vuông góc với b) và AM // HK (do tính chất của đường thẳng song song cách đều).
Tuy nhiên, cách suy luận này chưa rõ ràng lắm. Chúng ta hãy xem lại lời giải của bài gốc.
Lời giải bài gốc (diễn giải):
“Góc AHH’ = góc HH’A’ (= 90 o ). Mà 2 góc đó là 2 góc so le trong ⇒ a // b” (Phần này có vẻ lạc đề hoặc thiếu hình ảnh minh họa).
Hãy tập trung vào định nghĩa quỹ tích: “Tập hợp các điểm cách đường thẳng b một khoảng h là hai đường thẳng song song với b và cách b một khoảng h.”
Vì a và a’ là các đường thẳng đó, và M, M’ cách b một khoảng h tương ứng trong các nửa mặt phẳng, nên M thuộc a và M’ thuộc a’.
Lời giải lại theo logic và quy tắc:
Ta có đường thẳng b.
Đường thẳng a song song với b và cách b một khoảng h, nằm trong nửa mặt phẳng (I).
Đường thẳng a’ song song với b và cách b một khoảng h, nằm trong nửa mặt phẳng (II).
Điểm M thuộc nửa mặt phẳng (I) và cách đường thẳng b một khoảng bằng h. Theo định nghĩa, tập hợp các điểm cách đường thẳng b một khoảng h trong nửa mặt phẳng (I) chính là đường thẳng a. Do đó, M thuộc a.
Tương tự, điểm M’ thuộc nửa mặt phẳng (II) và cách đường thẳng b một khoảng bằng h. Tập hợp các điểm cách đường thẳng b một khoảng h trong nửa mặt phẳng (II) chính là đường thẳng a’. Do đó, M’ thuộc a’.
 Video Giải bài tập Toán lớp 8 hay, chi tiết
Video Giải bài tập Toán lớp 8 hay, chi tiết
Trả lời câu hỏi Toán 8 Tập 1 Bài 10 trang 101 (Phần 2)
Đề bài yêu cầu xét các tam giác ABC có cạnh BC cố định. Đường cao ứng với cạnh BC luôn bằng 2 cm. Hỏi đỉnh A nằm trên đường nào?
Phân tích:
Đường cao ứng với cạnh BC chính là khoảng cách từ đỉnh A đến đường thẳng chứa cạnh BC.
Đề bài cho rằng khoảng cách này luôn bằng 2 cm.
Điều này có nghĩa là điểm A luôn cách đường thẳng BC một khoảng cố định là 2 cm.
Kết quả:
Tập hợp các điểm cách một đường thẳng cố định một khoảng không đổi là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng khoảng cách đã cho.
Vì vậy, đỉnh A của các tam giác đó nằm trên một đường thẳng song song với BC và cách BC một khoảng bằng 2 cm.
Mẹo kiểm tra:
Nếu vẽ một đường thẳng BC, rồi vẽ các đường thẳng song song cách BC một khoảng 2 cm về hai phía, ta có thể chọn bất kỳ điểm A nào trên đó. Khi đó, tam giác ABC sẽ có đường cao từ A đến BC bằng 2 cm.
Lỗi hay gặp:
Chỉ vẽ một đường thẳng song song thay vì hai đường.
 Video Giải bài tập Toán lớp 8 hay, chi tiết
Video Giải bài tập Toán lớp 8 hay, chi tiết
Trả lời câu hỏi Toán 8 Tập 1 Bài 10 trang 102
Cho hình 96b với các đường thẳng a, b, c, d song song với nhau. Ta cần chứng minh:
a) Nếu các đường thẳng a, b, c, d song song cách đều thì EF = FG = GH.
b) Nếu EF = FG = GH thì các đường thẳng a, b, c, d song song cách đều.
Ở đây, các đường thẳng a, b, c, d cắt hai đường thẳng khác tạo ra các đoạn thẳng AE, EF, FG, GH trên một đường thẳng và AB, BC, CD trên đường thẳng còn lại. E, F, G, H nằm trên một đường thẳng, còn A, B, C, D (và các điểm tương ứng) nằm trên một đường thẳng khác.
Phân tích:
Đây là bài toán áp dụng trực tiếp định lý về đường thẳng song song cách đều.
Phần a) Chứng minh:
Giả sử các đường thẳnga, b, c, dsong song cách đều. Điều này có nghĩa là khoảng cách giữaavàbbằng khoảng cách giữabvàc, bằng khoảng cách giữacvàd.
Theo định lý về đường thẳng song song cách đều, nếu các đường thẳng song song cắt hai đường thẳng khác thì chúng định ra trên hai đường thẳng đó các đoạn thẳng tương ứng bằng nhau.
Ở đây, các đường thẳnga, b, c, dcắt hai đường thẳng định ra các đoạnAB, BC, CDtrên một đường thẳng vàEF, FG, GHtrên đường thẳng còn lại.
Vì các đường thẳng song song cách đều, nênAB = BC = CDvà suy raEF = FG = GH.Phần b) Chứng minh:
Giả sửEF = FG = GH. Ta cần chứng minh các đường thẳnga, b, c, dsong song cách đều.
Đây là mệnh đề đảo của định lý. Nếu các đường thẳng song song định ra trên hai đường thẳng cắt chúng các đoạn thẳng tương ứng bằng nhau thì chúng song song cách đều.
Trong trường hợp này, chúng định raAB = BC = CDvàEF = FG = GH.
Do đó, các đường thẳnga, b, c, dsong song cách đều.
Lời giải chi tiết (theo bài gốc):
a) “Các đường thẳng a, b, c, d song song cách đều ⇒ AB = BC = CD ⇒ B là trung điểm của AC; C là trung điểm của BD” (Phần này là suy luận đúng).
“- Hình thang AEGC (AE // GC) có B là trung điểm của AC và BF song song hai cạnh đáy ⇒ F là trung điểm EG (định lí đường trung bình của hình thang) ⇒ EF = FG” (Phần này áp dụng định lý đường trung bình của hình thang, tuy nhiên cách gọi tên hình thang và các đoạn thẳng cần xem lại hình vẽ gốc h.96b để chính xác hơn. Nhưng ý tưởng là đúng).
“- Chứng minh tương tự ⇒ G là trung điểm FH ⇒ FG = GH”
“Vậy EF = FG = GH”
b) Phần này chỉ cần nêu định lý đảo: Nếu các đường thẳng song song định ra các đoạn thẳng tương ứng bằng nhau trên hai đường thẳng cắt chúng thì chúng song song cách đều.
Mẹo kiểm tra:
Định lý đường thẳng song song cách đều là một định lý quan trọng. Hãy ghi nhớ nó.
Khi gặp bài toán về các đường thẳng song song cắt các đường thẳng khác, hãy nghĩ đến việc áp dụng định lý này.
Lỗi hay gặp:
Nhầm lẫn các đoạn thẳng tương ứng, hoặc không nhớ định lý đường trung bình của hình thang hoặc định lý về đường thẳng song song cách đều.
 Video Giải bài tập Toán lớp 8 hay, chi tiết
Video Giải bài tập Toán lớp 8 hay, chi tiết
Bài 67 trang 102 SGK Toán 8 Tập 1
Đề bài: Cho đoạn thẳng AB. Kẻ tia Ax bất kì. Trên tia Ax lấy các điểm C, D, E sao cho AC = CD = DE. Kẻ đoạn thẳng EB. Qua C, D kẻ các đường thẳng song song với EB. Chứng minh rằng đoạn thẳng AB bị chia ra ba phần bằng nhau.
Phân tích:
Chúng ta có các điểm C, D, E trên tia Ax thỏa mãn AC = CD = DE.
Có đoạn thẳng EB.
Qua C và D, ta kẻ các đường thẳng song song với EB. Gọi giao điểm của đường thẳng qua C với AB là P, và giao điểm của đường thẳng qua D với AB là Q. Yêu cầu chứng minh AP = PQ = QB.
Đây là bài toán áp dụng định lý về đường thẳng song song cách đều.
Lời giải:
Kẻ đường thẳng At song song với EB. Đường thẳng này sẽ đi qua A (nếu coi Ax là một đường thẳng và AB là một đường thẳng khác).
Tuy nhiên, cách diễn đạt của bài gốc như sau:
“Kẻ đường thẳng At // CC’ // DD’ // BE như hình vẽ.”
Ở đây, At không phải là tia Ax mà là một đường thẳng song song. CC' và DD' là các đường thẳng kẻ qua C và D song song với EB.
Quan trọng là các đường thẳng này: At, CC', DD', EB là song song với nhau.
Chúng cắt đường thẳng Ax tại các điểm A, C, D, E (với AC = CD = DE).
Chúng cắt đường thẳng AB tại các điểm mà ta gọi là P (giao điểm của CC' với AB) và Q (giao điểm của DD' với AB).
Theo định lý về đường thẳng song song cách đều: Nếu các đường thẳng song song cắt hai đường thẳng khác thì chúng định ra trên hai đường thẳng đó các đoạn thẳng tương ứng bằng nhau.
Ở đây, các đường thẳng song song At, CC', DD', EB định ra trên tia Ax các đoạn thẳng AC, CD, DE với AC = CD = DE.
Do đó, chúng cũng định ra trên đường thẳng AB các đoạn thẳng tương ứng bằng nhau. Gọi các giao điểm này là P và Q (với P là giao điểm của CC' với AB, Q là giao điểm của DD' với AB).
Khi đó, ta có AP = PQ = QB. Điều này có nghĩa là đoạn thẳng AB bị chia thành ba phần bằng nhau.
Mẹo kiểm tra:
Bài này là một ví dụ kinh điển của định lý đường thẳng song song cách đều. Hãy vẽ hình ra để hình dung rõ hơn.
Lỗi hay gặp:
Không vẽ hình hoặc vẽ hình không chính xác, dẫn đến việc áp dụng sai định lý.
 Giải bài 67 trang 102 Toán 8 Tập 1 | Giải bài tập Toán 8
Giải bài 67 trang 102 Toán 8 Tập 1 | Giải bài tập Toán 8 Giải bài 67 trang 102 Toán 8 Tập 1 | Giải bài tập Toán 8
Giải bài 67 trang 102 Toán 8 Tập 1 | Giải bài tập Toán 8
Bài 68 trang 102 SGK Toán 8 Tập 1
Đề bài: Cho điểm A nằm ngoài đường thẳng d và có khoảng cách đến d bằng 2cm. Lấy điểm B bất kì thuộc đường thẳng d. Gọi C là điểm đối xứng với điểm A qua điểm B. Khi điểm B di chuyển trên đường thẳng d, điểm C di chuyển trên đường nào?
Phân tích:
Alà điểm cố định,dlà đường thẳng cố định. Khoảng cách từAđếndlà2 cm.Blà điểm di động trênd.Clà điểm đối xứng vớiAquaB. Điều này có nghĩa làBlà trung điểm của đoạn thẳngAC.- Ta cần tìm quỹ tích của điểm
CkhiBdi chuyển trênd.
Vì B là trung điểm của AC, nên A, B, C thẳng hàng và AB = BC.
Do B thuộc đường thẳng d, nên A, B, C thẳng hàng và BC = AB.
Khi B di chuyển trên d, điểm C sẽ di chuyển sao cho BC bằng đúng độ dài đoạn AB.
Gọi H là hình chiếu của A trên d. Ta có AH = 2 cm và AH ⊥ d.
Xét tam giác AHB vuông tại H.
Xét tam giác CKB vuông tại K (với K là hình chiếu của C trên d).
Vì C đối xứng với A qua B, nên B là trung điểm của AC.
Xét hai tam giác vuông AHB và CKB.
Ta có:
AB = BC(theo định nghĩa điểm đối xứng).- Góc
ABHvà gócCBKlà hai góc đối đỉnh, nên bằng nhau. Tuy nhiên,AHBvàCKBlà hai tam giác vuông.
Ta cần sử dụng tính chất đối xứng qua một điểm. KhiCđối xứng vớiAquaB, thìA, B, Cthẳng hàng vàAB = BC.
VìBthuộc đường thẳngd, vàAH ⊥ d, ta có thể sử dụng phép đối xứng tâmB. Phép đối xứng tâmBbiếnAthànhC.
Nếu ta hạ đường vuông góc từAxuốngdtạiH, thì ảnh củaHqua phép đối xứng tâmB(tức là điểmKsao choBlà trung điểmHK) sẽ nằm trên đường thẳngd. Tuy nhiên,Ckhông nhất thiết phải tạo thành tam giác vuôngCKBvớiKlà hình chiếu củaC.
Hãy xem lại mối liên hệ giữa AH và khoảng cách từ C đến d.
Khi B di chuyển trên d, AB thay đổi độ dài.
Nhưng C đối xứng với A qua B nghĩa là B là trung điểm AC.
Ta có thể sử dụng vector hoặc tọa độ để giải bài này, nhưng theo cách cấp 2, ta sẽ dùng hình học.
Xét phép đối xứng qua điểm B. Điểm A biến thành C.
Đường thẳng d chứa B.
Nếu ta có một đường thẳng d’ song song với d, thì phép đối xứng tâm B sẽ biến đường thẳng d thành chính nó (nếu B nằm trên d).
Tuy nhiên, điểm C có mối quan hệ gì với khoảng cách 2cm?
Xét hình chiếu của A lên d là H, AH = 2cm.
Khi B di chuyển trên d, ta có thể xem B là gốc tọa độ trên đường thẳng d. Điểm A có tọa độ (x_A, y_A). Đường thẳng d có phương trình y=0. Khoảng cách y_A = 2 (nếu chọn H là gốc và AH là trục y).
Nếu A có tọa độ (0, 2) và d là trục x (y=0). Điểm B là (x_B, 0).
Điểm C đối xứng với A qua B. B là trung điểm AC.x_B = (0 + x_C) / 2 => x_C = 2x_B.0 = (2 + y_C) / 2 => y_C = -2.
Vậy, tọa độ điểm C là (2x_B, -2). Vì x_B có thể là bất kỳ số thực nào, 2x_B cũng có thể là bất kỳ số thực nào. Do đó, điểm C có tọa độ (X, -2) với X là số thực bất kỳ.
Điều này có nghĩa là C di chuyển trên đường thẳng y = -2.
Đường thẳng y = -2 là đường thẳng song song với đường thẳng d (trục x, y=0) và cách d một khoảng |-2| = 2 cm.
Kết quả:
Điểm C di chuyển trên một đường thẳng song song với d và cách d một khoảng bằng 2 cm. Cụ thể, nó nằm ở phía đối diện với A so với đường thẳng d.
Lời giải lại:
Gọi H là hình chiếu của A trên đường thẳng d. Theo giả thiết, AH = 2 cm và AH ⊥ d.
Gọi K là hình chiếu của C trên đường thẳng d.
Vì C đối xứng với A qua điểm B trên đường thẳng d, nên B là trung điểm của đoạn thẳng AC.
Xét tam giác AHB và tam giác CKB.
Ta có: AB = BC (do B là trung điểm AC).
Góc AHB = Góc CKB = 90^circ.
Góc ABH và góc CBK không nhất thiết bằng nhau trừ khi AB ⊥ d.
Hãy sử dụng định lý về sự đối xứng:
Phép đối xứng tâm B biến A thành C.
Do B nằm trên đường thẳng d, phép đối xứng tâm B biến đường thẳng d thành chính nó.
Tuy nhiên, điều này không giúp ta tìm quỹ tích C.
Ta có AH ⊥ d. Gọi đường thẳng qua A song song với d là d_A. Khoảng cách từ A đến d là 2cm.
Khi B di chuyển trên d, C là điểm sao cho B là trung điểm AC.
Ta có thể chứng minh CK = AH = 2cm và CK // AH.
Xét đường thẳng d. Gọi H là hình chiếu của A trên d, AH = 2cm.
Khi B di chuyển trên d, C là ảnh của A qua phép đối xứng tâm B.
Ta cần chứng minh rằng khoảng cách từ C đến d là 2cm và C nằm trên một đường thẳng.
Xét đường thẳng qua A song song với d. Gọi d' là đường thẳng qua A song song với d. Khoảng cách giữa d và d' là 2cm.
Điểm C đối xứng với A qua B (B trên d).
Điều này tương đương với vector BC = BA, hay C = B + (B - A) = 2B - A.
Nếu ta đặt A = (x_A, y_A), d là trục x (y=0), thì y_A = 2 hoặc y_A = -2. Giả sử y_A = 2. A = (x_A, 2).B = (x_B, 0).C = 2(x_B, 0) - (x_A, 2) = (2x_B - x_A, -2).
Vậy y_C = -2. Điểm C luôn có tung độ là -2.
Đường thẳng d có phương trình y=0.
Đường thẳng mà C di chuyển có phương trình y=-2.
Đây là đường thẳng song song với d và cách d một khoảng |-2| = 2cm.
Lời giải theo bài gốc:
Gọi H và K lần lượt là hình chiếu của A và C trên đường thẳng d.AH là khoảng cách từ A đến d, nên AH = 2cm.
Vì C đối xứng với A qua B, B là trung điểm của AC.
Xét tam giác AHB vuông tại H và tam giác CKB vuông tại K.
Ta có AB = BC.
Nếu AH và CK cùng vuông góc với d, và B nằm trên d, thì AH // CK.
Xét hai tam giác AHB và CKB. Ta có:AB = BC (cạnh huyền)
Góc ABH = Góc CBK (đối đỉnh).
Nếu AH và CK cùng vuông góc với d, thì chúng song song với nhau.
Xét hai tam giác AHB và CKB có:AB = BC (cạnh huyền)AH = CK (cần chứng minh)
Góc AHB = Góc CKB = 90^circ.
Nếu ta chứng minh được AH // CK, thì hai tam giác này sẽ bằng nhau theo trường hợp cạnh huyền – cạnh góc vuông.
Vì AH ⊥ d và CK ⊥ d, nên AH // CK.
Do đó, ΔAHB = ΔCKB (cạnh huyền – góc nhọn, góc ABH không nhất thiết bằng CBK).
Phải dùng định lý 2 tam giác bằng nhau: cạnh huyền – cạnh góc nhọn.
Xét ΔAHB và ΔCKB.AB = BC (gt)AH = CK (cần chứng minh).
Góc AHB = Góc CKB = 90^circ.
Suy ra ΔAHB và ΔCKB bằng nhau theo trường hợp cạnh huyền – cạnh góc vuông nếu AH = CK.
Chứng minh AH = CK:
Vì B là trung điểm AC, và AH // CK (cùng vuông góc với d), ta có thể chứng minh AH = CK.
Xét hình thang AHKC (với H, K trên d). Nếu AK và HK là các đường thẳng cắt nhau, và B là trung điểm AC, ta có thể suy ra mối liên hệ.
Cách đơn giản hơn:B là trung điểm AC. Tức là vec{B} = (vec{A} + vec{C})/2. Suy ra vec{C} = 2 vec{B} - vec{A}.
Nếu ta đặt đường thẳng d là trục hoành y=0. Điểm A có tọa độ (x_A, 2).
Điểm B có tọa độ (x_B, 0).
Điểm C sẽ có tọa độ (2x_B - x_A, -2).
Hoành độ của C có thể thay đổi tùy theo x_B, còn tung độ luôn là -2.
Vậy C di chuyển trên đường thẳng y = -2.
Đường thẳng này song song với d (trục hoành y=0) và cách d một khoảng 2cm.
Kết quả:
Điểm C nằm trên đường thẳng song song với d và cách d một khoảng 2cm.
Lời giải bài gốc diễn giải:
“Gọi H, K là hình chiếu của A và C trên đường thẳng d. ⇒ Khoảng cách từ A đến d bằng AH ⇒ AH = 2cm.
Xét ΔAHB vuông tại H và ΔCKB vuông tại K có:
AB = BC
⇒ ΔAHB = ΔCKB (cạnh huyền – góc nhọn)”
Phần này cần chứng minh thêm AH = CK hoặc AH // CK để suy ra tam giác bằng nhau. AH // CK là đúng vì cả hai đều vuông góc với d. Nếu AH và CK là hai đoạn thẳng tương ứng của hai tam giác vuông bằng nhau thì chúng phải bằng nhau.
“⇒ CK = AH = 2cm.
Vậy điểm C nằm trên đường thẳng song song với d, không đi qua A và cách d 2cm.” (Phần “không đi qua A” là không cần thiết, điểm C có thể nằm trên đường thẳng này).
 Giải bài 68 trang 102 Toán 8 Tập 1 | Giải bài tập Toán 8
Giải bài 68 trang 102 Toán 8 Tập 1 | Giải bài tập Toán 8
Bài 69 trang 103 SGK Toán 8 Tập 1
Đề bài: Ghép mỗi ý (1), (2), (3), (4) với một trong các ý (5), (6), (7), (8) để được một khẳng định đúng.
Phân tích:
Đây là bài tập ôn tập về các tập hợp điểm đặc biệt, liên quan đến khoảng cách và tính chất đối xứng, cũng như đường thẳng song song.
(1) Tập hợp các điểm cách A cố định một khoảng 3cm:
Điểm cố địnhAđóng vai trò là tâm. Khoảng cách không đổi3cmlà bán kính. Tập hợp các điểm này tạo thành một đường tròn.
Ghép với (7) là đường tròn tâm A bán kính 3cm.(2) Tập hợp các điểm cách đều hai đầu của đoạn thẳng AB cố định:
Đây là định nghĩa của đường trung trực của đoạn thẳngAB.
Ghép với (5) Là đường trung trực của đoạn thẳng AB.(3) Tập hợp các điểm nằm trong góc xOy và cách đều hai cạnh của góc đó:
Đây là định nghĩa của tia phân giác của gócxOy.
Ghép với (8) là tia phân giác của góc xOy.(4) Tập hợp các điểm cách đều đường thẳng a cố định một khoảng 3cm:
Tương tự như bài tập trước, tập hợp các điểm cách một đường thẳng cố định một khoảng không đổi là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng khoảng cách đã cho.
Ghép với (6) là hai đường thẳng song song với a và cách a một khoảng 3cm.
Lời giải:
Ghép các ý theo phân tích:
(1) với (7)
(2) với (5)
(3) với (8)
(4) với (6)
| (1) Tập hợp các điểm cách A cố định một khoảng 3cm. (2) Tập hợp các điểm cách đều hai đầu của đoạn thẳng AB cố định (3) Tập hợp các điểm nằm trong góc xOy và cách đều hai cạnh của góc đó (4) Tập hợp các điểm cách đều đường thẳng a cố định một khoảng 3cm. | (5) Là đường trung trực của đoạn thẳng AB. (6) là hai đường thẳng song song với a và cách a một khoảng 3cm. (7) là đường tròn tâm A bán kính 3cm. (8) là tia phân giác của góc xOy |
|---|---|
| (1) → (7) | (5) ← (2) |
| (2) → (5) | (6) ← (4) |
| (3) → (8) | (7) ← (1) |
| (4) → (6) | (8) ← (3) |
Đáp Án/Kết Quả
Tóm tắt lại các kết quả chính từ các bài tập:
- Bài 1 (Trang 100): Nếu hai đường thẳng song song, các đoạn vuông góc kẻ từ hai điểm bất kỳ trên đường này xuống đường kia có độ dài bằng nhau. BK = AH = h.
- Bài 2 (Trang 101): Điểm cách đều đường thẳng
bmột khoảnghvà nằm trên nửa mặt phẳng xác định sẽ thuộc đường thẳnga(hoặca’) song song vớibvà cáchbmột khoảngh. - Bài 3 (Trang 101): Tập hợp các đỉnh
Acủa tam giácABCvớiBCcố định và đường cao ứng vớiBCbằng2cmlà một đường thẳng song song vớiBCvà cáchBCmột khoảng2cm. - Bài 4 (Trang 102): Nếu các đường thẳng song song cách đều, chúng định ra trên hai đường thẳng cắt chúng các đoạn thẳng tương ứng bằng nhau. Ngược lại, nếu chúng định ra các đoạn thẳng tương ứng bằng nhau thì chúng song song cách đều.
- Bài 67 (Trang 102): Đoạn thẳng
ABbị chia ba phần bằng nhau bởi các đường thẳng song song vớiEBkẻ qua các điểm chia đoạnAxthành ba phần bằng nhau (AC = CD = DE). - Bài 68 (Trang 102): Điểm
Cđối xứng vớiAqua điểmBtrên đường thẳngdsẽ di chuyển trên một đường thẳng song song vớidvà cáchdmột khoảng bằng khoảng cách từAđếnd(2cm). - Bài 69 (Trang 103): Ôn tập các tập hợp điểm quan trọng: đường tròn, đường trung trực, tia phân giác, hai đường thẳng song song cách đều.
Kết Luận
Qua bài 10 về đường thẳng song song, các em đã được củng cố và mở rộng kiến thức về các tính chất quan trọng của đường thẳng song song, định lý đường trung bình của hình thang và định lý đường thẳng song song cách đều. Việc hiểu rõ các khái niệm này không chỉ giúp các em giải quyết tốt các bài tập trong sách giáo khoa mà còn là nền tảng vững chắc cho việc học các kiến thức hình học nâng cao hơn. Hãy luyện tập thường xuyên để nắm vững chủ đề giải toán lớp 8 bài 10 này.
Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.