Giải Toán Phần Trăm Lớp 5: Lý Thuyết Và Bài Tập Chi Tiết

by Thầy Đông · January 7, 2026

Rate this post

Nắm vững giải toán phần trăm lớp 5 là chìa khóa giúp học sinh tiểu học tự tin chinh phục các bài toán liên quan đến tỉ lệ và số liệu. Bài viết này cung cấp lý thuyết đầy đủ, các dạng bài tập phổ biến cùng phương pháp giải chi tiết, giúp các em học sinh và phụ huynh hiểu sâu về chủ đề quan trọng này.

Đề Bài

Hiện tại, bài viết tập trung vào lý thuyết và các dạng toán chung về tỉ số phần trăm lớp 5, chưa có một đề bài cụ thể được đưa ra để giải. Nội dung dưới đây sẽ trình bày tổng quan về khái niệm, công thức và các dạng toán thường gặp.

Phân Tích Yêu Cầu

Bài viết này có mục tiêu cung cấp kiến thức nền tảng và kỹ năng giải quyết các bài toán về tỉ số phần trăm dành cho học sinh lớp 5. Yêu cầu cốt lõi là làm rõ:

Khái niệm tỉ số phần trăm: Tỉ số phần trăm là gì và cách biểu diễn chúng.
Các phép tính với tỉ số phần trăm: Cộng, trừ, nhân, chia tỉ số phần trăm.
Các dạng toán trọng tâm: Bao gồm tìm tỉ số phần trăm của hai số, tìm giá trị phần trăm của một số, tìm một số khi biết giá trị phần trăm của nó, bài toán về lãi suất và các bài toán nâng cao hơn.
Phương pháp giải chi tiết: Hướng dẫn từng bước để giải quyết từng dạng bài tập.

Mục tiêu cuối cùng là giúp học sinh có thể áp dụng linh hoạt các kiến thức này vào bài tập thực tế và kỳ thi.

Kiến Thức/Nền Tảng Cần Dùng

Để tiếp cận chủ đề giải toán phần trăm lớp 5, học sinh cần nắm vững các kiến thức cơ bản sau:

Khái niệm Tỉ số phần trăm

Tỉ số phần trăm là một cách biểu diễn tỉ số của hai số dưới dạng phần trăm, tức là quy mẫu số của tỉ số về 100. Ký hiệu phần trăm là %.

Một phân số có mẫu số là 100 có thể được viết dưới dạng phần trăm. Ví dụ:
- 1/100 được viết là 1%.
- 15/100 được viết là 15%.
- Tổng quát, a/100 được viết là a%.

Việc hiểu rõ khái niệm này giúp học sinh dễ dàng quy đổi giữa phân số, số thập phân và tỉ số phần trăm.

Các Phép tính với Tỉ số phần trăm

Các phép tính với tỉ số phần trăm về cơ bản được thực hiện tương tự như các phép tính với số tự nhiên hoặc số thập phân, sau đó kết quả sẽ được thêm ký hiệu %.

Phép cộng:
a% + b% = (a + b)%
Ví dụ: 20% + 8% = (20 + 8)% = 28%
Phép trừ:
a% - b% = (a - b)%
Ví dụ: 68% - 32% = (68 - 32)% = 36%
Phép nhân tỉ số phần trăm với một số:
a% times b = (a times b)%
Ví dụ: 14% times 4 = (14 times 4)% = 56%
Phép chia tỉ số phần trăm cho một số:
a% : b = (a : b)%
Ví dụ: 48% : 4 = (48 : 4)% = 12%

Những quy tắc này là nền tảng để thực hiện các phép tính trong nhiều dạng toán.

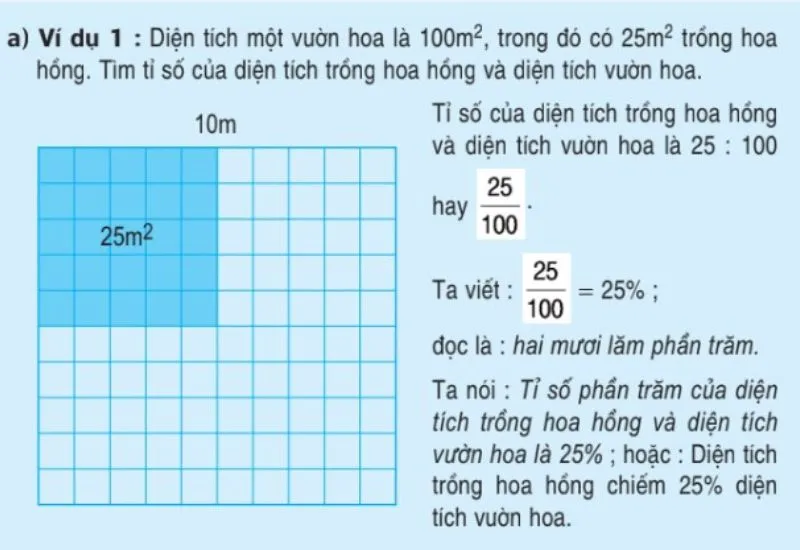Hình 1: Minh họa khái niệm tỉ số phần trăm trong toán lớp 5.
Hình 2: Các ví dụ về tỉ số phần trăm từ sách giáo khoa.

Hướng Dẫn Giải Chi Tiết

Chúng ta sẽ đi vào chi tiết các dạng toán thường gặp về tỉ số phần trăm lớp 5.

Dạng 1: Bài toán về cộng, trừ, nhân, chia tỉ số phần trăm

Đây là dạng toán cơ bản nhất, yêu cầu áp dụng trực tiếp các quy tắc phép tính đã nêu ở phần kiến thức nền tảng.

Phương pháp giải:

Thực hiện các phép tính cộng, trừ, nhân, chia như thông thường với các con số, sau đó ghi thêm ký hiệu phần trăm (%) vào kết quả cuối cùng.

Ví dụ: Tính:
a) 20% + 8%
b) 68% - 32%
c) 14% times 4
d) 48% : 4

Bài làm:
a) 20% + 8% = (20 + 8)% = 28%
b) 68% - 32% = (68 - 32)% = 36%
c) 14% times 4 = (14 times 4)% = 56%
d) 48% : 4 = (48 : 4)% = 12%

Mẹo kiểm tra: Đối với phép cộng, trừ, kết quả phải nằm trong khoảng hợp lý với các số hạng. Với phép nhân, kết quả sẽ lớn hơn số ban đầu (khi nhân với số lớn hơn 1). Với phép chia, kết quả sẽ nhỏ hơn số ban đầu (khi chia cho số lớn hơn 1).

Lỗi hay gặp: Quên ghi ký hiệu phần trăm (%) vào kết quả cuối cùng.

Hình 3: Minh họa các phép tính về tỉ số phần trăm.

Dạng 2: Tìm tỉ số phần trăm của hai số

Dạng toán này yêu cầu tìm xem một số bằng bao nhiêu phần trăm so với một số khác.

Công thức:

Để tìm tỉ số phần trăm của số A so với số B, ta thực hiện phép chia A cho B rồi nhân với 100, hoặc lấy A chia B để được tỉ số dưới dạng số thập phân, sau đó nhân với 100.

Tỉ số phần trăm = (Số A : Số B) times 100%

Hoặc có thể hiểu là:
Tỉ số phần trăm = (Số A / Số B) times 100 (sau đó thêm dấu % vào kết quả)

Trong đó:

A là số được nhắc trước (thường là một phần của tổng thể).
B là số được nhắc sau (thường là tổng thể).
Kết quả là tỉ lệ dưới dạng phần trăm.

Ví dụ: Khối lớp 4 của một trường tiểu học có 200 học sinh, trong đó có 80 học sinh nam.
a) Tính tỉ số phần trăm của số học sinh nữ với số học sinh khối 4.
b) Tính tỉ số phần trăm của số học sinh nam với số học sinh khối 4.

Bài làm:

Bước 1: Tìm số học sinh nữ.
Số học sinh nữ của khối lớp 4 là: 200 - 80 = 120 (học sinh)
Bước 2: Tính tỉ số phần trăm theo yêu cầu.
a) Tỉ số phần trăm của số học sinh nữ với số học sinh khối lớp 4 là:
120 : 200 times 100 = 0,6 times 100 = 60%
b) Tỉ số phần trăm của số học sinh nam với số học sinh khối lớp 4 là:
80 : 200 times 100 = 0,4 times 100 = 40%

Đáp số:
a) 60%
b) 40%

Mẹo kiểm tra: Tổng tỉ số phần trăm của các bộ phận so với tổng thể phải bằng 100%. Ở ví dụ trên, 60% + 40% = 100%, đúng với tổng số học sinh toàn khối.

Lỗi hay gặp: Đảo ngược số A và số B trong công thức, dẫn đến kết quả sai. Cần đọc kỹ đề để xác định số nào là “phần” và số nào là “toàn thể”.

Dạng 3: Tìm giá trị phần trăm của một số

Dạng toán này cho biết một số và tỉ lệ phần trăm mà nó chiếm trong một tổng thể, yêu cầu tìm giá trị cụ thể của phần đó.

Công thức:

Muốn tìm giá trị phần trăm của một số, ta lấy số đó nhân với số phần trăm đã cho rồi chia cho 100.

Giá trị cần tìm = Số ban đầu times Số phần trăm / 100

Hoặc có thể hiểu là:
Giá trị cần tìm = Số ban đầu times (Số phần trăm / 100)

Ví dụ: Lớp 5A có 50 học sinh, trong đó số học sinh nữ chiếm 60%. Hỏi số học sinh nữ của lớp là bao nhiêu học sinh?

Bài làm:

Bước 1: Xác định “số ban đầu” và “số phần trăm”.
Số ban đầu (tổng số học sinh) là 50.
Số phần trăm (tỉ lệ học sinh nữ) là 60%.
Bước 2: Áp dụng công thức.
Số học sinh nữ của lớp 5A là:
50 times 60 / 100 = 3000 / 100 = 30 (học sinh)

Đáp số: 30 học sinh.

Hình 4: Cách tính dạng toán tìm giá trị phần trăm của một số.

Mẹo kiểm tra: Giá trị phần trăm tìm được phải nhỏ hơn hoặc bằng số ban đầu. Nếu số phần trăm là 100%, thì giá trị tìm được bằng số ban đầu. Nếu số phần trăm nhỏ hơn 100%, giá trị tìm được sẽ nhỏ hơn.

Lỗi hay gặp: Nhầm lẫn giữa dạng toán này với dạng “tìm tỉ số phần trăm của hai số” hoặc “tìm một số khi biết giá trị phần trăm”.

Dạng 4: Tìm một số khi biết giá trị phần trăm của số đó

Dạng toán này cho biết một phần của tổng thể (giá trị cụ thể) và tỉ lệ phần trăm mà phần đó chiếm, yêu cầu tìm giá trị của toàn thể.

Công thức:

Lấy giá trị đã biết chia cho số phần trăm tương ứng rồi nhân với 100.

Số cần tìm = Giá trị đã biết / Số phần trăm times 100

Hoặc có thể hiểu là:
Số cần tìm = Giá trị đã biết / (Số phần trăm / 100)

Ví dụ: Một chai sữa có 4,5% bơ, biết rằng trọng lượng của bơ trong chai sữa là 18g. Tính lượng sữa trong một chai.

Bài làm:

Bước 1: Xác định “giá trị đã biết” và “số phần trăm”.
Giá trị đã biết (trọng lượng bơ) là 18g.
Số phần trăm (tỉ lệ bơ) là 4,5%.
Bước 2: Áp dụng công thức.
Lượng sữa có trong chai là:
18 / 4,5 times 100 = 4 times 100 = 400 (g)

Đáp số: 400g.

Mẹo kiểm tra: Số cần tìm phải lớn hơn giá trị đã biết. Nếu số phần trăm càng nhỏ, thì số cần tìm (tổng thể) càng lớn.

Lỗi hay gặp: Nhầm lẫn công thức với dạng toán “tìm giá trị phần trăm của một số”.

Dạng 5: Bài toán về tính lãi, tính vốn

Dạng bài này thường áp dụng trong các tình huống mua bán thực tế, liên quan đến giá vốn, giá bán, lãi và lỗ.

Các công thức cơ bản:

Giá bán = Giá vốn + Tiền lãi
Giá vốn = Giá bán – Tiền lãi
Tiền lãi = Giá bán – Giá vốn
Giá bán = Giá vốn – Tiền lỗ (Lỗ được hiểu là lãi âm)

Khi bài toán cho tỉ lệ phần trăm lãi hoặc lỗ, ta quy tỉ lệ đó ra giá trị thực tế dựa trên giá vốn hoặc giá bán đã cho.

Ví dụ 1: Một chiếc xe đạp giá 2.000.000 đồng, nay giảm giá 20%. Hỏi giá chiếc xe đạp này bây giờ có giá là bao nhiêu?

Bài làm:

Bước 1: Coi giá ban đầu là 100%. Tính tỉ lệ phần trăm sau khi giảm giá.
Sau khi giảm giá 20%, giá xe đạp còn lại là:
100% - 20% = 80% (so với giá ban đầu)
Bước 2: Tính giá trị thực tế sau khi giảm giá.
Giá của chiếc xe đạp hiện nay là:
2.000.000 times 80 / 100 = 1.600.000 (đồng)

Đáp số: 1.600.000 đồng.

Hình 5: Cách tính dạng toán tỉ số phần trăm trong kinh doanh.

Mẹo kiểm tra: Nếu giảm giá, giá mới phải nhỏ hơn giá ban đầu. Nếu tăng giá, giá mới phải lớn hơn giá ban đầu.

Lỗi hay gặp: Nhầm lẫn tỉ lệ phần trăm áp dụng trên giá nào (giá vốn hay giá bán). Đọc kỹ đề để xác định đúng.

Dạng 6: Bài toán đưa về dạng toán quen thuộc

Một số bài toán có cấu trúc phức tạp hơn, đòi hỏi học sinh phải phân tích, biến đổi hoặc đưa về một trong các dạng toán cơ bản đã nêu ở trên để giải quyết.

Ví dụ: Tổng của hai số bằng 25% thương của hai số đó cũng bằng 25%. Tìm hai số đó.

Phân tích đề bài: Đề bài có vẻ hơi khó hiểu ban đầu. Chúng ta cần diễn giải lại:

Có hai số, gọi là A và B.
Tổng của hai số: A + B = ?
Thương của hai số: A / B = ? hoặc B / A = ? (cần xác định rõ hơn)
Đề cho: A + B = 25% (của cái gì đó?) và A / B = 25% (của cái gì đó?) hoặc có thể hiểu đề bài muốn nói: “Tổng hai số X và Y là A. Thương hai số đó là B. Tìm X và Y biết A=25% và B=25%.” – Cách diễn giải này cũng chưa rõ ràng.

Diễn giải lại đề bài dựa trên các bài toán tương tự và kết quả mẫu:
Giả sử đề bài có ý: “Tổng của hai số là A. Tỉ số của hai số đó là B. Tính hai số đó.” Hoặc có thể hiểu “Tổng của hai số là một giá trị X. Thương của hai số đó là một giá trị Y. Biết X = 25% và Y = 25% (của cái gì đó).”
Tuy nhiên, cách giải được đưa ra là 25% = 0,25, Số thứ nhất là: 0,25 : (1+4) = 0,05, Số thứ hai là: 0,25 – 0,05 = 0,2.
Cách giải này cho thấy:

0,25 có thể là tỉ số của hai số, ví dụ A/B = 0,25.
(1+4) có thể xuất phát từ tỉ lệ A:B = 1:4 hoặc A:B = 4:1.
0,25 - 0,05 = 0,2.

Dựa vào cách giải, có thể suy luận đề bài có ý như sau: “Hai số có tỉ số là 0,25. Tổng của hai số đó là một giá trị X (hoặc tỉ số của chúng là 0,25). Tìm hai số đó.”
Nếu A/B = 0,25 tức là A = 0,25B.
Nếu A+B = Y
Nếu A:B = 1:4 hoặc 4:1.
Cần làm rõ cách diễn giải đề gốc.

Diễn giải lại dựa trên quy tắc “Đưa về dạng toán quen thuộc” và cách giải được cung cấp:
Đề bài có thể ám chỉ: “Có hai số. Thương của hai số đó là 25% (tức là 0,25). Tổng của hai số đó… (phần này thiếu dữ liệu hoặc cách diễn đạt khác). Tuy nhiên, cách giải mẫu: 25% = 0,25, Số thứ nhất là: 0,25 : (1+4) = 0,05, Số thứ hai là: 0,25 – 0,05 = 0,2.
Điều này cho thấy tỉ số A/B = 0,25. Từ 0,25 và (1+4) thì có thể suy ra tỉ số giữa hai phần là 1:4 (hoặc 4:1) và tổng số phần là 1+4=5. Nếu 0,25 là một phần của tổng thì 0,25/5 = 0,05 (một phần) và 0,05 4 = 0,2 (bốn phần). Vậy bài toán có thể là: “Hai số có tỉ số là 0,25. Biết một phần nào đó (có thể là tổng các số, hoặc một số nào đó liên quan) bằng 0,25.”
Cách diễn giải này khá phức tạp do đề gốc chưa rõ ràng. Tuy nhiên, để minh họa cho dạng bài “đưa về dạng quen thuộc”, ta có thể giả định đề bài yêu cầu tìm hai số khi biết tỉ số của chúng và một thông tin liên quan khác.

Bài làm (dựa trên cách giải mẫu):

Bước 1: Quy đổi 25% về dạng số thập phân: 25% = 0,25.
Bước 2: Giả sử tỉ số của hai số là 0,25. Để áp dụng công thức tổng tỉ hoặc hiệu tỉ, chúng ta cần một mối liên hệ khác. Dựa vào phép chia 0,25 : (1+4), ta suy ra tỉ lệ là 1:4.
- Xem 0,25 là giá trị của một phần (hoặc tổng tỉ lệ gì đó).
- Tổng số phần là 1 + 4 = 5 phần.
Bước 3: Tìm giá trị của một phần.
Giá trị của một phần là: 0,25 : 5 = 0,05.
Bước 4: Tìm giá trị của từng số (tương ứng với số phần).
Số thứ nhất (với 1 phần) là: 0,05.
Số thứ hai (với 4 phần) là: 0,05 times 4 = 0,2.

Đáp số: Hai số đó là 0,05 và 0,2.

Mẹo kiểm tra: Kiểm tra xem tỉ số của hai số có đúng là 0,25 không và tổng của chúng có liên quan đến 0,25 theo đề bài hay không (tùy thuộc vào cách diễn giải chính xác của đề). 0,2 / 0,05 = 4, không phải 0,25. 0,05 / 0,2 = 0.25. Vậy tỉ số là 0,25. Tuy nhiên, mối liên hệ với “tổng của hai số” trong đề bài gốc lại không rõ ràng.

Lỗi hay gặp: Hiểu sai đề bài do cách diễn đạt chưa rõ ràng, dẫn đến áp dụng sai phương pháp.

Một số bài tập toán lớp 5 tỉ số phần trăm để các em luyện tập

Để củng cố kiến thức, học sinh nên luyện tập thường xuyên với các bài toán đa dạng. Dưới đây là một số bài tập tiêu biểu:

Bài 1: Một sản phẩm đã hạ giá bán 20%. Hỏi muốn bán sản phẩm đó với giá ban đầu thì phải tăng giá thêm bao nhiêu phần trăm?

Bài 2: Một tấm vải sau khi giặt xong bị co mất 2% chiều dài ban đầu. Giặt xong tấm vải chỉ còn 24,5m. Hỏi trước khi giặt tấm vải dài bao nhiêu mét?

Bài 3: Cô giáo đem chia táo cho học sinh. Nếu mỗi em 9 quả thì thiếu 9 quả. Nếu chia mỗi em 10 quả thì thiếu 25% số táo ban đầu. Tính số táo cô đem chia và số học sinh được chia táo.

Bài 4: Một nhà thầu xây dựng nhận xây cất một ngôi nhà với chi phí là 360.000.000 đồng nhưng chủ nhà xin hạ bớt 2,5%, nhà thầu đồng ý. Tính số tiền nhà thầu nhận xây nhà?

Bài 5: Nước biển chứa 4% muối. Cần đổ thêm bao nhiêu gam nước lã vào 400 gam nước biển để tỉ lệ muối trong dung dịch là 2%?

Bài 6: Một người đem trứng đi bán: buổi sáng bán được 50% số trứng, buổi chiều bán được 20% số trứng còn lại. Sau đó người đó lại buôn thêm 40 quả nữa. Tối về người đó lại thấy rằng số trứng đem về bằng 120% số trứng mang đi. Hỏi người ấy mang đi mấy quả trứng?

Bài 7: Một lớp có 25% học sinh giỏi, 55% học sinh khá còn lại là học sinh trung bình. Tính số học sinh của lớp đó biết số học sinh trung bình là 5 bạn?

Bài 8: Tính tuổi hai anh em biết 62,5% tuổi anh hơn 75% tuổi em là 2 tuổi và 50% tuổi anh hơn 37,5% tuổi em là 7 tuổi.

Bài 9: Lượng muối chứa trong nước biển là 5%. Cần phải đổ thêm vào 200kg nước biển bao nhiêu kg nước lã để được một loại dung dịch chứa 2% muối?

Bài 10: Lượng nước trong cỏ tươi là 55%, trong cỏ khô là 10%. Hỏi phơi 100 kg cỏ tươi ta được bao nhiêu ki lô gam cỏ khô?

Bài 11: Nhân ngày 26-3, một cửa hàng bán đồ lưu niệm bán hạ giá 10% so với ngày thường. Tuy vậy họ vẫn lãi 8% so với giá vốn. Hỏi ngày thường họ lãi bao nhiêu phần trăm so với giá vốn?

Bài 12: Trong trường có 68% số học sinh biết tiếng Nga, 5% biết cả tiếng Anh lẫn tiếng Nga. Số còn lại chỉ biết tiếng Anh. Hỏi có bao nhiêu phần trăm số học sinh trong trường biết tiếng Anh?

Bài 13: Một người bán lẻ mua một số hộp sữa bột với giá 24.000 đồng/hộp, khi thanh toán tiền chủ hàng đã giảm cho người mua hàng một số tiền bằng 12,5% giá tiền một hộp. Sau đó người ấy bán lại số tiền sữa trên với tiền lãi bằng 33 1/3% giá vốn sau khi đã giảm bớt 20% trên giá niêm yết. Hỏi giá niêm yết trên một hộp sữa là bao nhiêu đồng?

Bài 14: Một cửa hàng buôn bán hoa quả đặt hàng 4,5 tấn cam với giá 18.000 đồng một kilôgam. Tiền vận chuyển là 1.600.000 đồng. Giả sử 10% số cam bị hỏng trong quá trình vận chuyển và tất cả số cam đều bán được. Hãy tính xem mỗi kg cam cần bán với giá bao nhiêu để thu lãi 8%?

Bài 15: Bố mua 2 đôi giày cho Tiến nhưng đều bị nhỏ nên mẹ phải mang bán 2 đôi giày đó đi. Mỗi đôi giày đều bán với giá 300.000 đồng. Trong đó một đôi bán nhiều hơn giá mua 20%, đôi kia bán ít hơn giá mua 20%. Hỏi mẹ Tiến bán được lãi hay lỗ bao nhiêu tiền?

Trọn bộ ứng dụng học tập Monkey giúp trẻ phát triển tư duy và ngôn ngữ, hỗ trợ việc học tập Toán – Tiếng Việt – Tiếng Anh trên lớp dễ dàng hơn.[

Một số lưu ý giúp bé học toán lớp 5 tỉ số phần trăm tốt

Để học tốt chủ đề giải toán phần trăm lớp 5, các em cần lưu ý những điểm sau:

Nắm chắc kiến thức lý thuyết và cách tính: Hiểu rõ định nghĩa, công thức và các dạng toán cơ bản là bước đầu tiên và quan trọng nhất. Điều này giúp học sinh nhận diện bài toán nhanh chóng và lựa chọn phương pháp giải phù hợp.
Chăm chỉ rèn luyện: Thực hành giải nhiều bài tập từ cơ bản đến nâng cao là cách tốt nhất để củng cố kỹ năng. Mỗi bài tập giải được sẽ giúp ghi nhớ kiến thức sâu hơn và tăng sự tự tin khi đối mặt với các bài toán tương tự.
Kết hợp học ứng dụng: Sử dụng các ứng dụng học tập như Monkey Math có thể hỗ trợ hiệu quả. Ứng dụng này cung cấp bài giảng được thiết kế theo chương trình giáo dục mới, phân chia theo cấp độ từ dễ đến khó, giúp trẻ tiếp thu kiến thức một cách có hệ thống và thú vị. Việc học bằng tiếng Anh trên ứng dụng còn giúp phát triển thêm ngôn ngữ.

Hình 7: Ứng dụng Monkey Math giúp bé học tốt môn toán.

Việc kết hợp giữa việc học lý thuyết, luyện tập chăm chỉ và ứng dụng công nghệ sẽ giúp học sinh nắm vững kiến thức toán lớp 5 tỉ số phần trăm, tạo nền tảng vững chắc cho các cấp học tiếp theo.

Monkey Math – Ứng dụng dạy toán số 1 cho trẻ mầm non và tiểu học theo chương trình GDPT mới. Ba mẹ TẢI ỨNG DỤNG và ĐĂNG KÝ GÓI HỌC ngay hôm nay để con được tiếp cận với kiến thức sớm nhé![

Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.