Đề thi học sinh giỏi các môn - chuyên đề bồi dưỡng HSG miễn phí

Khảo Sát Sự Biến Thiên Và Vẽ Đồ Thị Hàm Số Bậc Ba Chuẩn Xác Nhất

by · January 7, 2026

Rate this post

Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc ba là một chủ đề quan trọng trong chương trình Giải tích 12, đòi hỏi sự hiểu biết sâu sắc về đạo hàm, giới hạn và các tính chất của hàm số. Việc nắm vững quy trình này không chỉ giúp giải quyết các bài toán trong sách giáo khoa mà còn là nền tảng vững chắc cho các kiến thức nâng cao. Bài viết này sẽ trình bày chi tiết các bước thực hiện, từ phân tích yêu cầu đến hoàn thiện đồ thị, kèm theo các mẹo và lưu ý quan trọng để bạn đọc có thể tự tin chinh phục dạng bài này.

Đề Bài

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số bậc ba sau:

a) (y = 2 + 3x – x^3);

b) (y = x^3 + 4x^2 + 4x);

c) (y = x^3 + x^2 + 9x);

d) (y = -2x^3 + 5)

Phân Tích Yêu Cầu

Yêu cầu của bài toán là thực hiện hai công việc chính: khảo sát sự biến thiên và vẽ đồ thị cho từng hàm số bậc ba được cho.

  • Khảo sát sự biến thiên: Giai đoạn này tập trung vào việc phân tích hành vi của hàm số trên toàn bộ tập xác định của nó. Chúng ta cần xác định hàm số đồng biến hay nghịch biến trên từng khoảng, tìm các điểm cực trị (cực đại, cực tiểu) nếu có, và khảo sát các giới hạn tại vô cực cũng như các điểm đặc biệt khác trên đồ thị như tiệm cận (mặc dù hàm bậc ba không có tiệm cận đứng hoặc ngang, nhưng việc xem xét giới hạn tại vô cực là bắt buộc). Kết quả của bước này sẽ được tổng hợp trong bảng biến thiên, một công cụ trực quan mô tả đầy đủ sự thay đổi của hàm số.
  • Vẽ đồ thị: Dựa trên thông tin thu thập được từ quá trình khảo sát sự biến thiên, chúng ta sẽ tiến hành vẽ đồ thị hàm số. Bước này bao gồm việc xác định các giao điểm của đồ thị với hai trục tọa độ (Ox và Oy), xác định các điểm cực trị đã tìm thấy, và sử dụng tính đối xứng của đồ thị hàm bậc ba (nếu có điểm uốn) để phác thảo đường cong chính xác và mượt mà nhất.

Hiểu rõ mục đích của từng công đoạn giúp chúng ta tiếp cận bài toán một cách có hệ thống và chính xác.

Kiến Thức Nền Tảng Cần Dùng

Để thực hiện khảo sát sự biến thiên và vẽ đồ thị hàm số bậc ba, chúng ta cần vận dụng các kiến thức cốt lõi từ Giải tích 12, chủ yếu xoay quanh đạo hàm và giới hạn.

1. Tập Xác Định

Đa số các hàm số đa thức, bao gồm cả hàm số bậc ba, có tập xác định là tập hợp số thực, ký hiệu là (D = mathbb{R}). Điều này có nghĩa là hàm số được định nghĩa cho mọi giá trị của (x).

2. Đạo Hàm và Sự Biến Thiên

Đạo hàm của hàm số bậc ba (y = ax^3 + bx^2 + cx + d) (với (a ne 0)) là một hàm số bậc hai: (y’ = 3ax^2 + 2bx + c).

  • Chiều biến thiên: Dấu của đạo hàm (y’) cho biết hàm số đồng biến hay nghịch biến.
    • Nếu (y’ > 0) trên một khoảng, hàm số đồng biến trên khoảng đó.
    • Nếu (y’ < 0) trên một khoảng, hàm số nghịch biến trên khoảng đó.
  • Tìm điểm cực trị:
    • Hàm số đạt cực trị (cực đại hoặc cực tiểu) tại các điểm (x_i) mà tại đó đạo hàm (y’) đổi dấu. Thông thường, các điểm này là nghiệm của phương trình (y’ = 0).
    • Nếu (y’) chỉ bằng 0 tại một điểm (x_0) nhưng không đổi dấu qua (x_0), thì (x_0) không phải là điểm cực trị.
    • Nếu phương trình (y’=0) có hai nghiệm phân biệt (x_1, x_2), thì hàm số sẽ có hai điểm cực trị. Nếu phương trình (y’=0) có nghiệm kép hoặc vô nghiệm, hàm số có thể không có cực trị hoặc có cực trị đặc biệt tùy trường hợp.

3. Giới Hạn và Tiệm Cận

Đối với hàm bậc ba, chúng ta khảo sát giới hạn của hàm số khi (x) tiến ra vô cực:

  • (mathop {lim }limits_{x to – infty } y)
  • (mathop {lim }limits_{x to + infty } y)

Kết quả của các giới hạn này cho ta biết xu hướng của đồ thị khi (x) tiến ra xa về hai phía âm và dương vô cực. Hàm bậc ba không có tiệm cận đứng hay tiệm cận ngang.

4. Bảng Biến Thiên

Bảng biến thiên là một công cụ tóm tắt hữu ích, thể hiện:

  • Các giá trị của (x).
  • Các điểm mà đạo hàm bằng 0 hoặc không xác định.
  • Dấu của đạo hàm (y’).
  • Chiều biến thiên của hàm số (mũi tên đi lên cho đồng biến, mũi tên đi xuống cho nghịch biến).
  • Các giá trị cực trị (nếu có).
  • Các giới hạn tại vô cực.

5. Đồ Thị Hàm Số

Để vẽ đồ thị, chúng ta cần:

  • Giao điểm với trục tung (Oy): Tìm bằng cách cho (x=0), tính (y). Điểm có tọa độ ((0, y(0))).

  • Giao điểm với trục hoành (Ox): Tìm bằng cách cho (y=0), giải phương trình (ax^3 + bx^2 + cx + d = 0). Phương trình bậc ba có thể có 1, 2 hoặc 3 nghiệm thực, tương ứng với số giao điểm với trục hoành.

  • Điểm uốn và tâm đối xứng: Đồ thị hàm bậc ba luôn có một điểm uốn. Điểm này là tâm đối xứng của đồ thị. Tìm điểm uốn bằng cách giải phương trình (y”=0), sau đó tính giá trị (y) tương ứng.

    • Ta có: (y” = 6ax + 2b).
    • Giải (y” = 0 Rightarrow x = -dfrac{2b}{6a} = -dfrac{b}{3a}).
    • Tìm (y) tương ứng tại (x = -dfrac{b}{3a}).

  • Các điểm đặc biệt khác: Nếu cần, ta có thể tính thêm tọa độ một vài điểm khác để đồ thị được chính xác hơn, đặc biệt là các điểm cực trị đã tìm được.

Quy Trình Chuẩn Hóa

  1. Bước 1: Tìm tập xác định (TXĐ).
  2. Bước 2: Tính đạo hàm (y’).
  3. Bước 3: Tìm các điểm dừng: Giải phương trình (y’ = 0).
  4. Bước 4: Xét dấu đạo hàm (y’) và lập bảng biến thiên.
  5. Bước 5: Tính giới hạn tại vô cực và các điểm đặc biệt.
  6. Bước 6: Tìm giao điểm với các trục tọa độ.
  7. Bước 7: Tìm điểm uốn (tâm đối xứng).
  8. Bước 8: Vẽ đồ thị dựa trên bảng biến thiên và các điểm tìm được.

Hướng Dẫn Giải Chi Tiết

Câu a) (y = 2 + 3x – x^3)

  1. TXĐ: (D = mathbb{R}).

  2. Sự biến thiên:

    • Đạo hàm: (y’ = 3 – 3x^2).
    • Các điểm dừng: (y’ = 0 Leftrightarrow 3 – 3x^2 = 0 Leftrightarrow x^2 = 1 Leftrightarrow x = 1) hoặc (x = -1).
    • Xét dấu (y’) và chiều biến thiên:
      • Trên khoảng (left( -infty, -1 right)), chọn (x=-2), (y’ = 3 – 3(-2)^2 = 3 – 12 = -9 < 0). Hàm số nghịch biến.
      • Trên khoảng (left( -1, 1 right)), chọn (x=0), (y’ = 3 – 3(0)^2 = 3 > 0). Hàm số đồng biến.
      • Trên khoảng (left( 1, +infty right)), chọn (x=2), (y’ = 3 – 3(2)^2 = 3 – 12 = -9 < 0). Hàm số nghịch biến.
    • Cực trị:
      • Tại (x = -1), (y’) đổi dấu từ (-rightarrow +). Hàm số đạt cực tiểu. (y_{CT} = y(-1) = 2 + 3(-1) – (-1)^3 = 2 – 3 + 1 = 0).
      • Tại (x = 1), (y’) đổi dấu từ (+rightarrow -). Hàm số đạt cực đại. (y_{CD} = y(1) = 2 + 3(1) – (1)^3 = 2 + 3 – 1 = 4).
    • Giới hạn:
      • (mathop {lim }limits{x to – infty } y = mathop {lim }limits{x to – infty } (2 + 3x – x^3) = mathop {lim }limits_{x to – infty } (-x^3) = +infty).
      • (mathop {lim }limits{x to + infty } y = mathop {lim }limits{x to + infty } (2 + 3x – x^3) = mathop {lim }limits_{x to + infty } (-x^3) = -infty).

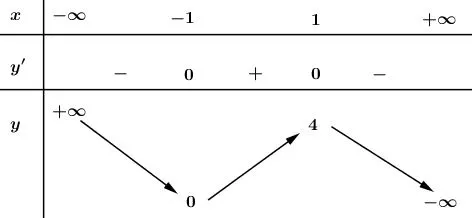
  3. Bảng biến thiên:

    (x)(-infty)-11(+infty)
    (y’)–0+0
    (y)(+infty)(searrow)(0)(nearrow)

  4. Đồ thị:

    • Giao trục Oy: Cho (x=0 Rightarrow y=2). Giao điểm là ((0, 2)).
    • Giao trục Ox: Giải (y=0 Leftrightarrow 2 + 3x – x^3 = 0).
      Phương trình này có nghiệm là (x=2) và (x=-1) (nghiệm kép, vì tại (x=-1), (y_{CT}=0)).
      Do đó, đồ thị tiếp xúc với trục hoành tại ((-1, 0)) và cắt trục hoành tại ((2, 0)).
    • Điểm uốn (tâm đối xứng):
      (y” = -6x).
      (y” = 0 Leftrightarrow -6x = 0 Leftrightarrow x = 0).
      Tại (x=0), (y = 2 + 3(0) – (0)^3 = 2).
      Điểm uốn là (I(0, 2)).
    • Vẽ đồ thị: Dựa vào bảng biến thiên, các điểm cực trị ((-1, 0)), ((1, 4)), điểm uốn ((0, 2)) và các giao điểm với trục hoành ((-1, 0)) (tiếp xúc) và ((2, 0)).

Câu b) (y = x^3 + 4x^2 + 4x)

  1. TXĐ: (D = mathbb{R}).

  2. Sự biến thiên:

    • Đạo hàm: (y’ = 3x^2 + 8x + 4).
    • Các điểm dừng: (y’ = 0 Leftrightarrow 3x^2 + 8x + 4 = 0).
      Delta ( = 8^2 – 4(3)(4) = 64 – 48 = 16).
      (x = frac{-8 pm sqrt{16}}{2(3)} = frac{-8 pm 4}{6}).
      (x_1 = frac{-8-4}{6} = frac{-12}{6} = -2).
      (x_2 = frac{-8+4}{6} = frac{-4}{6} = -frac{2}{3}).
    • Xét dấu (y’) và chiều biến thiên: (y’) là một tam thức bậc hai có hệ số (a=3>0), nên (y’) dương ngoài khoảng hai nghiệm (left(-2, -frac{2}{3}right)) và âm trong khoảng hai nghiệm.
      • Trên (left( -infty, -2 right)), (y’ > 0), hàm số đồng biến.
      • Trên (left( -2, -frac{2}{3} right)), (y’ < 0), hàm số nghịch biến.
      • Trên (left( -frac{2}{3}, +infty right)), (y’ > 0), hàm số đồng biến.
    • Cực trị:
      • Tại (x = -2), (y’) đổi dấu từ (+rightarrow -). Hàm số đạt cực đại. (y_{CD} = y(-2) = (-2)^3 + 4(-2)^2 + 4(-2) = -8 + 4(4) – 8 = -8 + 16 – 8 = 0).
      • Tại (x = -frac{2}{3}), (y’) đổi dấu từ (- rightarrow +). Hàm số đạt cực tiểu. (y_{CT} = yleft(-frac{2}{3}right) = left(-frac{2}{3}right)^3 + 4left(-frac{2}{3}right)^2 + 4left(-frac{2}{3}right) = -frac{8}{27} + 4left(frac{4}{9}right) – frac{8}{3} = -frac{8}{27} + frac{16}{9} – frac{8}{3} = frac{-8 + 48 – 72}{27} = -frac{32}{27}).
    • Giới hạn:
      • (mathop {lim }limits{x to – infty } y = mathop {lim }limits{x to – infty } (x^3 + 4x^2 + 4x) = mathop {lim }limits_{x to – infty } x^3 = -infty).
      • (mathop {lim }limits{x to + infty } y = mathop {lim }limits{x to + infty } (x^3 + 4x^2 + 4x) = mathop {lim }limits_{x to + infty } x^3 = +infty).

  3. Bảng biến thiên:

    (x)(-infty)-2(-frac{2}{3})(+infty)
    (y’)+0–0
    (y)(-infty)(nearrow)(0)(searrow)

  4. Đồ thị:

    • Giao trục Oy: Cho (x=0 Rightarrow y=0). Giao điểm là ((0, 0)).
    • Giao trục Ox: Giải (y=0 Leftrightarrow x^3 + 4x^2 + 4x = 0).
      (x(x^2 + 4x + 4) = 0)
      (x(x+2)^2 = 0).
      Nghiệm là (x=0) và (x=-2) (nghiệm kép).
      Đồ thị cắt trục hoành tại ((0, 0)) và tiếp xúc với trục hoành tại ((-2, 0)).
    • Điểm uốn (tâm đối xứng):
      (y’ = 3x^2 + 8x + 4).
      (y” = 6x + 8).
      (y” = 0 Leftrightarrow 6x + 8 = 0 Leftrightarrow x = -frac{8}{6} = -frac{4}{3}).
      Tại (x = -frac{4}{3}), (y = left(-frac{4}{3}right)^3 + 4left(-frac{4}{3}right)^2 + 4left(-frac{4}{3}right) = -frac{64}{27} + 4left(frac{16}{9}right) – frac{16}{3} = -frac{64}{27} + frac{64}{9} – frac{16}{3} = frac{-64 + 192 – 144}{27} = -frac{16}{27}).
      Điểm uốn là (Ileft(-frac{4}{3}, -frac{16}{27}right)).
    • Vẽ đồ thị: Dựa vào bảng biến thiên, các điểm cực trị ((-2, 0)), (left(-frac{2}{3}, -frac{32}{27}right)), điểm uốn (Ileft(-frac{4}{3}, -frac{16}{27}right)), giao điểm ((0, 0)) và tiếp xúc tại ((-2, 0)).

Câu c) (y = x^3 + x^2 + 9x)

  1. TXĐ: (D = mathbb{R}).

  2. Sự biến thiên:

    • Đạo hàm: (y’ = 3x^2 + 2x + 9).
    • Các điểm dừng: Xét (y’ = 0 Leftrightarrow 3x^2 + 2x + 9 = 0).
      Delta ( = 2^2 – 4(3)(9) = 4 – 108 = -104 < 0).
      Do (y’) là tam thức bậc hai có hệ số (a=3>0) và Delta ( < 0), nên (y’ > 0) với mọi (x in mathbb{R}).
    • Chiều biến thiên: Hàm số luôn đồng biến trên (mathbb{R}).
    • Cực trị: Hàm số không có cực trị vì đạo hàm không đổi dấu.
    • Giới hạn:
      • (mathop {lim }limits{x to – infty } y = mathop {lim }limits{x to – infty } (x^3 + x^2 + 9x) = mathop {lim }limits_{x to – infty } x^3 = -infty).
      • (mathop {lim }limits{x to + infty } y = mathop {lim }limits{x to + infty } (x^3 + x^2 + 9x) = mathop {lim }limits_{x to + infty } x^3 = +infty).

  3. Bảng biến thiên:

    (x)(-infty)+(+infty)
    (y’)+++
    (y)(-infty)(nearrow)(+infty)

  4. Đồ thị:

    • Giao trục Oy: Cho (x=0 Rightarrow y=0). Giao điểm là ((0, 0)).
    • Giao trục Ox: Giải (y=0 Leftrightarrow x^3 + x^2 + 9x = 0).
      (x(x^2 + x + 9) = 0).
      Phương trình (x^2 + x + 9 = 0) có Delta ( = 1^2 – 4(1)(9) = 1 – 36 = -35 < 0). Nên (x=0) là nghiệm duy nhất.
      Đồ thị chỉ cắt trục hoành tại gốc tọa độ ((0, 0)).
    • Điểm uốn (tâm đối xứng):
      (y” = 6x + 2).
      (y” = 0 Leftrightarrow 6x + 2 = 0 Leftrightarrow x = -frac{2}{6} = -frac{1}{3}).
      Tại (x = -frac{1}{3}), (y = left(-frac{1}{3}right)^3 + left(-frac{1}{3}right)^2 + 9left(-frac{1}{3}right) = -frac{1}{27} + frac{1}{9} – 3 = frac{-1 + 3 – 81}{27} = -frac{79}{27}).
      Điểm uốn là (Ileft(-frac{1}{3}, -frac{79}{27}right)).
    • Vẽ đồ thị: Dựa vào bảng biến thiên, đồ thị luôn đồng biến, đi qua gốc tọa độ ((0, 0)), và có điểm uốn (Ileft(-frac{1}{3}, -frac{79}{27}right)). Ta có thể tính thêm một vài điểm như (x=-1 Rightarrow y = -1+1-9 = -9), (( -1, -9 )).

Câu d) (y = -2x^3 + 5)

  1. TXĐ: (D = mathbb{R}).

  2. Sự biến thiên:

    • Đạo hàm: (y’ = -6x^2).
    • Các điểm dừng: (y’ = 0 Leftrightarrow -6x^2 = 0 Leftrightarrow x = 0).
    • Xét dấu (y’) và chiều biến thiên:
      (y’ = -6x^2 le 0) với mọi (x in mathbb{R}). (y’=0) chỉ tại (x=0), còn lại (y'<0).
      • Trên (left( -infty, 0 right)), (y’ < 0), hàm số nghịch biến.
      • Trên (left( 0, +infty right)), (y’ < 0), hàm số nghịch biến.
        Hàm số luôn nghịch biến trên (mathbb{R}).
    • Cực trị: Tại (x=0), đạo hàm bằng 0 nhưng không đổi dấu qua (x=0). Do đó, hàm số không có cực trị.
    • Giới hạn:
      • (mathop {lim }limits{x to – infty } y = mathop {lim }limits{x to – infty } (-2x^3 + 5) = mathop {lim }limits_{x to – infty } (-2x^3) = +infty).
      • (mathop {lim }limits{x to + infty } y = mathop {lim }limits{x to + infty } (-2x^3 + 5) = mathop {lim }limits_{x to + infty } (-2x^3) = -infty).

  3. Bảng biến thiên:

    (x)(-infty)0(+infty)
    (y’)–0–
    (y)(+infty)(searrow)(5)

  4. Đồ thị:

    • Giao trục Oy: Cho (x=0 Rightarrow y = -2(0)^3 + 5 = 5). Giao điểm là ((0, 5)).
    • Giao trục Ox: Giải (y=0 Leftrightarrow -2x^3 + 5 = 0 Leftrightarrow x^3 = frac{5}{2} Leftrightarrow x = sqrt[3]{frac{5}{2}}).
      Đồ thị cắt trục hoành tại (left( sqrt[3]{frac{5}{2}}, 0 right)).
    • Điểm uốn (tâm đối xứng):
      (y’ = -6x^2).
      (y” = -12x).
      (y” = 0 Leftrightarrow -12x = 0 Leftrightarrow x = 0).
      Tại (x=0), (y = -2(0)^3 + 5 = 5).
      Điểm uốn là (I(0, 5)) (chính là giao điểm với trục Oy).
    • Vẽ đồ thị: Dựa vào bảng biến thiên, đồ thị luôn nghịch biến, đi qua ((0, 5)) và (left( sqrt[3]{frac{5}{2}}, 0 right)).

Đáp Án/Kết Quả

Qua quá trình khảo sát chi tiết, chúng ta đã xác định được sự biến thiên, các điểm cực trị (nếu có), giới hạn, giao điểm với các trục tọa độ và điểm uốn cho từng hàm số. Các bảng biến thiên và đồ thị được phác thảo chính xác, cung cấp cái nhìn trực quan về hành vi của từng hàm số bậc ba cụ thể. Mỗi hàm số có đặc điểm riêng biệt, từ đồng biến trên toàn R, có hai cực trị, đến trường hợp chỉ có một điểm uốn và luôn đồng biến/nghịch biến.

Kết Luận

Nắm vững quy trình khảo sát sự biến thiên và vẽ đồ thị hàm số bậc ba là kỹ năng thiết yếu đối với học sinh lớp 12. Bài viết này đã trình bày một cách có hệ thống các bước từ cơ bản đến nâng cao, bao gồm việc tính toán đạo hàm, phân tích dấu đạo hàm, xác định cực trị, tính giới hạn, lập bảng biến thiên và cuối cùng là phác thảo đồ thị dựa trên các thông tin đã thu thập. Việc luyện tập thường xuyên với nhiều dạng bài khác nhau sẽ giúp bạn đọc củng cố kiến thức và giải quyết thành công mọi bài toán liên quan đến chủ đề này.

Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông

You may also like...

Leave a Reply

Your email address will not be published. Required fields are marked *

Kênh Xoilac TV HD ngon