Đề thi học sinh giỏi các môn - chuyên đề bồi dưỡng HSG miễn phí

Sách Giải Toán Lớp 9 Tập 2: Hướng Dẫn Chi Tiết Và Chuẩn Xác

by · January 7, 2026

Rate this post

Được biên soạn bám sát nội dung sách bài tập Toán lớp 9, loạt bài sách giải toán lớp 9 tập 2 cung cấp cho học sinh những lời giải chi tiết, công phu và chính xác nhất. Mục tiêu là giúp các em dễ dàng tiếp cận, nắm vững kiến thức và tự tin chinh phục mọi bài tập Toán học. Loạt bài này không chỉ giải bài tập mà còn phân tích sâu sắc từng bước làm, cung cấp kiến thức nền tảng và mẹo kiểm tra, đảm bảo học sinh không chỉ làm được bài mà còn hiểu bản chất.

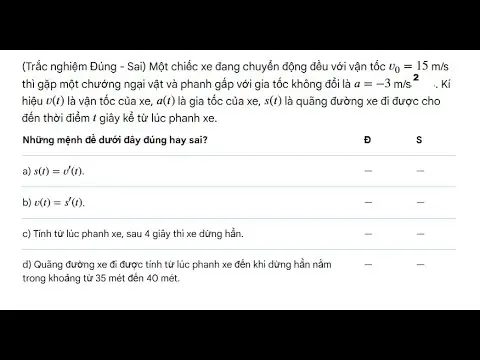
Đề Bài

Dưới đây là các bài tập được trích từ sách bài tập Toán lớp 9 tập 2, bao gồm các phần Đại số và Hình học.

Bài 1 trang 5 Sách bài tập Toán 9 Tập 2: Phương trình bậc nhất hai ẩn

Cho các cặp số và các phương trình sau. Hãy dùng mũi tên (như trong hình vẽ) chỉ rõ mỗi cặp số là nghiệm của những phương trình nào?

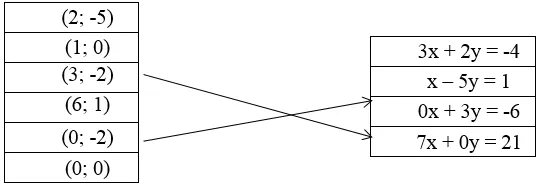Cặp số và phương trình Toán lớp 9Cặp số và phương trình Toán lớp 9Biểu diễn mối quan hệ giữa cặp số và phương trìnhBiểu diễn mối quan hệ giữa cặp số và phương trình

Bài 2 trang 5 Sách bài tập Toán 9 Tập 2: Phương trình bậc nhất hai ẩn

Viết nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của mỗi phương trình sau:
a. 2x – y = 3
b. x + 2y = 4
c. 3x – 2y = 6
d. 2x + 3y = 5
e. 0x + 5y = -10
f. -4x + 0y = -12

Bài 3 trang 5 Sách bài tập Toán 9 Tập 2: Phương trình bậc nhất hai ẩn

Trong mỗi trường hợp sau, hãy tìm giá trị của m để:
a. Điểm M(1; 0) thuộc đường thẳng mx – 5y = 7;
b. Điểm N(0; -3) thuộc đường thẳng 2,5x + my = -21;
c. Điểm P(5; -3) thuộc đường thẳng mx + 2y = -1;
d. Điểm P(5; -3) thuộc đường thẳng 3x – my = 6;
e. Điểm Q(0,5; -3) thuộc đường thẳng mx + 0y = 17,5;
f. Điểm S(4; 0,3) thuộc đường thẳng 0x + my = 1,5;
g. Điểm A(2; -3) thuộc đường thẳng (m – 1)x + (m + 1)y = 2m +1.

Bài 4 trang 6 Sách bài tập Toán 9 Tập 2: Phương trình bậc nhất hai ẩn

Phương trình nào sau đây xác định một hàm số dạng y = ax + b.
a. 5x – y = 7;
b. 3x + 5y = 10;
c. 0x + 3y = -1;
d. 6x – 0y = 18.

Bài 1 trang 99 Sách bài tập Toán 9 Tập 2: Góc ở tâm – Số đo cung

a. Từ 1 giờ đến 3 giờ thì kim giờ quay được một góc ở tâm bằng bao nhiêu độ?
b. Từ 3 giờ đến 6 giờ thì kim giờ quay được một góc ở tâm bằng bao nhiêu độ?

Bài 2 trang 99 Sách bài tập Toán 9 Tập 2: Góc ở tâm – Số đo cung

Một đồng hồ chạy chậm 25 phút. Hỏi để chỉnh lại đúng giờ thì phải quay kim phút một góc ở tâm là bao nhiêu độ?

Bài 3 trang 99 Sách bài tập Toán 9 Tập 2: Góc ở tâm – Số đo cung

Hãy xếp một tờ giấy để cắt thành một hình ngôi sao năm cánh đều nhau. Muốn cắt chỉ bằng một nhát kéo thì phải gấp tờ giấy đó thành một hình có góc ở tâm bằng bao nhiêu độ?

Bài 4 trang 99 Sách bài tập Toán 9 Tập 2: Góc ở tâm – Số đo cung

Hai tiếp tuyến tại A,B của đường tròn (O ;R) cắt nhau tại M. Biết OM =2R. Tính số đo của góc ở tâm AOB?

Tam giác vuông OMA và đường trònTam giác vuông OMA và đường trònQuan hệ giữa OM, R và góc AOBQuan hệ giữa OM, R và góc AOB

Bài 5 trang 99 Sách bài tập Toán 9 Tập 2: Góc ở tâm – Số đo cung

Cho đường tròn (O;R), đường kính AB. Gọi C là điểm chính giữa của cung AB. Vẽ dây CD dài bằng R. Tính góc ở tâm BOD. Có mấy đáp số?

Hình tròn với dây CD và các gócHình tròn với dây CD và các góc

Phân Tích Yêu Cầu

Phần này của sách giải toán lớp 9 tập 2 tập trung vào việc làm rõ yêu cầu của từng bài toán, xác định các dữ kiện quan trọng và định hướng phương pháp giải chung. Học sinh cần hiểu rõ đề bài hỏi gì, cho gì và mối liên hệ giữa chúng để có thể tiếp cận bài toán một cách hiệu quả.

Kiến Thức/Nền Tảng Cần Dùng

Để giải quyết các bài tập trong chương trình Toán lớp 9 tập 2, học sinh cần nắm vững các kiến thức cơ bản sau:

Đại số: Phương trình bậc nhất hai ẩn

  • Định nghĩa: Phương trình bậc nhất hai ẩn có dạng tổng quát là ax + by = c, trong đó a, b, c là các hệ số, x và y là hai ẩn số.
  • Nghiệm của phương trình: Một cặp số (x₀; y₀) được gọi là một nghiệm của phương trình ax + by = c nếu khi thay x₀ vào x và y₀ vào y thì phương trình đúng.
  • Tập nghiệm: Phương trình bậc nhất hai ẩn ax + by = c (với a hoặc b khác 0) luôn có vô số nghiệm. Tập nghiệm được biểu diễn bởi một đường thẳng trong mặt phẳng tọa độ.
  • Biểu diễn tập nghiệm: Để biểu diễn tập nghiệm, ta có thể tìm hai điểm bất kỳ thuộc đường thẳng đó. Ví dụ:
    • Cho x = 0, tìm y. Ta được điểm (0; y₀).
    • Cho y = 0, tìm x. Ta được điểm (x₀; 0).
    • Hoặc chọn một giá trị bất kỳ cho x (hoặc y), rồi tính giá trị tương ứng của ẩn còn lại.
  • Trường hợp đặc biệt:
    • Nếu a = 0, phương trình trở thành by = c. Nếu b ≠ 0, thì y = c/b. Đây là đường thẳng song song với trục Ox (nếu c/b ≠ 0) hoặc trùng với trục Ox (nếu c/b = 0).
    • Nếu b = 0, phương trình trở thành ax = c. Nếu a ≠ 0, thì x = c/a. Đây là đường thẳng song song với trục Oy (nếu c/a ≠ 0) hoặc trùng với trục Oy (nếu c/a = 0).
    • Nếu a = 0 và b = 0, phương trình trở thành 0 = c. Nếu c = 0, phương trình có vô số nghiệm. Nếu c ≠ 0, phương trình vô nghiệm.

Hình học: Góc ở tâm và Số đo cung

  • Góc ở tâm: Là góc có đỉnh trùng với tâm của đường tròn.
  • Số đo cung: Số đo của cung được xác định bằng số đo của góc ở tâm chắn cung đó.
  • Đơn vị đo: Số đo cung được tính bằng độ (°) hoặc radian. Trong chương trình này, ta chủ yếu làm việc với đơn vị độ.
  • Tính chất:
    • Số đo cung nhỏ bằng số đo góc ở tâm chắn cung đó.
    • Số đo cung lớn bằng 360° trừ đi số đo cung nhỏ.
    • Đường kính chia đường tròn thành hai cung có số đo bằng 180°.
    • Hai cung bằng nhau thì chắn các góc ở tâm bằng nhau và ngược lại.
  • Ứng dụng: Các bài toán về đồng hồ, hình ngôi sao, và các bài toán liên quan đến tính toán góc trong đường tròn.

Hướng Dẫn Giải Chi Tiết

Bài 1 trang 5 Sách bài tập Toán 9 Tập 2: Phương trình bậc nhất hai ẩn

Để xác định xem cặp số nào là nghiệm của phương trình nào, ta lần lượt thay tọa độ của từng cặp số vào các phương trình và kiểm tra xem phương trình có đúng hay không.

Ví dụ với cặp số (2; -1):

  • Kiểm tra với phương trình 2x – y = 3: Thay x=2, y=-1 vào, ta có 2(2) - (-1) = 4 + 1 = 5. Vì 5 ≠ 3, nên cặp (2; -1) không phải là nghiệm của phương trình này.
  • Kiểm tra với phương trình x + 2y = 4: Thay x=2, y=-1 vào, ta có 2 + 2(-1) = 2 - 2 = 0. Vì 0 ≠ 4, nên cặp (2; -1) không phải là nghiệm của phương trình này.
  • Kiểm tra với phương trình 3x – 2y = 6: Thay x=2, y=-1 vào, ta có 3(2) - 2(-1) = 6 + 2 = 8. Vì 8 ≠ 6, nên cặp (2; -1) không phải là nghiệm của phương trình này.
  • Kiểm tra với phương trình 2x + 3y = 5: Thay x=2, y=-1 vào, ta có 2(2) + 3(-1) = 4 - 3 = 1. Vì 1 ≠ 5, nên cặp (2; -1) không phải là nghiệm của phương trình này.

Ta cần thực hiện phép kiểm tra tương tự cho tất cả các cặp số và tất cả các phương trình để nối chúng lại một cách chính xác.

Lời giải bài 1 trang 5Lời giải bài 1 trang 5

Bài 2 trang 5 Sách bài tập Toán 9 Tập 2: Phương trình bậc nhất hai ẩn

Để tìm nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm, ta làm như sau:

Các bước chung:

  1. Chọn một ẩn tùy ý (ví dụ: đặt x = t, với t là tham số).
  2. Biểu diễn ẩn còn lại theo t.
  3. Viết nghiệm tổng quát dưới dạng (x; y) = (x(t); y(t)).
  4. Để vẽ đường thẳng, chọn hai giá trị khác nhau cho t (ví dụ: t=0 và t=1), tìm hai cặp (x, y) tương ứng.
  5. Vẽ đường thẳng đi qua hai điểm này.

Ví dụ với câu a: 2x – y = 3

  1. Chọn x = t.
  2. Từ phương trình: y = 2x - 3, thay x=t ta có y = 2t - 3.
  3. Nghiệm tổng quát là: (t; 2t - 3).
  4. Chọn t = 0: x = 0, y = 2(0) - 3 = -3. Ta được điểm (0; -3).
  5. Chọn t = 1: x = 1, y = 2(1) - 3 = -1. Ta được điểm (1; -1).
  6. Vẽ đường thẳng đi qua hai điểm (0; -3) và (1; -1).

Lời giải câu a bài 2 trang 5Lời giải câu a bài 2 trang 5 Lời giải câu a bài 2 trang 5 (tiếp)Lời giải câu a bài 2 trang 5 (tiếp)

Ví dụ với câu e: 0x + 5y = -10

  1. Đây là trường hợp a = 0. Phương trình trở thành 5y = -10, suy ra y = -2.
  2. Ẩn x có thể nhận bất kỳ giá trị nào. Ta có thể chọn x = t.
  3. Nghiệm tổng quát là: (t; -2).
  4. Chọn t = 0: x = 0, y = -2. Ta được điểm (0; -2).
  5. Chọn t = 1: x = 1, y = -2. Ta được điểm (1; -2).
  6. Đường thẳng đi qua hai điểm (0; -2) và (1; -2) là đường thẳng ngang y = -2, song song với trục Ox.

Lời giải câu e bài 2 trang 5Lời giải câu e bài 2 trang 5

Ví dụ với câu f: -4x + 0y = -12

  1. Đây là trường hợp b = 0. Phương trình trở thành -4x = -12, suy ra x = 3.
  2. Ẩn y có thể nhận bất kỳ giá trị nào. Ta có thể chọn y = t.
  3. Nghiệm tổng quát là: (3; t).
  4. Chọn t = 0: x = 3, y = 0. Ta được điểm (3; 0).
  5. Chọn t = 1: x = 3, y = 1. Ta được điểm (3; 1).
  6. Đường thẳng đi qua hai điểm (3; 0) và (3; 1) là đường thẳng đứng x = 3, song song với trục Oy.

Lời giải câu f bài 2 trang 5Lời giải câu f bài 2 trang 5

Mẹo kiểm tra: Sau khi vẽ đường thẳng, thử chọn một điểm bất kỳ trên đường thẳng và thay tọa độ của nó vào phương trình ban đầu để xem có đúng không.
Lỗi hay gặp:

  • Tính toán sai khi biểu diễn một ẩn theo ẩn kia.
  • Chọn hai điểm trùng nhau, dẫn đến không xác định được đường thẳng.
  • Vẽ sai đường thẳng hoặc quên vẽ trục tọa độ, nhãn trục.

Bài 3 trang 5 Sách bài tập Toán 9 Tập 2: Phương trình bậc nhất hai ẩn

Nguyên tắc cơ bản để giải các bài toán này là: Nếu một điểm thuộc một đường thẳng, thì tọa độ của điểm đó phải là nghiệm của phương trình đường thẳng đó. Tức là, khi thay tọa độ của điểm vào phương trình, ta sẽ nhận được một đẳng thức đúng.

Ví dụ với câu a: Điểm M(1; 0) thuộc đường thẳng mx – 5y = 7

  • Thay tọa độ điểm M(1; 0) vào phương trình đường thẳng:
    m(1) - 5(0) = 7
  • Giải phương trình tìm m:
    m - 0 = 7
    m = 7
  • Vậy, với m = 7, đường thẳng 7x - 5y = 7 đi qua điểm M(1; 0).

Ví dụ với câu g: Điểm A(2; -3) thuộc đường thẳng (m – 1)x + (m + 1)y = 2m +1

  • Thay tọa độ điểm A(2; -3) vào phương trình đường thẳng:
    (m - 1)(2) + (m + 1)(-3) = 2m + 1
  • Giải phương trình tìm m:
    2m - 2 - 3m - 3 = 2m + 1
    -m - 5 = 2m + 1
    3m = -6
    m = -2
  • Vậy, với m = -2, đường thẳng (-2 - 1)x + (-2 + 1)y = 2(-2) + 1 hay -3x - y = -3 đi qua điểm A(2; -3).

Mẹo kiểm tra: Sau khi tìm được giá trị của m, thay giá trị đó vào phương trình đường thẳng ban đầu, sau đó thay tọa độ điểm đã cho vào phương trình vừa tìm được. Nếu đẳng thức đúng, kết quả m là chính xác.
Lỗi hay gặp:

  • Nhầm lẫn khi thay tọa độ của điểm vào phương trình.
  • Sai sót trong quá trình biến đổi đại số khi giải phương trình tìm m.

Bài 4 trang 6 Sách bài tập Toán 9 Tập 2: Phương trình bậc nhất hai ẩn

Một phương trình xác định một hàm số dạng y = ax + b khi và chỉ khi ta có thể rút ra y theo x một cách duy nhất. Điều này có nghĩa là hệ số của y (trong phương trình tổng quát Ax + By = C) phải khác 0.

  • Câu a: 5x – y = 7
    Ta có thể rút y ra: y = 5x - 7. Đây là hàm số dạng y = ax + b với a = 5 và b = -7.
  • Câu b: 3x + 5y = 10
    Ta có thể rút y ra: 5y = -3x + 10, suy ra y = (-frac{3}{5})x + 2. Đây là hàm số dạng y = ax + b với a = -frac{3}{5} và b = 2.
  • Câu c: 0x + 3y = -1
    Ta có thể rút y ra: 3y = -1, suy ra y = -frac{1}{3}. Đây là hàm số dạng y = ax + b với a = 0 và b = -frac{1}{3} (đây là hàm hằng).
  • Câu d: 6x – 0y = 18
    Phương trình trở thành 6x = 18, suy ra x = 3. Trong trường hợp này, x luôn bằng 3, không phụ thuộc vào y. Ta không thể biểu diễn y theo x theo dạng y = ax + b. Đây là một đường thẳng đứng song song với trục Oy.

Kết luận: Các phương trình a, b, c đều xác định hàm số dạng y = ax + b. Phương trình d thì không.

Mẹo kiểm tra: Luôn nhớ rằng hàm số y = ax + b có nghĩa là với mỗi giá trị của x, ta chỉ tìm được duy nhất một giá trị của y. Nếu phương trình cho phép y có nhiều giá trị với một x, hoặc nếu phương trình chỉ cho giá trị cố định của x (không phụ thuộc y), thì đó không phải là hàm số dạng y = ax + b.

Bài 1 trang 99 Sách bài tập Toán 9 Tập 2: Góc ở tâm – Số đo cung

Trên mặt đồng hồ có 12 số, chia đường tròn thành 12 phần bằng nhau. Mỗi phần tương ứng với một góc ở tâm là 360° / 12 = 30°.

  • Câu a: Từ 1 giờ đến 3 giờ
    Kim giờ di chuyển qua 3 - 1 = 2 khoảng.
    Góc ở tâm kim giờ quay được là: 2 times 30° = 60°.
  • Câu b: Từ 3 giờ đến 6 giờ
    Kim giờ di chuyển qua 6 - 3 = 3 khoảng.
    Góc ở tâm kim giờ quay được là: 3 times 30° = 90°.

Mẹo kiểm tra: Tưởng tượng kim giờ di chuyển trên mặt đồng hồ và đếm số khoảng cách giữa các giờ.

Bài 2 trang 99 Sách bài tập Toán 9 Tập 2: Góc ở tâm – Số đo cung

Kim phút quay một vòng 360° trong 60 phút.
Vậy, mỗi phút, kim phút quay được một góc ở tâm là 360° / 60 = 6°.

Đồng hồ chạy chậm 25 phút, có nghĩa là kim phút cần phải quay thêm 25 phút nữa để cập nhật đúng thời gian.
Do đó, để chỉnh lại đúng giờ, kim phút phải quay một góc ở tâm là:
25 text{ phút} times 6°/text{phút} = 150°.

Mẹo kiểm tra: Kiểm tra lại phép nhân. 25 6 = 150.

Bài 3 trang 99 Sách bài tập Toán 9 Tập 2: Góc ở tâm – Số đo cung

Để cắt một hình ngôi sao năm cánh đều nhau chỉ bằng một nhát kéo, tờ giấy cần được gấp sao cho các cạnh sẽ cắt tạo thành hình ngôi sao có 5 đỉnh đối xứng.

  • Một hình ngôi sao 5 cánh đều có 5 đỉnh và 5 cánh đối xứng.
  • Khi gấp tờ giấy để chuẩn bị cắt, ta cần tạo ra các góc tại tâm sao cho khi cắt một đường thẳng duy nhất, nó sẽ giao với các cạnh đã gấp để tạo thành 5 cánh đều nhau.
  • Tổng số đo các góc ở tâm tạo thành một đường tròn là 360°.
  • Để có 5 cánh đều nhau, ta chia đều góc ở tâm cho 5 phần.
  • Góc ở tâm cho mỗi phần sẽ là 360° / 5 = 72°.

Tuy nhiên, cách cắt hình ngôi sao bằng một nhát kéo thường liên quan đến việc gấp giấy theo các góc tạo thành các tam giác cân hoặc đều, và đường cắt sẽ đi qua hai điểm trên chu vi. Nếu ta gấp giấy sao cho các cạnh của hình sao tương lai nằm trên các đường thẳng cách đều nhau từ tâm, thì góc ở tâm giữa hai đường liên tiếp sẽ là 360° / 5 = 72°.
Một phương pháp phổ biến để cắt hình ngôi sao năm cánh là gấp giấy thành hình nón hoặc đa giác đều. Nếu ta gấp giấy làm 5 phần bằng nhau, mỗi phần sẽ có góc ở tâm là 360° / 5 = 72°. Tuy nhiên, cách gấp để cắt một nhát kéo thường liên quan đến việc tạo ra các cạnh bằng nhau và các góc bằng nhau trên mặt phẳng.

Xem lại cách giải gốc: “chia tờ giấy đã gấp ra 5 phần với 5 góc ở tâm bằng nhau, mỗi góc bằng 180 :5 =36°”. Điều này ám chỉ việc gấp đôi tờ giấy trước, sau đó chia 180 độ (của nửa vòng tròn) thành 5 phần.

  • Gấp đôi tờ giấy: ta có một nửa vòng tròn (180°).
  • Chia 180° này thành 5 phần bằng nhau: 180° / 5 = 36°.
  • Khi mở tờ giấy ra, mỗi góc ở tâm này sẽ nhân đôi, tạo thành góc của hình ngôi sao hoặc góc giữa các tia phân giác của các góc ở tâm của hình sao.
    Nếu mỗi phần là 36°, khi mở ra thì 36° times 2 = 72°.

Ta cần làm rõ hơn về cách gấp. Phương pháp phổ biến để cắt ngôi sao 5 cánh bằng một nhát kéo thường liên quan đến việc gấp một dải giấy dài. Nếu coi tâm của ngôi sao là đỉnh, thì 5 đỉnh của ngôi sao chia đường tròn thành 5 cung bằng nhau. Góc ở tâm chắn các cung này là 360°/5 = 72°. Tuy nhiên, cách gấp giấy để cắt một nhát có thể tạo ra các góc khác nhau.
Theo cách giải sách giải toán lớp 9 tập 2, người ta gấp đôi tờ giấy rồi chia 180° ra 5 phần, mỗi phần 36°. Đây là cách gấp đặc trưng.

Lời giải:
Để cắt hình ngôi sao năm cánh đều bằng một nhát kéo, ta cần gấp tờ giấy để tạo ra các góc tương ứng. Theo phương pháp phổ biến, sau khi gấp đôi tờ giấy, ta sẽ chia nửa vòng tròn (180°) thành 5 phần bằng nhau. Mỗi phần có số đo là 180° / 5 = 36°.

Bài 4 trang 99 Sách bài tập Toán 9 Tập 2: Góc ở tâm – Số đo cung

Cho đường tròn (O; R) và hai tiếp tuyến MA, MB cắt nhau tại M. Ta có OM là đường phân giác của góc AOB và góc AMB. OA perp MA, OB perp MB.
Xét tam giác OMA vuông tại A. Ta có OA = R và OM = 2R.
Ta có:
cos(angle AOM) = dfrac{OA}{OM} = dfrac{R}{2R} = dfrac{1}{2}.
Suy ra angle AOM = 60°.

Vì OM là phân giác của góc AOB, nên:
angle AOB = 2 times angle AOM = 2 times 60° = 120°.

Số đo góc ở tâm BOD: Bài toán hỏi góc AOB, không phải BOD. Giả sử đề bài muốn hỏi góc AOB.
Nếu câu hỏi là “góc ở tâm AOB“, thì đáp án là 120°.

Mẹo kiểm tra: Sử dụng các tỉ số lượng giác trong tam giác vuông để xác định góc. Nhớ rằng tam giác OMA là nửa của tam giác AOBM, và OM là tia phân giác của góc AOB.

Bài 5 trang 99 Sách bài tập Toán 9 Tập 2: Góc ở tâm – Số đo cung

Cho đường tròn (O; R) đường kính AB. C là điểm chính giữa cung AB. Dây CD có độ dài bằng R. Tính góc ở tâm BOD.

  • Vì AB là đường kính và C là điểm chính giữa cung AB, nên C nằm trên nửa đường tròn. Góc ACB là góc nội tiếp chắn nửa đường tròn, nên angle ACB = 90°.
  • C là điểm chính giữa cung AB, nên cung AC bằng cung CB. Mỗi cung này có số đo 180° / 2 = 90°. Do đó, angle AOC = angle BOC = 90°.
  • Tam giác AOC và BOC là các tam giác vuông cân tại O. AC = BC.
  • Ta có dây CD có độ dài bằng R.

Trường hợp 1: Điểm D nằm trên cung BC

  • Xét tam giác OCD. Ta có OC = OD = R (bán kính) và CD = R (theo đề bài).
  • Vậy, tam giác OCD đều.
  • Suy ra angle COD = 60°.
  • Góc ở tâm BOD là angle BOD = angle BOC - angle COD.
  • Vì angle BOC = 90° và angle COD = 60°, nên angle BOD = 90° - 60° = 30°.

Trường hợp 2: Điểm D nằm trên cung AC

  • Tương tự, xét tam giác OCD. Ta có OC = OD = R và CD = R.
  • Vậy, tam giác OCD đều.
  • Suy ra angle COD = 60°.
  • Góc ở tâm BOD là angle BOD = angle BOC + angle COD.
  • Vì angle BOC = 90° và angle COD = 60°, nên angle BOD = 90° + 60° = 150°.

Kết luận: Có hai đáp số cho góc ở tâm BOD là 30° và 150°.

Giải bài 5 trang 99Giải bài 5 trang 99

Mẹo kiểm tra: Vẽ hình cẩn thận với các trường hợp có thể xảy ra của điểm D. Kiểm tra xem tam giác OCD có thực sự đều hay không dựa trên độ dài các cạnh.

Đáp Án/Kết Quả

Bài 1 trang 5 Sách bài tập Toán 9 Tập 2: Phương trình bậc nhất hai ẩn

Các cặp số được nối với các phương trình tương ứng là nghiệm của chúng dựa trên phép kiểm tra tọa độ.

Bài 2 trang 5 Sách bài tập Toán 9 Tập 2: Phương trình bậc nhất hai ẩn

Nghiệm tổng quát và biểu diễn hình học (đường thẳng) của từng phương trình đã được xác định và vẽ như trong phần hướng dẫn chi tiết.

Bài 3 trang 5 Sách bài tập Toán 9 Tập 2: Phương trình bậc nhất hai ẩn

Các giá trị của m lần lượt là:
a. m = 7
b. m = 7
c. m = 1
d. m = -3
e. m = 35
f. m = 5
g. m = -2

Bài 4 trang 6 Sách bài tập Toán 9 Tập 2: Phương trình bậc nhất hai ẩn

Các phương trình xác định hàm số dạng y = ax + b là:
a. 5x – y = 7
b. 3x + 5y = 10
c. 0x + 3y = -1

Bài 1 trang 99 Sách bài tập Toán 9 Tập 2: Góc ở tâm – Số đo cung

a. Góc ở tâm kim giờ quay được từ 1 giờ đến 3 giờ là 60°.
b. Góc ở tâm kim giờ quay được từ 3 giờ đến 6 giờ là 90°.

Bài 2 trang 99 Sách bài tập Toán 9 Tập 2: Góc ở tâm – Số đo cung

Để chỉnh lại đúng giờ, kim phút phải quay một góc ở tâm là 150°.

Bài 3 trang 99 Sách bài tập Toán 9 Tập 2: Góc ở tâm – Số đo cung

Để cắt hình ngôi sao năm cánh đều bằng một nhát kéo, tờ giấy cần được gấp sao cho tương ứng với góc ở tâm là 36° (trên nửa vòng tròn đã gấp).

Bài 4 trang 99 Sách bài tập Toán 9 Tập 2: Góc ở tâm – Số đo cung

Số đo góc ở tâm AOB là 120°.

Bài 5 trang 99 Sách bài tập Toán 9 Tập 2: Góc ở tâm – Số đo cung

Có hai đáp số cho góc ở tâm BOD: 30° và 150°.

Conclusion

Loạt bài sách giải toán lớp 9 tập 2 này đã cung cấp lời giải chi tiết cho các bài tập quan trọng thuộc chủ đề phương trình bậc nhất hai ẩn và góc ở tâm – số đo cung. Bằng cách bám sát kiến thức sách giáo khoa và sách bài tập, chúng tôi đã phân tích từng bước giải, làm rõ các khái niệm nền tảng và đưa ra các mẹo kiểm tra hữu ích. Hy vọng rằng, thông qua các bài giải này, học sinh sẽ củng cố vững chắc kiến thức, rèn luyện kỹ năng giải toán và đạt được kết quả cao trong học tập môn Toán lớp 9.

Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông

You may also like...

Leave a Reply

Your email address will not be published. Required fields are marked *

Kênh Xoilac TV HD ngon