Giải Toán Lớp 5 Trang 143 Thời Gian

by Thầy Đông · January 7, 2026

Rate this post

Chào mừng bạn đến với bài viết chi tiết hướng dẫn giải toán lớp 5 trang 143 về chủ đề “Thời gian”. Bài viết này cung cấp các lời giải bài tập, phương pháp giải, kiến thức nền tảng và mẹo làm bài, giúp các em học sinh nắm vững kiến thức về thời gian trong chương trình Toán lớp 5 một cách hiệu quả. Chúng ta sẽ cùng nhau tìm hiểu cách tính thời gian, vận tốc, quãng đường và áp dụng vào các bài tập cụ thể.

Đề Bài

Dưới đây là các bài tập được trích nguyên văn từ sách giáo khoa Toán lớp 5, trang 143.

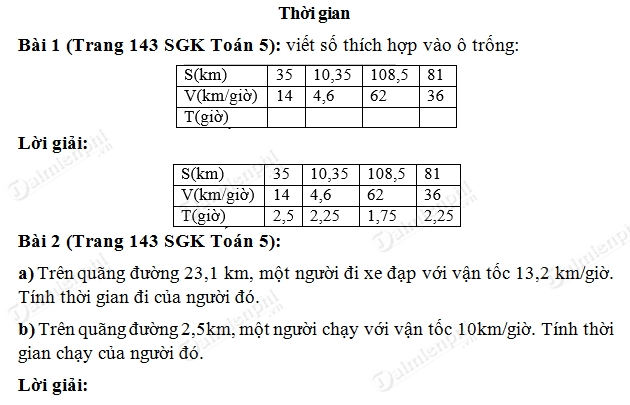
Bài 1: Viết số thích hợp vào ô trống:

s (km)	35	10,35	108,5	81
v (km/giờ)	14	4,6	62	36
t (giờ)

Lời giải:

s (km)	35	10,35	108,5	81
v (km/giờ)	14	4,6	62	36
t (giờ)	2,5	2,25	1,75	2,25

Bài 2:
a) Trên quãng đường 23,1 km, một người đi xe đạp với vận tốc 13,2 km/giờ. Tính thời gian đi của người đó.
b) Trên quãng đường 2,5 km, một người chạy với vận tốc 10 km/giờ. Tính thời gian chạy của người đó.

Lời giải:
a) Thời gian người đó đi là:
23,1 : 13,2 = 1,75 (giờ)
Đổi: 1,75 giờ = 1 giờ 45 phút

b) Thời gian chạy của người đó là:
2,5 : 10 = 0,25 (giờ)
Đổi: 0,25 giờ = 15 phút

Đáp số: a) 1 giờ 45 phút; b) 15 phút

Bài 3: Một máy bay bay với vận tốc 860 km/giờ được quãng đường 2150 km. Hỏi máy bay đến nơi lúc mấy giờ, nếu nó khởi hành lúc 8 giờ 45 phút?

Lời giải:
Thời gian máy bay bay là:
2150 : 860 = 2,5 (giờ)
Đổi: 2,5 giờ = 2 giờ 30 phút

Máy bay đến nơi lúc:
8 giờ 45 phút + 2 giờ 30 phút = 11 giờ 15 phút

Đáp số: 11 giờ 15 phút

Phân Tích Yêu Cầu

Các bài tập trên trang 143 chủ yếu xoay quanh việc tính toán liên quan đến thời gian, quãng đường và vận tốc trong chuyển động đều. Học sinh cần hiểu rõ mối quan hệ giữa ba đại lượng này để có thể giải quyết bài toán một cách chính xác.

Bài 1 yêu cầu điền vào bảng trống dựa trên các giá trị đã cho của quãng đường và vận tốc, hoặc ngược lại. Điều này giúp củng cố công thức cơ bản và khả năng áp dụng linh hoạt.
Bài 2 đưa ra các tình huống thực tế: một người đi xe đạp và một người chạy bộ. Học sinh cần tính thời gian tương ứng với quãng đường và vận tốc cho trước. Bài toán này cũng yêu cầu kỹ năng đổi đơn vị thời gian từ giờ sang giờ và phút.
Bài 3 là bài toán nâng cao hơn, yêu cầu tính thời điểm đến, biết thời điểm khởi hành, quãng đường và vận tốc. Bài toán này đòi hỏi sự kết hợp giữa việc tính thời gian di chuyển và cộng với thời gian bắt đầu hành trình.

Nhìn chung, các bài tập này đều tập trung vào việc áp dụng công thức tính thời gian trong chuyển động đều.

Kiến Thức/Nền Tảng Cần Dùng

Để giải quyết các bài toán về thời gian, quãng đường và vận tốc, chúng ta cần nắm vững các công thức cơ bản sau:

Công thức liên hệ giữa quãng đường, vận tốc và thời gian:
- Muốn tính quãng đường, ta lấy vận tốc nhân với thời gian:
  $s = v \times t$
- Muốn tính vận tốc, ta lấy quãng đường chia cho thời gian:
  $v = s : t$
- Muốn tính thời gian, ta lấy quãng đường chia cho vận tốc:
  $t = s : v$
Trong đó:
- $s$ : Quãng đường (đơn vị thường là km, m)
- $v$ : Vận tốc (đơn vị thường là km/giờ, m/giây, m/phút)
- $t$ : Thời gian (đơn vị thường là giờ, phút, giây)
Đơn vị đo thời gian:
Cần lưu ý các mối quan hệ giữa các đơn vị đo thời gian:
- 1 giờ = 60 phút
- 1 phút = 60 giây
- 1 giờ = 3600 giây
Khi làm bài toán, đơn vị của quãng đường và vận tốc phải tương ứng với nhau để phép tính cho ra kết quả đúng. Ví dụ, nếu quãng đường đo bằng km và vận tốc đo bằng km/giờ, thì thời gian sẽ có đơn vị là giờ. Nếu đơn vị không tương ứng, chúng ta cần thực hiện phép đổi đơn vị trước khi tính toán.
Tính thời điểm:
Để tìm thời điểm đến, ta lấy thời điểm khởi hành cộng với thời gian di chuyển. Nếu có thời gian nghỉ, ta cộng thêm cả thời gian nghỉ đó vào.
- Thời điểm đến = Thời điểm khởi hành + Thời gian di chuyển (+ Thời gian nghỉ nếu có)

Hướng Dẫn Giải Chi Tiết

Bây giờ, chúng ta sẽ đi vào giải chi tiết từng bài tập.

Bài 1: Điền số thích hợp vào ô trống

Bài tập này đòi hỏi việc áp dụng linh hoạt công thức $t = s : v$ . Chúng ta sẽ lần lượt tính giá trị thời gian $t$ cho từng cột.

Cột 1: $s = 35$ km, $v = 14$ km/giờ.
Thời gian $t = 35 : 14$ .
Thực hiện phép chia: $35 div 14 = 2,5$ (giờ).
Vậy, thời gian là 2,5 giờ.
Cột 2: $s = 10,35$ km, $v = 4,6$ km/giờ.
Thời gian $t = 10,35 : 4,6$ .
Thực hiện phép chia: $10,35 div 4,6 = 2,25$ (giờ).
Vậy, thời gian là 2,25 giờ.
Cột 3: $s = 108,5$ km, $v = 62$ km/giờ.
Thời gian $t = 108,5 : 62$ .
Thực hiện phép chia: $108,5 div 62 = 1,75$ (giờ).
Vậy, thời gian là 1,75 giờ.
Cột 4: $s = 81$ km, $v = 36$ km/giờ.
Thời gian $t = 81 : 36$ .
Thực hiện phép chia: $81 div 36 = 2,25$ (giờ).
Vậy, thời gian là 2,25 giờ.

Mẹo kiểm tra: Sau khi tính được thời gian, ta có thể nhân ngược thời gian đó với vận tốc để xem có ra đúng quãng đường ban đầu không. Ví dụ, với cột 1: $2,5 \times 14 = 35$ km, đúng.

Lỗi hay gặp: Học sinh có thể nhầm lẫn công thức hoặc thực hiện phép chia sai, dẫn đến kết quả không chính xác. Chú ý sử dụng máy tính bỏ túi để kiểm tra lại phép tính nếu cần.

Bài 2: Tính thời gian đi/chạy

Bài tập này áp dụng trực tiếp công thức $t = s : v$ và yêu cầu đổi đơn vị thời gian.

a) Thời gian người đi xe đạp:

Quãng đường $s = 23,1$ km.
Vận tốc $v = 13,2$ km/giờ.
Đơn vị của quãng đường và vận tốc đã tương ứng (km và km/giờ), nên thời gian tính ra sẽ có đơn vị là giờ.
Thời gian $t = s : v = 23,1 : 13,2$
Thực hiện phép chia: $23,1 div 13,2 = 1,75$ (giờ).
Đổi đơn vị: 1,75 giờ bao gồm 1 giờ nguyên và 0,75 giờ lẻ.
Để đổi 0,75 giờ ra phút, ta nhân với 60:
$0,75 \times 60 = 45$ (phút).
Vậy, 1,75 giờ = 1 giờ 45 phút.

b) Thời gian người chạy bộ:

Quãng đường $s = 2,5$ km.
Vận tốc $v = 10$ km/giờ.
Đơn vị đã tương ứng.
Thời gian $t = s : v = 2,5 : 10$
Thực hiện phép chia: $2,5 div 10 = 0,25$ (giờ).
Đổi đơn vị: 0,25 giờ bao gồm 0 giờ nguyên và 0,25 giờ lẻ.
Để đổi 0,25 giờ ra phút, ta nhân với 60:
$0,25 \times 60 = 15$ (phút).
Vậy, 0,25 giờ = 15 phút.

Đáp số: a) 1 giờ 45 phút; b) 15 phút.

Mẹo kiểm tra:

Kiểm tra phép chia để ra số giờ.
Kiểm tra phép đổi đơn vị: 1 giờ = 60 phút. Nhân phần thập phân của giờ với 60 để ra số phút.

Lỗi hay gặp:

Nhầm lẫn công thức tính thời gian.
Thực hiện phép chia sai.
Đổi đơn vị thời gian không chính xác (ví dụ: 0,75 giờ bị nhầm thành 75 phút).

Bài 3: Tính thời điểm đến

Bài toán này kết hợp cả việc tính thời gian bay và cộng thời gian khởi hành.

Các bước thực hiện:

Tính thời gian máy bay bay:
- Quãng đường $s = 2150$ km.
- Vận tốc $v = 860$ km/giờ.
- Đơn vị đã tương ứng.
- Thời gian bay $t = s : v = 2150 : 860$
  Thực hiện phép chia: $2150 div 860 = 2,5$ (giờ).
Đổi đơn vị thời gian bay:
- 2,5 giờ = 2 giờ + 0,5 giờ.
- Đổi 0,5 giờ ra phút: $0,5 \times 60 = 30$ (phút).
- Vậy, thời gian bay là 2 giờ 30 phút.
Tính thời điểm đến:
- Thời điểm khởi hành: 8 giờ 45 phút.
- Thời gian bay: 2 giờ 30 phút.
- Thời điểm đến = Thời điểm khởi hành + Thời gian bay
- Ta cộng từng phần:
  Giờ: $8$ giờ + $2$ giờ = $10$ giờ.
  Phút: $45$ phút + $30$ phút = $75$ phút.
- Vì 75 phút lớn hơn 60 phút, ta cần đổi 75 phút thành giờ và phút:
  75 phút = 60 phút + 15 phút = 1 giờ 15 phút.
- Vậy, ta có: 10 giờ + 1 giờ 15 phút = 11 giờ 15 phút.

Đáp số: 11 giờ 15 phút.

Mẹo kiểm tra:

Phép chia quãng đường cho vận tốc cho ra số giờ chính xác.
Phép cộng thời điểm được thực hiện đúng, đặc biệt là việc đổi đơn vị phút sang giờ khi vượt quá 60 phút.

Lỗi hay gặp:

Tính sai thời gian bay.
Khi cộng thời gian, quên đổi 75 phút thành 1 giờ 15 phút, dẫn đến kết quả sai giờ (ví dụ: 10 giờ 75 phút).

Đáp Án/Kết Quả

Tổng kết lại, các bài tập trên trang 143 trang bị cho học sinh kỹ năng giải toán về thời gian trong chuyển động đều.

Bài 1 yêu cầu điền vào bảng, củng cố trực tiếp công thức $t = s : v$ .
Bài 2 yêu cầu tính thời gian và đổi đơn vị, áp dụng $t = s : v$ và quy đổi giờ sang giờ phút.
Bài 3 yêu cầu tính thời điểm đến, kết hợp công thức $t = s : v$ và phép cộng thời điểm.

Các kết quả cuối cùng cho từng bài tập đã được trình bày chi tiết ở trên.

Kết Luận

Chủ đề “Thời gian” trong Toán lớp 5, đặc biệt là các bài tập tại trang 143, là một phần kiến thức quan trọng giúp học sinh phát triển tư duy logic và kỹ năng giải quyết vấn đề. Bằng việc nắm vững công thức cơ bản $t = s : v$ và các quy tắc đổi đơn vị thời gian, học sinh có thể tự tin chinh phục các dạng bài tập liên quan. Việc luyện tập thường xuyên với các bài tập tương tự sẽ giúp các em ghi nhớ kiến thức sâu hơn và áp dụng hiệu quả vào các tình huống thực tế. Bài viết này hy vọng đã mang lại những hướng dẫn bổ ích để giải toán lớp 5 trang 143 một cách dễ dàng và chính xác.

Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.