Định Lý Sin Trong Tam Giác: Công Thức Và Ứng Dụng Chi Tiết

by Thầy Đông · January 7, 2026

Rate this post

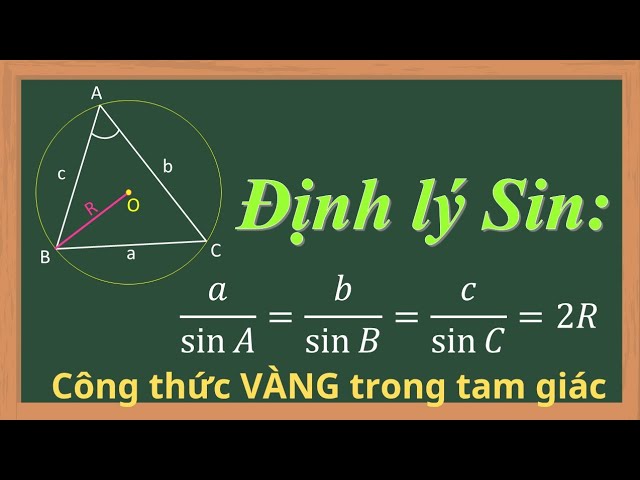
Khi nghiên cứu về các mối quan hệ giữa cạnh và góc trong tam giác, định lý Sin nổi lên như một công cụ toán học vô cùng hữu ích. Đây là một phần kiến thức nền tảng quan trọng, không chỉ giúp giải quyết các bài toán hình học phẳng mà còn có ứng dụng sâu rộng trong nhiều lĩnh vực khoa học kỹ thuật. Bài viết này sẽ đi sâu vào định lý Sin, làm rõ công thức, các dạng bài tập điển hình và cách áp dụng hiệu quả.

Đề Bài

Định lý Sin là một trong những công cụ quan trọng trong hình học, đặc biệt là trong việc giải quyết các bài toán liên quan đến tam giác vuông. Dưới đây là các công thức và ứng dụng của định lý Sin.

Công thức của định lý Sin

Định lý Sin trong tam giác vuông được định nghĩa như sau:

\sin (theta) = \frac{\text{Cạnh đối}}{\text{Cạnh huyền}}

Trong đó:

theta là góc nhọn trong tam giác vuông.
Cạnh đối là cạnh đối diện với góc theta.
Cạnh huyền là cạnh dài nhất của tam giác vuông.

Ứng dụng của định lý Sin

Định lý Sin được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau như toán học, vật lý và kỹ thuật. Dưới đây là một số ứng dụng cụ thể:

1. Tính chiều dài cạnh trong tam giác vuông

Nếu biết góc và độ dài của một cạnh, ta có thể sử dụng định lý Sin để tính chiều dài của cạnh còn lại:

Ví dụ, trong một tam giác vuông với góc theta và cạnh huyền c:

a = c \cdot \sin (theta)

Trong đó a là chiều dài cạnh đối diện với góc theta.

2. Tính góc trong tam giác vuông

Nếu biết độ dài của hai cạnh, ta có thể sử dụng định lý Sin để tính góc trong tam giác vuông:

Ví dụ, trong một tam giác vuông với cạnh đối a và cạnh huyền c:

theta = arcsinleft(\frac{a}{c}\right)

3. Ứng dụng trong vật lý và kỹ thuật

Xác định các lực trong cơ học.
Tính toán các thành phần sóng trong điện tử.
Xác định vị trí trong hệ thống định vị toàn cầu (GPS).

Bảng tóm tắt các ứng dụng của định lý Sin

Ứng dụng	Ví dụ
Tính chiều dài cạnh	$a = c \cdot \sin (theta)$
Tính góc	$theta = arcsinleft(\frac{a}{c}\right)$
Ứng dụng trong vật lý và kỹ thuật	Xác định các lực, tính toán sóng, định vị GPS

Phân Tích Yêu Cầu

Dựa trên đề bài được cung cấp, yêu cầu chính là hiểu và áp dụng Định lý Sin trong tam giác, đặc biệt là tam giác vuông. Các dữ kiện quan trọng bao gồm: công thức cơ bản của định lý Sin liên hệ góc và các cạnh, cũng như các trường hợp ứng dụng cụ thể để tính toán độ dài cạnh hoặc xác định giá trị góc khi biết các yếu tố khác. Hướng giải tổng quát là nhận diện tam giác vuông, xác định các yếu tố đã biết (góc, cạnh) và áp dụng đúng công thức định lý Sin hoặc các hàm lượng giác cơ bản.

Kiến Thức/Nền Tảng Cần Dùng

Để giải quyết các bài toán liên quan đến Định lý Sin, chúng ta cần nắm vững các kiến thức sau:

Định nghĩa các cạnh trong tam giác vuông: Cạnh đối, cạnh kề và cạnh huyền tương ứng với một góc nhọn.
Các hàm lượng giác cơ bản:
- Sinus (sin): Tỷ lệ giữa cạnh đối và cạnh huyền.
  $\sin (theta) = \frac{\text{Cạnh đối}}{\text{Cạnh huyền}}$
- Cosinus (cos): Tỷ lệ giữa cạnh kề và cạnh huyền.
  $\cos (theta) = \frac{\text{Cạnh kề}}{\text{Cạnh huyền}}$
- Tang (tan): Tỷ lệ giữa cạnh đối và cạnh kề.
  $\tan (theta) = \frac{\text{Cạnh đối}}{\text{Cạnh kề}}$
Hàm lượng giác ngược: Arc Sin (arcsin), Arc Cos (arccos), Arc Tan (arctan) được sử dụng để tìm giá trị góc khi biết tỷ lệ của các cạnh.
$theta = arcsinleft(\frac{\text{Cạnh đối}}{\text{Cạnh huyền}}\right)$

Mẹo kiểm tra: Luôn đảm bảo rằng giá trị của sin, cos, tan nằm trong khoảng cho phép ([[-1, 1]] cho sin và cos, không giới hạn cho tan) và giá trị tính toán của góc là hợp lý với hình vẽ (nếu có).

Lỗi hay gặp: Nhầm lẫn giữa cạnh đối, cạnh kề và cạnh huyền; sử dụng sai hàm lượng giác hoặc hàm ngược; lỗi nhập liệu khi tính toán trên máy tính bỏ túi.

Hướng Dẫn Giải Chi Tiết

Định lý Sin, đặc biệt khi áp dụng trong tam giác vuông, là nền tảng cho nhiều bài toán hình học và ứng dụng thực tế. Dưới đây là các bước chi tiết để áp dụng định lý này.

1. Tính chiều dài cạnh khi biết góc và cạnh huyền

Yêu cầu: Tính cạnh đối a của một góc nhọn theta trong tam giác vuông, khi biết độ dài cạnh huyền c.

Các bước thực hiện:

Xác định yếu tố đã cho: Góc nhọn theta, cạnh huyền c.
Xác định yếu tố cần tìm: Cạnh đối a của góc theta.
Chọn công thức phù hợp: Công thức định lý Sin liên hệ góc, cạnh đối và cạnh huyền là:
$\sin (theta) = \frac{a}{c}$
Biến đổi công thức để tìm cạnh cần tìm: Nhân cả hai vế với c, ta được:
$a = c \cdot \sin (theta)$
Thay số và tính toán: Thay giá trị của c và theta vào công thức để tính ra a.

Ví dụ: Cho một tam giác vuông ABC vuông tại A, có cạnh huyền BC = 10 cm và góc angle C = 30^circ. Tính chiều dài cạnh AB (cạnh đối của góc C).

Ta có: c = BC = 10 cm, theta = angle C = 30^circ. Cần tìm a = AB.
Áp dụng công thức: a = c cdot sin(theta)
Thay số: a = 10 cdot sin(30^circ)
Tính toán: sin(30^circ) = 0.5, vậy a = 10 cdot 0.5 = 5 cm.
Kết quả: Chiều dài cạnh AB là 5 cm.

Mẹo kiểm tra: Cạnh đối luôn nhỏ hơn cạnh huyền trong tam giác vuông. Giá trị sin(theta) luôn nhỏ hơn hoặc bằng 1.

Lỗi hay gặp: Sử dụng nhầm cạnh đối với cạnh kề hoặc cạnh huyền; nhập sai giá trị góc hoặc hàm sin trên máy tính.

2. Tính góc khi biết cạnh đối và cạnh huyền

Yêu cầu: Tìm giá trị góc nhọn theta trong tam giác vuông, khi biết độ dài cạnh đối a và cạnh huyền c.

Các bước thực hiện:

Xác định yếu tố đã cho: Cạnh đối a, cạnh huyền c.
Xác định yếu tố cần tìm: Góc nhọn theta.
Chọn công thức phù hợp: Từ định lý Sin:
$\sin (theta) = \frac{a}{c}$
Sử dụng hàm lượng giác ngược để tìm góc: Lấy arcsin (sin mũ -1) cả hai vế:
$theta = arcsinleft(\frac{a}{c}\right)$
Thay số và tính toán: Thay giá trị của a và c vào công thức, sau đó sử dụng chức năng arcsin (hoặc sin^{-1}) trên máy tính để tìm theta.

Ví dụ: Cho một tam giác vuông ABC vuông tại A, có cạnh đối AB = 7 cm và cạnh huyền BC = 14 cm. Tìm số đo góc angle C.

Ta có: Cạnh đối a = AB = 7 cm, cạnh huyền c = BC = 14 cm. Cần tìm góc theta = angle C.
Áp dụng công thức: theta = arcsinleft(frac{a}{c}right)
Thay số: theta = arcsinleft(frac{7}{14}right) = arcsin(0.5)
Tính toán: Sử dụng máy tính, arcsin(0.5) = 30^circ.
Kết quả: Số đo góc C là 30 độ.

Mẹo kiểm tra: Giá trị a/c phải nằm trong khoảng (0, 1] (vì a là cạnh đối và c là cạnh huyền của góc nhọn). Kết quả góc theta phải là một góc nhọn (nhỏ hơn 90 độ).

Lỗi hay gặp: Nhập sai giá trị cạnh; không chuyển đổi chế độ máy tính sang độ (DEG) hoặc radian (RAD) tùy theo yêu cầu đề bài; nhầm lẫn giữa sin và arcsin.

3. Ứng dụng trong vật lý và kỹ thuật

Định lý Sin và các hàm lượng giác liên quan đóng vai trò cốt lõi trong việc phân tích các đại lượng vật lý có tính chất tuần hoàn hoặc được biểu diễn dưới dạng vector.

Phân tích lực: Khi một vật chịu tác động của nhiều lực, việc phân tích các lực này thành các thành phần theo phương vuông góc thường sử dụng các hàm sin và cos. Định lý Sin có thể được dùng để tìm mối quan hệ giữa các lực và các góc hợp bởi chúng, đặc biệt trong các hệ cân bằng hoặc trong các cấu trúc phức tạp.
Điện tử và sóng: Các tín hiệu điện tử, sóng âm, sóng ánh sáng thường được mô tả bằng các hàm điều hòa như Asin(omega t + phi). Việc phân tích, tổng hợp và xử lý các tín hiệu này dựa trên các phép toán lượng giác. Ví dụ, để tìm thành phần biên độ của một tín hiệu, ta cần sử dụng đến các công thức liên quan đến hàm sin.
Định vị GPS: Hệ thống GPS hoạt động dựa trên nguyên lý đo khoảng cách từ thiết bị nhận đến ít nhất bốn vệ tinh. Việc tính toán vị trí chính xác của thiết bị trên bề mặt trái đất liên quan đến giải một hệ phương trình mà các hàm lượng giác và hình học không gian là không thể thiếu.

Trong các lĩnh vực này, việc nắm vững Định lý Sin giúp các kỹ sư và nhà khoa học có thể xây dựng mô hình toán học chính xác cho các hiện tượng vật lý, từ đó đưa ra giải pháp kỹ thuật hiệu quả.

Đáp Án/Kết Quả

Tính chiều dài cạnh: Nếu biết góc nhọn theta và cạnh huyền c, cạnh đối a được tính bằng a = c cdot sin(theta).
Tính góc: Nếu biết cạnh đối a và cạnh huyền c, góc nhọn theta được tìm bằng theta = arcsinleft(frac{a}{c}right).
Ứng dụng: Định lý Sin là công cụ cơ bản trong vật lý và kỹ thuật để phân tích lực, xử lý tín hiệu sóng và hỗ trợ hệ thống định vị.

Định lý Sin là một nguyên tắc toán học mạnh mẽ, cung cấp phương pháp rõ ràng để liên kết các góc và cạnh trong tam giác, đặc biệt hữu ích trong tam giác vuông. Nắm vững công thức và các ứng dụng thực tế của định lý Sin sẽ trang bị cho người học một công cụ giải toán hiệu quả, mở ra cánh cửa hiểu biết sâu sắc hơn về thế giới xung quanh qua lăng kính toán học.

Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.