Định Lý Pytago Là Gì? Công Thức, Chứng Minh Và Ứng Dụng Thực Tế

Định lý Pytago là một trong những định lý nền tảng và quan trọng bậc nhất trong hình học Euclid, liên quan mật thiết đến các tam giác vuông. Đây là kiến thức cơ bản mà mọi học sinh đều cần nắm vững để giải quyết nhiều bài toán từ đơn giản đến phức tạp.

Đề Bài

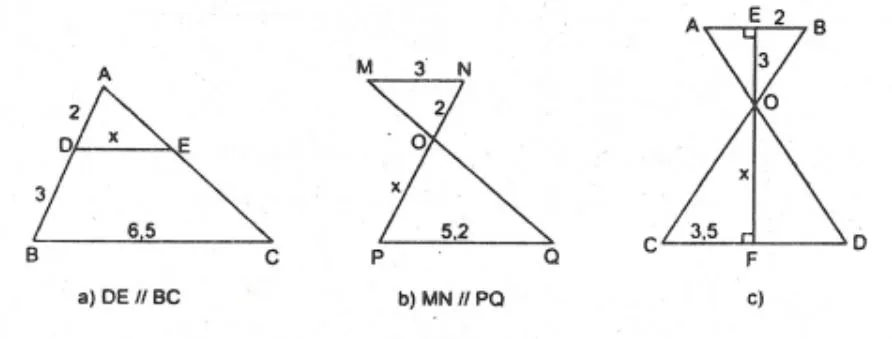
Trong sách giáo khoa Toán 8, bộ Cánh diều, trang 97, định lý Pytago phát biểu như sau: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của 2 cạnh góc vuông.

minh hoa dinh ly pythagore Định lý này được đặt tên theo nhà toán học Hy Lạp Pythagore, mặc dù mối liên hệ giữa bình phương các cạnh của tam giác vuông đã được biết đến từ trước đó trong lịch sử.

Có rất nhiều cách để chứng minh định lý Pytago, bao gồm cả phương pháp hình học và đại số, nhiều cách trong số đó đã xuất hiện từ hàng nghìn năm trước.

Phân Tích Yêu Cầu

Yêu cầu cốt lõi là làm rõ khái niệm định lý Pytago, trình bày công thức toán học của nó dưới dạng thuận và đảo, kèm theo ví dụ minh họa cụ thể. Đồng thời, bài viết cần cung cấp thêm thông tin về lịch sử cũng như các ứng dụng thực tế của định lý.

Kiến Thức/Nền Tảng Cần Dùng

Để hiểu rõ định lý Pytago, chúng ta cần nắm vững các khái niệm cơ bản về tam giác vuông, bao gồm:

• Tam giác vuông: Là tam giác có một góc bằng 90 độ.
• Cạnh huyền: Là cạnh đối diện với góc vuông, là cạnh dài nhất trong tam giác vuông.
• Cạnh góc vuông: Là hai cạnh tạo thành góc vuông.

Định lý Pytago Thuận

Phát biểu: Trong một tam giác vuông, bình phương độ dài cạnh huyền bằng tổng bình phương độ dài hai cạnh góc vuông.

Giả sử ta có một tam giác vuông ABC, vuông tại đỉnh A. Khi đó, AB và AC là hai cạnh góc vuông, còn BC là cạnh huyền. Theo định lý Pytago thuận, ta có công thức:

AB^2 + AC^2 = BC^2

Hoặc, nếu ký hiệu độ dài các cạnh là:

• a, b là độ dài hai cạnh góc vuông.
• c là độ dài cạnh huyền.

Thì công thức trở thành:

a^2 + b^2 = c^2

Định lý Pytago Đảo

Phát biểu: Nếu một tam giác có bình phương độ dài một cạnh bằng tổng bình phương độ dài hai cạnh còn lại, thì tam giác đó là tam giác vuông. Cụ thể, góc đối diện với cạnh có bình phương lớn nhất là góc vuông.

Giả sử ta có một tam giác ABC với độ dài ba cạnh là a, b, c. Nếu thỏa mãn điều kiện:

a^2 + b^2 = c^2

Thì tam giác ABC là tam giác vuông tại đỉnh đối diện với cạnh c (cạnh có độ dài lớn nhất).

Chứng minh Định lý Pytago (Một cách phổ biến)

Có rất nhiều cách chứng minh định lý Pytago, dưới đây là một cách chứng minh bằng phương pháp diện tích, sử dụng hình vuông lớn chứa bốn tam giác vuông giống nhau.

Xét một tam giác vuông có các cạnh góc vuông là a và b, cạnh huyền là c.
Ta xây dựng một hình vuông lớn có cạnh là a + b. Bên trong hình vuông lớn này, ta xếp bốn tam giác vuông có cạnh a và b, cạnh huyền c sao cho chúng tạo thành một hình vuông nhỏ hơn ở giữa với cạnh là c.

minh hoa chung minh dinh ly pythagore

• Diện tích hình vuông lớn: Có cạnh là a + b, nên diện tích là (a + b)^2.
  (a + b)^2 = a^2 + 2ab + b^2

• Diện tích của bốn tam giác vuông: Mỗi tam giác vuông có diện tích là (1/2)ab. Tổng diện tích của bốn tam giác này là 4 (1/2)ab = 2ab.

• Diện tích hình vuông nhỏ ở giữa: Có cạnh là c, nên diện tích là c^2.

Tổng diện tích của bốn tam giác vuông cộng với diện tích hình vuông nhỏ ở giữa phải bằng diện tích hình vuông lớn ban đầu.
Do đó:
2ab + c^2 = (a + b)^2
2ab + c^2 = a^2 + 2ab + b^2

Trừ 2ab khỏi cả hai vế, ta thu được:
c^2 = a^2 + b^2

Đây chính là định lý Pytago thuận.

Hướng Dẫn Giải Chi Tiết

Ví dụ 1: Áp dụng Định lý Pytago Thuận

Đề bài: Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 12 cm. Tính độ dài cạnh BC.

Phân tích: Ta có tam giác ABC vuông tại A, AB và AC là hai cạnh góc vuông, BC là cạnh huyền. Ta cần tìm độ dài cạnh huyền BC.

Các bước giải:

1. Áp dụng định lý Pytago thuận cho tam giác ABC vuông tại A:
   BC^2 = AB^2 + AC^2
2. Thay số liệu đã cho vào công thức:
   BC^2 = 5^2 + 12^2
3. Tính toán các bình phương:
   BC^2 = 25 + 144
4. Tính tổng:
   BC^2 = 169
5. Tìm độ dài BC bằng cách lấy căn bậc hai:
   BC = \sqrt{169}
   BC = 13 (cm)

Kết quả: Độ dài cạnh BC là 13 cm.

Mẹo kiểm tra: Các bộ số (5, 12, 13) tạo thành một bộ ba số Pytago nguyên thủy, thường gặp trong các bài toán. Bạn có thể kiểm tra lại bằng cách lấy 5^2 + 12^2 có bằng 13^2 không.

Lỗi hay gặp: Học sinh có thể nhầm lẫn cạnh huyền với cạnh góc vuông, hoặc quên bình phương hai cạnh trước khi cộng.

Ví dụ 2: Áp dụng Định lý Pytago Đảo

Đề bài: Cho tam giác DEG có DE = 7 cm, DG = 24 cm và EG = 25 cm. Hỏi tam giác DEG có phải là tam giác vuông không? Nếu có, vuông tại đỉnh nào?

Phân tích: Ta có độ dài ba cạnh của tam giác DEG. Để xác định xem nó có phải tam giác vuông hay không, ta sẽ kiểm tra xem có thỏa mãn hệ thức Pytago đảo hay không. Cần xác định cạnh dài nhất là EG (25 cm), đây có thể là cạnh huyền nếu tam giác vuông.

Các bước giải:

1. Tính bình phương của cạnh dài nhất (EG):
   EG^2 = 25^2
   EG^2 = 625
2. Tính tổng bình phương của hai cạnh còn lại (DE và DG):
   DE^2 + DG^2 = 7^2 + 24^2
   DE^2 + DG^2 = 49 + 576
   DE^2 + DG^2 = 625
3. So sánh kết quả: Ta thấy EG^2 = DE^2 + DG^2 (cùng bằng 625).
4. Kết luận: Theo định lý Pytago đảo, tam giác DEG là tam giác vuông. Vì cạnh EG là cạnh có bình phương bằng tổng bình phương hai cạnh còn lại, nên EG là cạnh huyền. Góc vuông sẽ là góc đối diện với cạnh huyền EG, tức là góc D.

Kết quả: Tam giác DEG là tam giác vuông tại đỉnh D.

Mẹo kiểm tra: Các bộ số (7, 24, 25) cũng là một bộ ba số Pytago nguyên thủy.

Lỗi hay gặp: Quên kiểm tra bình phương của cạnh dài nhất hoặc nhầm lẫn thứ tự các cạnh.

Ứng Dụng Thực Tế của Định lý Pytago

Định lý Pytago không chỉ là một khái niệm trừu tượng trong sách vở mà còn có vô số ứng dụng thực tế trong cuộc sống, kỹ thuật và khoa học:

• Xây dựng và Kiến trúc: Thợ mộc, thợ xây thường dùng định lý này để kiểm tra xem một góc có thực sự vuông hay không (ví dụ: kiểm tra góc tường, góc khung cửa). Họ có thể đo theo tỉ lệ 3-4-5 đơn vị (ví dụ: 3m, 4m, 5m) để đảm bảo góc vuông.
• Thiết kế và Định vị: Khi tính toán khoảng cách giữa hai điểm trên bản đồ, trên mặt phẳng tọa độ, hoặc trong hệ thống GPS, định lý Pytago là công cụ cơ bản. Ví dụ, nếu bạn biết tọa độ X và Y của hai địa điểm, bạn có thể tính khoảng cách đường chim bay giữa chúng.
• Kỹ thuật Cơ khí: Trong việc thiết kế các bộ phận máy móc, tính toán lực căng, độ dài cần thiết, hoặc khoảng cách trong các cấu trúc cơ khí phức tạp, định lý Pytago đóng vai trò quan trọng.
• Đo đạc địa lý: Các nhà trắc địa sử dụng định lý này để tính toán chiều cao, khoảng cách, diện tích, hoặc vẽ bản đồ chính xác hơn.
• Khoa học máy tính: Trong đồ họa máy tính, việc tính toán khoảng cách giữa các điểm ảnh (pixels) hoặc các đối tượng trên màn hình thường dựa vào định lý này.
• Đời sống hàng ngày: Ngay cả trong những việc đơn giản như ước lượng chiều dài đường chéo của màn hình TV, hay tính khoảng cách di chuyển trên mặt đất, chúng ta cũng đang áp dụng nguyên lý của định lý Pytago.

Đáp Án/Kết Quả

Định lý Pytago là một công cụ toán học mạnh mẽ, cho phép chúng ta tính toán các cạnh chưa biết trong một tam giác vuông dựa trên độ dài hai cạnh còn lại. Định lý có hai dạng: thuận (tính cạnh huyền hoặc cạnh góc vuông khi biết hai cạnh còn lại) và đảo (xác định tam giác có vuông hay không). Các bộ ba số nguyên (a, b, c) thỏa mãn a^2 + b^2 = c^2 được gọi là bộ ba số Pytago (ví dụ: 3-4-5, 5-12-13, 7-24-25). Định lý này có ứng dụng rộng rãi từ khoa học, kỹ thuật đến các hoạt động thực tế hàng ngày.

Thông Tin Thú Vị Về Pythagore

Pythagoras (khoảng 570 TCN – 495 TCN) là một nhà toán học và triết gia Hy Lạp cổ đại. Ông có niềm tin sâu sắc vào sức mạnh của các con số, cho rằng mọi thứ trong vũ trụ đều có thể giải thích bằng số học. Pythagoras còn được ghi nhận là người phát hiện ra mối liên hệ giữa âm nhạc và toán học. Ông nhận thấy rằng các âm thanh hài hòa có thể được biểu diễn bằng các tỉ lệ số học đơn giản của độ dài dây đàn. Ví dụ, dây đàn có độ dài tỉ lệ 2:1 sẽ tạo ra quãng tám, còn tỉ lệ 3:2 tạo ra quãng năm. Sự khám phá này đã đặt nền móng cho lý thuyết nhạc phương Tây.

Hiện nay, không còn bất kỳ tác phẩm gốc nào của Pythagoras được lưu giữ. Những kiến thức chúng ta có về ông chủ yếu đến từ các ghi chép của học trò và các triết gia sau này, như Aristotle. Do đó, tiểu sử của ông thường pha trộn giữa huyền thoại và thực tế lịch sử.

Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông