Giải Toán 8 Tập 2 Trang 87: Tam Giác Đồng Dạng
Chào mừng bạn đến với bài viết chi tiết về cách giải các bài tập liên quan đến tam giác đồng dạng trong chương trình Toán 8, tập 2, trang 87. Bài viết này sẽ cung cấp cho bạn kiến thức nền tảng, phương pháp giải từng bước và các mẹo hữu ích để nắm vững chủ đề quan trọng này. Chúng ta sẽ cùng nhau khám phá các định lý, cách nhận biết và áp dụng tam giác đồng dạng vào giải quyết các bài toán thực tế.
Đề Bài
Cho hai tam giác ABC và A’B’C’ có độ dài các cạnh (theo đơn vị cm) như Hình 9.15. Biết rằng (widehat A = widehat {A’} = 60^0)
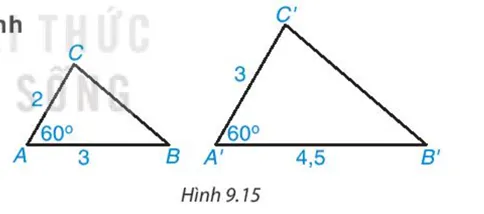
– So sánh các tỉ số (frac{{A’B’}}{{AB}}{;^{}}frac{{A’C’}}{{AC}})
– Dùng thước có vạch chia đo độ dài BC, B’C’ và tính tỉ số ( frac {B′C′} {BC} )
– Theo em, tam giác A’B’C’ có đồng dạng với tam giác ABC không? Nếu có thì tỉ số đồng dạng là bao nhiêu?
Các cặp tam giác nào trong hình 9.17 là đồng dạng? (Các kích thước được tính theo đơn vị centimét). Viết đúng kí hiệu đồng dạng.
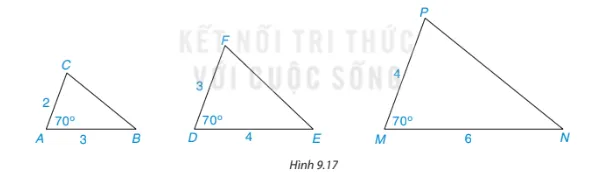
Cho ΔA’B’C’ ∽ ΔABC. Trên tia đối của các tia CB, C’B’ lần lượt lấy các điểm M, M’ sao cho (frac{{MC}}{{MB}} = frac{{M’C’}}{{M’B’}}). Chứng minh rằng ΔA’B’M’ ∽ ΔABM
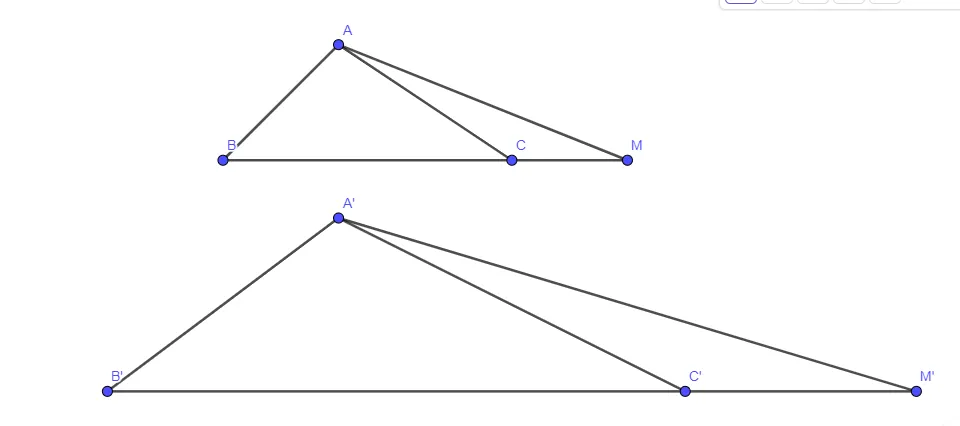
Bạn Lan nhận xét rằng nếu tam giác ABC và tam giác A’B’C’ có (frac{{A’B’}}{{AB}} = frac{{A’C’}}{{AC}}) và (widehat {B’} = widehat B) thì chúng đồng dạng. Theo em bạn Lan nhận xét đúng không vì sao?
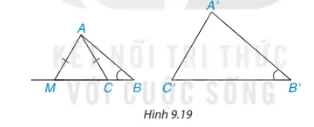
Gợi ý. Khi góc ACB tù, lấy điểm M trên tia BC sao cho ( Delta AMC ) cân (H.9.19) rồi xét xem trong hai tam giác ABC và ABM, tam giác nào đồng dạng với tam giác A’B’C’.
Phân Tích Yêu Cầu
Các bài tập trên yêu cầu chúng ta xác định sự đồng dạng giữa các tam giác dựa trên các tỉ lệ cạnh và góc đã cho. Cụ thể, chúng ta cần:
- Tính toán và so sánh các tỉ lệ độ dài cạnh.
- Áp dụng các trường hợp nhận biết tam giác đồng dạng (cạnh-cạnh-cạnh, cạnh-góc-cạnh, góc-góc).
- Chứng minh sự đồng dạng của các tam giác trong các tình huống hình học phức tạp hơn.
- Đánh giá tính đúng đắn của một nhận xét về trường hợp đồng dạng tam giác.
Kiến Thức/Nền Tảng Cần Dùng
Để giải quyết các bài toán về tam giác đồng dạng, chúng ta cần nắm vững các định lý sau:
1. Định nghĩa hai tam giác đồng dạng
Hai tam giác được gọi là đồng dạng với nhau nếu chúng có ba cặp góc tương ứng bằng nhau và ba cặp cạnh tương ứng tỉ lệ.
Nếu (Delta ABC sim Delta A’B’C’) thì (widehat A = widehat {A’}, widehat B = widehat {B’}, widehat C = widehat {C’}) và (frac{{A’B’}}{{AB}} = frac{{B’C’}}{{BC}} = frac{{C’A’}}{{CA}} = k). Tỉ số (k) được gọi là tỉ số đồng dạng.
2. Các trường hợp nhận biết tam giác đồng dạng
Trường hợp 1: Góc – Góc (GG)
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia, thì hai tam giác đó đồng dạng.
Nếu (widehat A = widehat {A’}) và (widehat B = widehat {B’}) thì (Delta ABC sim Delta A’B’C’).Trường hợp 2: Cạnh – Góc – Cạnh (CGC)
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc xen giữa hai cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
Nếu (frac{{AB}}{{A’B’}} = frac{{AC}}{{A’C’}}) và (widehat A = widehat {A’}) thì (Delta ABC sim Delta A’B’C’).Trường hợp 3: Cạnh – Cạnh – Cạnh (CCC)
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia, thì hai tam giác đó đồng dạng.
Nếu (frac{{AB}}{{A’B’}} = frac{{BC}}{{B’C’}} = frac{{CA}}{{C’A’}}) thì (Delta ABC sim Delta A’B’C’).
Hướng Dẫn Giải Chi Tiết
Bài tập 1 (Hình 9.15)
Đề bài: Cho hai tam giác ABC và A’B’C’ có độ dài các cạnh (theo đơn vị cm) như Hình 9.15. Biết rằng (widehat A = widehat {A’} = 60^0)
– So sánh các tỉ số (frac{{A’B’}}{{AB}}{;^{}}frac{{A’C’}}{{AC}})
– Dùng thước có vạch chia đo độ dài BC, B’C’ và tính tỉ số ( frac {B′C′} {BC} )
– Theo em, tam giác A’B’C’ có đồng dạng với tam giác ABC không? Nếu có thì tỉ số đồng dạng là bao nhiêu?
Phân Tích Yêu Cầu: Bài toán cho hai tam giác, biết một cặp góc bằng nhau và độ dài các cạnh. Yêu cầu so sánh tỉ lệ các cạnh và xác định sự đồng dạng.
Kiến Thức Cần Dùng: Trường hợp đồng dạng Cạnh – Góc – Cạnh (CGC) và Góc – Góc (GG).
Hướng Dẫn Giải Chi Tiết:
Quan sát Hình 9.15, ta có các độ dài cạnh như sau:
AB = 4 cm, AC = 5 cm, BC = 6 cm
A’B’ = 6 cm, A’C’ = 7.5 cm, B’C’ = 9 cm
Bước 1: So sánh các tỉ số cạnh.
Ta tính tỉ số (frac{{A’B’}}{{AB}} = frac{6}{4} = frac{3}{2}).
Ta tính tỉ số (frac{{A’C’}}{{AC}} = frac{7.5}{5} = frac{15/2}{5} = frac{15}{10} = frac{3}{2}).
Vậy, ta có (frac{{A’B’}}{{AB}} = frac{{A’C’}}{{AC}} = frac{3}{2}).Bước 2: Đo và tính tỉ số cạnh BC và B’C’.
Sử dụng thước đo, ta xác định độ dài BC = 6 cm và B’C’ = 9 cm.
Ta tính tỉ số (frac{{B’C’}}{{BC}} = frac{9}{6} = frac{3}{2}).Bước 3: Xác định sự đồng dạng.
Ta có (widehat A = widehat {A’} = 60^0) (theo giả thiết).
Ta đã chứng minh được (frac{{A’B’}}{{AB}} = frac{{A’C’}}{{AC}} = frac{3}{2}).
Áp dụng trường hợp đồng dạng Cạnh – Góc – Cạnh (CGC), ta kết luận:
(Delta A’B’C’ sim Delta ABC).
Tỉ số đồng dạng là (k = frac{3}{2}).
Mẹo kiểm tra: Sau khi xác định được tỉ số đồng dạng, hãy kiểm tra lại xem các cạnh còn lại có tuân theo tỉ lệ đó không. Ở đây, tỉ lệ (frac{{B’C’}}{{BC}} = frac{3}{2}) cũng khớp, khẳng định kết quả đúng.
Lỗi hay gặp: Quên không ghi rõ tỉ số đồng dạng hoặc nhầm lẫn thứ tự các đỉnh khi viết kí hiệu đồng dạng.
Bài tập 2 (Hình 9.17)
Đề bài: Những cặp tam giác nào trong hình 9.17 là đồng dạng? (Các kích thước được tính theo đơn vị centimét). Viết đúng kí hiệu đồng dạng.
Phân Tích Yêu Cầu: Bài toán yêu cầu nhận diện các cặp tam giác đồng dạng từ một hình vẽ cho trước, dựa vào tỉ lệ các cạnh và góc.
Kiến Thức Cần Dùng: Trường hợp đồng dạng Cạnh – Góc – Cạnh (CGC) và Cạnh – Cạnh – Cạnh (CCC).
Hướng Dẫn Giải Chi Tiết:
Quan sát Hình 9.17, ta có các tam giác với các độ dài cạnh như sau:
Tam giác ABC: AB = 3, BC = 4, AC = 5
Tam giác MNP: MN = 6, NP = 8, MP = 10
Tam giác DEF: DE = 3, EF = 4, DF = 5
Tam giác PQR: PQ = 3, QR = 4, PR = 5
Xét tam giác ABC và tam giác DEF:
Ta có AB = DE = 3, BC = EF = 4, AC = DF = 5.
Ba cặp cạnh tương ứng bằng nhau, nên (Delta ABC = Delta DEF) (c.c.c). Do đó, chúng cũng đồng dạng.
(Delta ABC sim Delta DEF) với tỉ số đồng dạng là 1.Xét tam giác ABC và tam giác PQR:
Ta có AB = PQ = 3, BC = QR = 4, AC = PR = 5.
Ba cặp cạnh tương ứng bằng nhau, nên (Delta ABC = Delta PQR) (c.c.c). Do đó, chúng cũng đồng dạng.
(Delta ABC sim Delta PQR) với tỉ số đồng dạng là 1.Xét tam giác ABC và tam giác MNP:
Ta có tỉ lệ các cạnh:
(frac{{MN}}{{AB}} = frac{6}{3} = 2)
(frac{{NP}}{{BC}} = frac{8}{4} = 2)
(frac{{MP}}{{AC}} = frac{10}{5} = 2)
Ba cặp cạnh tương ứng tỉ lệ với cùng tỉ số 2. Áp dụng trường hợp đồng dạng Cạnh – Cạnh – Cạnh (CCC), ta có:
(Delta MNP sim Delta ABC) với tỉ số đồng dạng là 2.Các cặp tam giác đồng dạng khác:
Tương tự, ta có thể so sánh các cặp tam giác còn lại. Ví dụ:
(Delta DEF sim Delta PQR) (vì chúng bằng nhau).
(Delta MNP sim Delta DEF) (vì (frac{{MN}}{{DE}} = frac{6}{3} = 2), (frac{{NP}}{{EF}} = frac{8}{4} = 2), (frac{{MP}}{{DF}} = frac{10}{5} = 2)).
(Delta MNP sim Delta PQR) (tương tự).
Các cặp tam giác đồng dạng là:
(Delta ABC sim Delta DEF)
(Delta ABC sim Delta PQR)
(Delta ABC sim Delta MNP) (với tỉ số 1/2)
(Delta DEF sim Delta PQR)
(Delta DEF sim Delta MNP) (với tỉ số 1/2)
(Delta PQR sim Delta MNP) (với tỉ số 1/2)
Lưu ý: Khi viết kí hiệu đồng dạng, cần đảm bảo thứ tự các đỉnh tương ứng. Ví dụ, nếu (Delta ABC sim Delta MNP) thì A tương ứng với M, B tương ứng với N, C tương ứng với P.
Bài tập 3 (Hình 9.15 – Chứng minh đồng dạng)
Đề bài: Cho ΔA’B’C’ ∽ ΔABC. Trên tia đối của các tia CB, C’B’ lần lượt lấy các điểm M, M’ sao cho (frac{{MC}}{{MB}} = frac{{M’C’}}{{M’B’}}). Chứng minh rằng ΔA’B’M’ ∽ ΔABM
Phân Tích Yêu Cầu: Bài toán yêu cầu chứng minh sự đồng dạng của hai tam giác mới (ΔA’B’M’ và ΔABM) dựa trên giả thiết ban đầu (ΔA’B’C’ ∽ ΔABC) và một tỉ lệ đoạn thẳng liên quan đến các điểm M, M’.
Kiến Thức Cần Dùng: Định nghĩa và các trường hợp nhận biết tam giác đồng dạng, tính chất tỉ lệ thức.
Hướng Dẫn Giải Chi Tiết:
Ta có các giả thiết:
- (Delta A’B’C’ sim Delta ABC)
- M thuộc tia đối của tia CB, M’ thuộc tia đối của tia C’B’.
- (frac{{MC}}{{MB}} = frac{{M’C’}}{{M’B’}}).
Chứng minh:
Vì M thuộc tia đối của tia CB, nên C nằm giữa M và B. Do đó, MB = MC + CB.
Tương tự, vì M’ thuộc tia đối của tia C’B’, nên C’ nằm giữa M’ và B’. Do đó, M’B’ = M’C’ + C’B’.
Từ giả thiết (frac{{MC}}{{MB}} = frac{{M’C’}}{{M’B’}}), ta thay MB và M’B’:
(frac{{MC}}{{MC + CB}} = frac{{M’C’}}{{M’C’ + C’B’}}).
Chia cả tử và mẫu của mỗi vế cho MC và M’C’ (giả sử MC, M’C’ khác 0):
(frac{1}{{frac{{MC}}{{MC}} + frac{{CB}}{{MC}}}} = frac{1}{{frac{{M’C’}}{{M’C’}} + frac{{C’B’}}{{M’C’}}}})
(frac{1}{{1 + frac{{CB}}{{MC}}}} = frac{1}{{1 + frac{{C’B’}}{{M’C’}}}})
(1 + frac{{CB}}{{MC}} = 1 + frac{{C’B’}}{{M’C’}})
(frac{{CB}}{{MC}} = frac{{C’B’}}{{M’C’}}).
Từ đó suy ra: (frac{{MC}}{{CB}} = frac{{M’C’}}{{C’B’}}).
Cộng 1 vào hai vế: (frac{{MC}}{{CB}} + 1 = frac{{M’C’}}{{C’B’}} + 1)
(frac{{MC + CB}}{{CB}} = frac{{M’C’ + C’B’}}{{C’B’}})
(frac{{MB}}{{CB}} = frac{{M’B’}}{{C’B’}}).
Suy ra tỉ lệ nghịch đảo: (frac{{M’B’}}{{MB}} = frac{{C’B’}}{{CB}} ) (1).
Vì (Delta A’B’C’ sim Delta ABC) (theo giả thiết), ta có:
(widehat {B’} = widehat B)
(frac{{A’B’}}{{AB}} = frac{{B’C’}}{{BC}} = frac{{C’A’}}{{CA}} = k) (với k là tỉ số đồng dạng).
Từ đó, ta có (frac{{A’B’}}{{AB}} = frac{{B’C’}}{{BC}}).
Kết hợp (1) và tỉ lệ trên:
(frac{{M’B’}}{{MB}} = frac{{C’B’}}{{CB}} = frac{{A’B’}}{{AB}}).
Ta có (frac{{M’B’}}{{MB}} = frac{{A’B’}}{{AB}}).
Xét hai tam giác (Delta A’B’M’) và (Delta ABM):
Ta có (widehat {B’} = widehat B) (chứng minh trên).
Ta có (frac{{A’B’}}{{AB}} = frac{{M’B’}}{{MB}}).
Áp dụng trường hợp đồng dạng Cạnh – Góc – Cạnh (CGC), ta kết luận:
(Delta A’B’M’ sim Delta ABM).
Mẹo kiểm tra: Đảm bảo rằng các tỉ lệ đoạn thẳng được thiết lập đúng, đặc biệt là khi M, M’ nằm trên tia đối.
Lỗi hay gặp: Nhầm lẫn giữa đoạn thẳng và tỉ lệ, hoặc không xử lý đúng các điểm nằm trên tia đối.
Bài tập 4 (Nhận xét của Lan)
Đề bài: Bạn Lan nhận xét rằng nếu tam giác ABC và tam giác A’B’C’ có (frac{{A’B’}}{{AB}} = frac{{A’C’}}{{AC}}) và (widehat {B’} = widehat B) thì chúng đồng dạng. Theo em bạn Lan nhận xét đúng không vì sao?
Phân Tích Yêu Cầu: Đánh giá tính đúng đắn của một nhận xét về trường hợp đồng dạng tam giác. Nhận xét này có vẻ giống trường hợp Cạnh – Góc – Cạnh nhưng lại sử dụng góc (widehat {B’}) thay vì góc xen giữa hai cạnh đã cho tỉ lệ.
Kiến Thức Cần Dùng: Các trường hợp nhận biết tam giác đồng dạng (GG, CGC, CCC), đặc biệt là trường hợp CGC.
Hướng Dẫn Giải Chi Tiết:
Nhận xét của bạn Lan là: Nếu (frac{{A’B’}}{{AB}} = frac{{A’C’}}{{AC}}) và (widehat {B’} = widehat B) thì (Delta A’B’C’ sim Delta ABC).
Để kiểm tra tính đúng đắn, chúng ta hãy xem xét các trường hợp đồng dạng đã học:
- Trường hợp GG: Cần hai cặp góc bằng nhau. Ta chỉ có (widehat {B’} = widehat B).
- Trường hợp CGC: Cần hai cặp cạnh tỉ lệ VÀ góc xen giữa hai cặp cạnh đó bằng nhau. Ở đây, ta có (frac{{A’B’}}{{AB}} = frac{{A’C’}}{{AC}}), nhưng góc xen giữa hai cạnh này trong (Delta A’B’C’) là (widehat {A’}) và trong (Delta ABC) là (widehat A). Nhận xét của Lan lại sử dụng (widehat {B’}) và (widehat B), là các góc KHÔNG xen giữa hai cặp cạnh đã cho tỉ lệ.
- Trường hợp CCC: Cần ba cặp cạnh tỉ lệ.
Xét một ví dụ phản chứng:
Giả sử ta có (Delta ABC) với các cạnh AB = 3, AC = 4, (widehat B = 30^0).
Và (Delta A’B’C’) với A’B’ = 6, A’C’ = 8, (widehat {B’} = 30^0).
Ta có (frac{{A’B’}}{{AB}} = frac{6}{3} = 2) và (frac{{A’C’}}{{AC}} = frac{8}{4} = 2).
Và (widehat {B’} = widehat B = 30^0).
Theo nhận xét của Lan, (Delta A’B’C’ sim Delta ABC).
Tuy nhiên, ta có thể xây dựng một tam giác (Delta A’B’C’) khác với (widehat {A’} ne widehat A).
Ví dụ, xét (Delta ABC) với AB=3, AC=4, (widehat A = 90^0). Khi đó BC = 5.
Xét (Delta A’B’C’) với A’B’=6, A’C’=8. Tỉ lệ (frac{{A’B’}}{{AB}} = frac{6}{3} = 2) và (frac{{A’C’}}{{AC}} = frac{8}{4} = 2).
Nếu (widehat {A’} = 90^0), thì (Delta A’B’C’ sim Delta ABC) theo trường hợp CGC.
Nhưng nếu ta chọn (widehat {A’} ne 90^0) sao cho (widehat {B’} = widehat B) (điều này có thể xảy ra, ví dụ dùng định lý sin), thì hai tam giác có thể không đồng dạng.
Cụ thể hơn, trường hợp Lan đưa ra giống với trường hợp nhận biết tam giác bằng nhau Cạnh – Góc – Cạnh (CAC) nhưng lại áp dụng cho sự đồng dạng và sử dụng góc không xen giữa. Trường hợp đồng dạng CGC yêu cầu góc xen giữa hai cạnh tỉ lệ phải bằng nhau.
Kết luận: Nhận xét của bạn Lan không chính xác.
Lý do: Trường hợp đồng dạng Cạnh – Góc – Cạnh yêu cầu góc xen giữa hai cạnh tỉ lệ phải bằng nhau. Lan đã cho tỉ lệ hai cạnh (frac{{A’B’}}{{AB}} = frac{{A’C’}}{{AC}}) nhưng lại sử dụng góc (widehat {B’} = widehat B) là góc không xen giữa hai cặp cạnh này. Góc (widehat {A’}) và (widehat A) mới là góc xen giữa. Nếu chỉ có (widehat {B’} = widehat B) và tỉ lệ hai cạnh đó thì chưa đủ điều kiện để hai tam giác đồng dạng.
Gợi ý trong bài toán: Khi góc ACB tù, lấy điểm M trên tia BC sao cho ( Delta AMC ) cân (H.9.19). Điều này cho thấy có thể tồn tại các trường hợp mà tỉ lệ cạnh và một góc bằng nhau không dẫn đến đồng dạng nếu góc đó không phải là góc xen giữa.
Mẹo kiểm tra: Luôn nhớ rằng trường hợp CGC cho đồng dạng yêu cầu góc xen giữa hai cạnh tỉ lệ phải bằng nhau.
Đáp Án/Kết Quả
- Bài tập 1: (Delta A’B’C’ sim Delta ABC) với tỉ số đồng dạng (k = frac{3}{2}).
- Bài tập 2: Các cặp tam giác đồng dạng là (Delta ABC sim Delta DEF), (Delta ABC sim Delta PQR), (Delta ABC sim Delta MNP) (tỉ số 1/2), v.v. (xem chi tiết ở phần hướng dẫn).
- Bài tập 3: Đã chứng minh được (Delta A’B’M’ sim Delta ABM).
- Bài tập 4: Nhận xét của bạn Lan không chính xác vì thiếu điều kiện góc xen giữa hai cạnh tỉ lệ phải bằng nhau.
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải các bài tập tam giác đồng dạng trong chương trình Toán 8. Nắm vững các định lý và luyện tập thường xuyên sẽ giúp bạn tự tin chinh phục các dạng bài tập tương tự, đặc biệt là các bài toán trong Giải Toán 8 Tập 2 Trang 87.
Ngày chỉnh sửa nội dung mới nhất January 15, 2026 by Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.













