Giải Toán 8 trang 74 Tập 1 Kết nối tri thức

by Thầy Đông · January 8, 2026

Rate this post

Trang này cung cấp lời giải chi tiết cho Giải Toán 8 trang 74 Tập 1 thuộc bộ sách Kết nối tri thức, giúp học sinh lớp 8 nắm vững kiến thức về các loại tứ giác. Bài viết tập trung vào việc phân tích yêu cầu, cung cấp nền tảng lý thuyết cần thiết và hướng dẫn giải từng bước, đảm bảo tính chính xác và dễ hiểu cho các dạng bài tập cuối chương 3.

Đề Bài

Bài 3.39 trang 74 Toán 8 Tập 1: Trong các khẳng định sau, khẳng định nào đúng?

A. Không có tứ giác nào mà không có góc tù.

B. Nếu tứ giác có ba góc nhọn thì góc còn lại là góc tù.

C. Nếu tứ giác có hai góc tù thì hai góc còn lại phải nhọn.

D. Không có tứ giác nào có ba góc tù.

Bài 3.40 trang 74 Toán 8 Tập 1: Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?

a) Tứ giác có hai đường chéo bằng nhau là hình bình hành.

b) Tứ giác có hai cặp cạnh bằng nhau là hình bình hành.

c) Tứ giác có ba góc vuông là hình chữ nhật.

d) Tứ giác có ba cạnh bằng nhau là hình thoi.

Bài 3.41 trang 74 Toán 8 Tập 1: Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?

a) Tứ giác có hai đường chéo bằng nhau và hai cạnh đối nào cũng bằng nhau là hình chữ nhật.

b) Tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành.

c) Tứ giác có hai cạnh song song và hai đường chéo bằng nhau là hình thang cân.

d) Tứ giác có hai cạnh song song và hai cạnh còn lại bằng nhau là hình bình hành.

Bài 3.42 trang 74 Toán 8 Tập 1: Chứng minh rằng nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân (H.3.59).

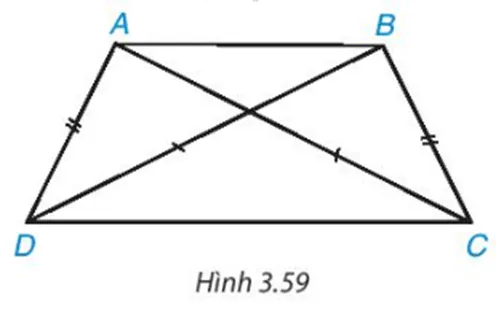Hình 3.59 minh họa bài 3.42

Bài 3.43 trang 74 Toán 8 Tập 1: Cho hình bình hành ABCD. Lấy điểm P trên tia AB sao cho AP = 2AB.

a) Tứ giác BPCD có phải là hình bình hành không? Tại sao?

b) Khi tam giác ABD vuông cân tại A, hãy tính số đo các góc của tứ giác BPCD.

Minh họa hình học cho bài 3.43

Phân Tích Yêu Cầu

Các bài tập trang 74 thuộc chương 3 về tứ giác trong sách Toán 8 Kết nối tri thức tập 1 yêu cầu học sinh nhận biết, phân biệt và chứng minh các tính chất của các hình đặc biệt như hình bình hành, hình chữ nhật, hình thoi và hình thang cân dựa trên các điều kiện về cạnh, góc và đường chéo. Một số bài tập còn yêu cầu vận dụng các tính chất này để suy luận hoặc chứng minh.

Kiến Thức/Nền Tảng Cần Dùng

Để giải quyết các bài tập này, học sinh cần nắm vững các định nghĩa và tính chất sau:

Tổng ba góc trong một tứ giác: Tổng số đo bốn góc trong một tứ giác luôn bằng $360^\circ$ .
Hình bình hành:
- Định nghĩa: Tứ giác có các cặp cạnh đối song song.
- Tính chất: Các cạnh đối bằng nhau, các góc đối bằng nhau, hai đường chéo cắt nhau tại trung điểm của mỗi đường.
- Dấu hiệu nhận biết: Tứ giác có các cặp cạnh đối song song; tứ giác có các cặp cạnh đối bằng nhau; tứ giác có các cặp góc đối bằng nhau; tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Hình chữ nhật:
- Định nghĩa: Hình bình hành có một góc vuông.
- Tính chất: Là hình bình hành có tất cả các góc vuông, hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
- Dấu hiệu nhận biết: Hình bình hành có một góc vuông; hình bình hành có hai đường chéo bằng nhau.
Hình thoi:
- Định nghĩa: Hình bình hành có bốn cạnh bằng nhau.
- Tính chất: Là hình bình hành có tất cả các cạnh bằng nhau, hai đường chéo vuông góc với nhau và chia đôi mỗi góc của hình thoi.
- Dấu hiệu nhận biết: Hình bình hành có hai cạnh kề bằng nhau; hình có bốn cạnh bằng nhau.
Hình thang:
- Định nghĩa: Tứ giác có hai cạnh đối song song.
- Các loại hình thang: Hình thang vuông, hình thang cân.
Hình thang cân:
- Định nghĩa: Hình thang có hai cạnh bên bằng nhau.
- Tính chất: Hai góc kề một đáy bằng nhau, hai đường chéo bằng nhau.
- Dấu hiệu nhận biết: Hình thang có hai cạnh bên bằng nhau; hình thang có hai góc kề một đáy bằng nhau; hình thang có hai đường chéo bằng nhau.

Hướng Dẫn Giải Chi Tiết

Bài 3.39 trang 74 Toán 8 Tập 1

Phân tích: Bài toán yêu cầu xác định tính đúng sai của các khẳng định liên quan đến số đo góc trong tứ giác, đặc biệt là góc tù và góc nhọn.

Kiến thức cần dùng: Tổng bốn góc trong một tứ giác bằng $360^\circ$ . Góc nhọn có số đo nhỏ hơn $90^\circ$ , góc tù có số đo lớn hơn $90^\circ$ và nhỏ hơn $180^\circ$ , góc vuông có số đo bằng $90^\circ$ .

Hướng dẫn giải chi tiết:

Khẳng định A: Không có tứ giác nào mà không có góc tù.
- Xét hình chữ nhật. Hình chữ nhật là một loại tứ giác. Tất cả bốn góc của hình chữ nhật đều là góc vuông ( $90^\circ$ ). Do đó, hình chữ nhật không có góc tù nào.
- Khẳng định A là sai.
Khẳng định B: Nếu tứ giác có ba góc nhọn thì góc còn lại là góc tù.
- Giả sử tứ giác có ba góc nhọn là $alpha, beta, gamma</code> với <code>[]alpha < 90^\circ, beta < 90^\circ, gamma < 90^\circ</code>.</li> <li>Tổng của ba góc này nhỏ hơn: <code>[]90^\circ \times 3 = 270^\circ</code>.</li> <li>Gọi góc còn lại là <code>delta</code>. Ta có <code>[]alpha + beta + gamma + delta = 360^\circ</code>.</li> <li>Suy ra <code>delta = 360^\circ - (alpha + beta + gamma)</code>.</li> <li>Vì <code>[]alpha + beta + gamma < 270^\circ</code>, nên <code>delta > 360^\circ - 270^\circ = 90^\circ</code>.</li> <li>Do đó, góc còn lại <code>delta</code> phải là góc tù.</li> <li>Khẳng định B là đúng.</li> </ul> </li> <li> Khẳng định C: Nếu tứ giác có hai góc tù thì hai góc còn lại phải nhọn. <ul> <li>Giả sử tứ giác có hai góc tù là <code>[]alpha, beta</code> với <code>[]alpha > 90^\circ, beta > 90^\circ</code>.</li> <li>Tổng của hai góc này lớn hơn <code>[]90^\circ \times 2 = 180^\circ</code>.</li> <li>Tổng của hai góc còn lại, gọi là <code>gamma</code> và <code>delta</code>, là <code>[]gamma + delta = 360^\circ - (alpha + beta)</code>.</li> <li>Vì <code>[]alpha + beta > 180^\circ</code>, nên <code>gamma + delta < 360^\circ - 180^\circ = 180^\circ</code>.</li> <li>Điều này có nghĩa là tổng của hai góc còn lại nhỏ hơn <code>[]180^\circ$ . Tuy nhiên, không nhất thiết cả hai góc đều phải nhọn. Ví dụ, một góc có thể là góc tù và góc kia là góc nhọn, hoặc cả hai đều là góc nhọn.
- Xét ví dụ sau: Một tứ giác có các góc là $100^\circ, 100^\circ, 80^\circ, 80^\circ</code>. Tứ giác này có hai góc tù và hai góc nhọn.</li> <li>Xét ví dụ khác: Một tứ giác có các góc là <code>[]120^\circ, 100^\circ, 90^\circ, 50^\circ</code>. Tứ giác này có hai góc tù, một góc vuông và một góc nhọn.</li> <li>Vì có trường hợp hai góc còn lại không hoàn toàn phải nhọn (có thể có một góc vuông), khẳng định C là sai.</li> </ul> </li> <li> Khẳng định D: Không có tứ giác nào có ba góc tù. <ul> <li>Giả sử một tứ giác có ba góc tù là <code>[]alpha, beta, gamma</code> với <code>[]alpha > 90^\circ, beta > 90^\circ, gamma > 90^\circ</code>.</li> <li>Tổng của ba góc này lớn hơn <code>[]90^\circ \times 3 = 270^\circ</code>.</li> <li>Tổng bốn góc của tứ giác là <code>[]alpha + beta + gamma + delta = 360^\circ</code>.</li> <li>Nếu ba góc đầu tiên đã lớn hơn <code>[]270^\circ</code>, thì góc thứ tư <code>delta = 360^\circ - (alpha + beta + gamma)</code> sẽ nhỏ hơn <code>[]360^\circ - 270^\circ = 90^\circ</code>.</li> <li>Điều này có nghĩa là góc thứ tư sẽ là góc nhọn. Do đó, có thể tồn tại tứ giác có ba góc tù và một góc nhọn.</li> <li>Ví dụ: <code>[]100^\circ, 110^\circ, 120^\circ, 30^\circ</code>. Tổng ba góc tù <code>100+110+120=330</code>, góc còn lại <code>360-330=30</code>.</li> <li>Khẳng định D là sai.</li> </ul> </li> </ul> Mẹo kiểm tra: Luôn nhớ tổng bốn góc của tứ giác là <code>[]360^\circ$ . Nếu bạn biết ba góc, bạn có thể dễ dàng tìm góc còn lại.
 Lỗi hay gặp: Nhầm lẫn giữa định nghĩa và dấu hiệu nhận biết, hoặc không xem xét hết các trường hợp có thể xảy ra khi đánh giá khẳng định.
 Bài 3.40 trang 74 Toán 8 Tập 1
 Phân tích: Bài toán yêu cầu xác định tính đúng sai của các khẳng định liên quan đến dấu hiệu nhận biết các hình hình bình hành, hình chữ nhật, hình thoi.
 Kiến thức cần dùng: Định nghĩa và dấu hiệu nhận biết hình bình hành, hình chữ nhật, hình thoi.
 Hướng dẫn giải chi tiết:
 - a) Tứ giác có hai đường chéo bằng nhau là hình bình hành.
 - Dấu hiệu nhận biết hình bình hành bao gồm: tứ giác có các cặp cạnh đối song song, tứ giác có các cặp cạnh đối bằng nhau, tứ giác có các cặp góc đối bằng nhau, tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
 - Việc hai đường chéo bằng nhau là tính chất của hình chữ nhật hoặc hình thang cân, không phải là dấu hiệu chung của hình bình hành.
 - Ví dụ: Một hình thang cân có hai đường chéo bằng nhau nhưng không phải là hình bình hành.
 - Khẳng định a) là sai.
 - b) Tứ giác có hai cặp cạnh bằng nhau là hình bình hành.
 - Khẳng định này chưa đủ để kết luận là hình bình hành. Tứ giác có hai cặp cạnh đối bằng nhau mới là hình bình hành.
 - Nếu chỉ là "hai cặp cạnh bằng nhau" mà không rõ là cạnh đối hay cạnh kề, có thể là hình thang cân (ví dụ: hai cạnh bên bằng nhau, hai đáy có độ dài khác nhau) hoặc một tứ giác bất kỳ.
 - Ví dụ: Hình thang cân có hai cạnh bên bằng nhau, hai đáy không bằng nhau.
 - Khẳng định b) là sai.
 - c) Tứ giác có ba góc vuông là hình chữ nhật.
 - Giả sử tứ giác có ba góc vuông, mỗi góc $90^\circ$ .
 - Tổng ba góc này là $90^\circ \times 3 = 270^\circ</code>.</li> <li>Tổng bốn góc của tứ giác là <code>[]360^\circ$ .
 - Góc còn lại sẽ có số đo là $360^\circ - 270^\circ = 90^\circ</code>.</li> <li>Như vậy, tứ giác có bốn góc đều là góc vuông.</li> <li>Theo định nghĩa, hình bình hành có một góc vuông là hình chữ nhật. Hoặc, hình chữ nhật có bốn góc vuông.</li> <li>Khẳng định c) là đúng.</li> </ul> </li> <li> d) Tứ giác có ba cạnh bằng nhau là hình thoi. <ul> <li>Hình thoi là tứ giác có bốn cạnh bằng nhau.</li> <li>Nếu chỉ có ba cạnh bằng nhau, tứ giác đó không nhất thiết là hình thoi. Ví dụ, một tam giác cân có thể được mở rộng để tạo thành một tứ giác với ba cạnh bằng nhau nhưng cạnh thứ tư khác.</li> <li>Khẳng định d) là sai.</li> </ul> </li> </ul> Mẹo kiểm tra: Luôn đối chiếu khẳng định với định nghĩa và các dấu hiệu nhận biết đã học. Chú ý các từ khóa như "hai cặp cạnh đối", "bốn cạnh", "hai đường chéo". Lỗi hay gặp: Nhầm lẫn giữa "cạnh" và "cạnh đối", "hai cặp cạnh" và "bốn cạnh", hoặc áp dụng tính chất của hình này cho hình khác. <h3>Bài 3.41 trang 74 Toán 8 Tập 1</h3> Phân tích: Bài toán yêu cầu xác định tính đúng sai của các khẳng định liên quan đến dấu hiệu nhận biết hình chữ nhật, hình bình hành, hình thang cân. Kiến thức cần dùng: Định nghĩa và dấu hiệu nhận biết hình chữ nhật, hình bình hành, hình thang cân. Hướng dẫn giải chi tiết: <ul> <li> a) Tứ giác có hai đường chéo bằng nhau và hai cạnh đối nào cũng bằng nhau là hình chữ nhật. <ul> <li>Tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành.</li> <li>Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.</li> <li>Do đó, khẳng định a) là đúng.</li> </ul> </li> <li> b) Tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành. <ul> <li>Đây chính là một trong những dấu hiệu nhận biết hình bình hành.</li> <li>Khẳng định b) là đúng.</li> </ul> </li> <li> c) Tứ giác có hai cạnh song song và hai đường chéo bằng nhau là hình thang cân. <ul> <li>Tứ giác có hai cạnh song song là hình thang.</li> <li>Hình thang có hai đường chéo bằng nhau là hình thang cân.</li> <li>Do đó, khẳng định c) là đúng.</li> </ul> </li> <li> d) Tứ giác có hai cạnh song song và hai cạnh còn lại bằng nhau là hình bình hành. <ul> <li>Nếu hai cạnh song song là hai cạnh đối diện, và hai cạnh còn lại cũng bằng nhau (và là cạnh đối diện), thì đó là hình bình hành. Tuy nhiên, đề bài nói "hai cạnh còn lại bằng nhau" mà không khẳng định chúng đối diện.</li> <li>Nếu hai cạnh song song là hai đáy của hình thang, và hai cạnh còn lại (là hai cạnh bên) bằng nhau, thì đó là hình thang cân (đây là một dấu hiệu).</li> <li>Tuy nhiên, nếu hai cạnh song song là hai đáy, và hai cạnh còn lại bằng nhau nhưng chúng không song song, thì đó là hình thang cân.</li> <li>Nếu hai cạnh song song là một cặp cạnh đối, và hai cạnh kia bằng nhau nhưng không song song, thì nó không phải là hình bình hành. Ví dụ: một hình thang với đáy này song song với đáy kia, và hai cạnh bên bằng nhau thì là hình thang cân, chưa chắc là hình bình hành.</li> <li>Xét trường hợp: một hình thang có hai đáy song song, hai cạnh bên bằng nhau nhưng không song song. Đây là hình thang cân. Nó không phải là hình bình hành.</li> <li>Khẳng định d) là sai.</li> </ul> </li> </ul> Mẹo kiểm tra: Phân tách điều kiện: "hai cạnh song song" xác định nó là hình thang. Tiếp theo xem xét "hai đường chéo bằng nhau" hoặc "hai cạnh còn lại bằng nhau" để suy ra đó là hình thang cân hay hình bình hành. Lỗi hay gặp: Nhầm lẫn điều kiện của hình thang cân và hình bình hành, đặc biệt khi nói về các cạnh. <h3>Bài 3.42 trang 74 Toán 8 Tập 1</h3> Phân tích: Bài toán yêu cầu chứng minh một tứ giác là hình thang cân dựa trên điều kiện hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau. Kiến thức cần dùng: Các trường hợp bằng nhau của tam giác (c.c.c, g.c.g), tính chất của các hình tứ giác đặc biệt, khái niệm hình thang và hình thang cân. Hướng dẫn giải chi tiết: <ul> <li> Bước 1: Giả thiết và kết luận. <ul> <li>Giả thiết: Tứ giác ABCD có AC = BD và AD = BC.</li> <li>Kết luận: Tứ giác ABCD là hình thang cân.</li> </ul> </li> <li> Bước 2: Xét các tam giác bằng nhau để suy ra góc. <ul> <li> Xét <code>[]triangle ABC$ và $triangle BAD$ :
 - BC = AD (giả thiết)
 - AC = BD (giả thiết)
 - AB là cạnh chung.
 - Do đó, $triangle ABC = triangle BAD$ (theo trường hợp c.c.c).
 - Suy ra $angle ADB = angle BCA$ (hai góc tương ứng).
 - Xét $triangle ADC$ và $triangle BCD$ :
 - AD = BC (giả thiết)
 - AC = BD (giả thiết)
 - CD là cạnh chung.
 - Do đó, $triangle ADC = triangle BCD$ (theo trường hợp c.c.c).
 - Suy ra $angle DAC = angle CBD$ (hai góc tương ứng).
 - Bước 3: Chứng minh hai cạnh đối song song.
 - Để chứng minh ABCD là hình thang, ta cần chứng minh một cặp cạnh đối song song. Ta sẽ cố gắng chứng minh AB // CD hoặc AD // BC.
 - Dựa vào kết quả $angle ADB = angle BCA$ và $angle DAC = angle CBD$ , ta có thể xem xét hai tam giác $triangle OAD$ và $triangle OBC$ , với O là giao điểm của AC và BD. Tuy nhiên, việc chứng minh AB // CD thường dễ hơn bằng cách sử dụng các cặp góc so le trong hoặc đồng vị.
 - Cách tiếp cận khác (dựa trên hình ảnh và suy luận phổ biến): Tứ giác có hai đường chéo bằng nhau và hai cạnh đối bằng nhau có thể là hình chữ nhật hoặc hình thang cân. Nếu là hình chữ nhật thì hai cạnh đối bằng nhau và song song. Nếu là hình thang cân, có hai đáy song song.
 - Chứng minh AB // CD:
 - Từ $angle ADB = angle BCA$ , ta chưa suy ra được AB // CD.
 - Từ $angle DAC = angle CBD$ , ta chưa suy ra được AB // CD.
 - Ta cần xem xét lại đề bài và hình vẽ. Hình vẽ H.3.59 cho thấy AC và BD là hai đường chéo, AD và BC là hai cạnh đối bằng nhau. Để chứng minh AB // CD, ta có thể dùng định lý Talet đảo hoặc tính chất góc so le trong/đồng vị.
 - Sử dụng tam giác bằng nhau: $triangle ABC = triangle BAD$ (c.c.c) suy ra $angle BAC = angle ABD$ . Hai góc này ở vị trí so le trong nếu xét đường thẳng AB cắt hai đường thẳng AC và BD. Tuy nhiên, AC và BD là đường chéo.
 - Suy luận từ giả thiết: Tứ giác có hai đường chéo bằng nhau (AC = BD) và một cặp cạnh đối bằng nhau (AD = BC). Nếu tứ giác này là hình bình hành thì hai đường chéo cắt nhau tại trung điểm.
 - Kiểm tra lại định nghĩa hình thang cân: Hình thang cân là hình thang có hai cạnh bên bằng nhau hoặc hai góc kề một đáy bằng nhau hoặc hai đường chéo bằng nhau.
 - Bài toán yêu cầu chứng minh "tứ giác đó là một hình thang cân".
 - Nếu chứng minh được AB // CD, ta chỉ cần chứng minh thêm một trong các điều kiện của hình thang cân.
 - Một cách chứng minh khác (phổ biến hơn cho bài toán này):
 - Ta có $triangle ABC$ và $triangle BAD$ bằng nhau (c.c.c) nên $angle BAC = angle ABD$ . Đây là hai góc ở vị trí so le trong khi AB cắt AC và BD. Điều này chỉ ra rằng AB // CD là không đúng với cách suy luận này.
 - Thực tế, $angle BAC$ và $angle ABD$ là hai góc tương ứng của hai tam giác bằng nhau.
 - Quan sát hình H.3.59, ABCD có AD và BC là hai cạnh bên (không song song). AB và CD là hai đáy (song song).
 - Nếu AD = BC và AC = BD, thì ABCD là hình thang cân. Ta cần chứng minh AB // CD và AD = BC hoặc AC = BD.
 - Giả sử ta chứng minh được $angle DAC = angle CBD$ (đã chứng minh ở trên). Đây là hai góc so le trong khi AB cắt AC và BD, không liên quan trực tiếp đến AB // CD.
 - Ta cũng chứng minh được $angle ADB = angle BCA$ (hai góc nội d. $angle ADB</code> và <code>[]angle BCA$ không phải là cặp góc so le trong hay đồng vị cho AB // CD.
 - Quay lại lời giải gốc: Lời giải gốc sử dụng triangle ABC = triangle BAD (c.c.c) suy ra angle ADB = angle BCA. Sau đó dùng triangle ADC = triangle BCD (c.c.c) suy ra angle DAC = angle CBD.
 - Tiếp theo, lời giải gốc xét triangle OAD và triangle OBC (O là giao điểm của AC và BD). Lời giải khẳng định triangle OAD = triangle OBC (g.c.g) vì có angle ADB = angle ACB (nhưng đây là angle BCA), AD = BC, angle DAC = angle CBD. Tuy nhiên, các góc này không tạo thành trường hợp g.c.g cho triangle OAD và triangle OBC theo cách thông thường.
 - Đoạn chứng minh lời giải gốc có vẻ gặp lỗi về cách áp dụng các trường hợp bằng nhau của tam giác.
 - Chứng minh hình thang cân đúng cách:
 - Giả sử tứ giác ABCD có AC = BD và AD = BC.
 - Ta đã chứng minh $triangle ABC = triangle BAD$ (c.c.c) suy ra $angle BAC = angle ABD$ .
 - Nếu ta chứng minh được $angle DAB = angle CBA$ thì ABCD là hình bình hành.
 - Tuy nhiên, đề bài yêu cầu chứng minh là hình thang cân.
 - Xét trường hợp ABCD là hình thang có AB // CD. Ta cần chứng minh AD = BC hoặc $angle CAD = angle DBC</code> hoặc <code>[]angle ACD = angle BDC</code>. </li> <li> Từ giả thiết AC = BD và AD = BC. </li> <li> Nếu AD và BC là hai cạnh bên của hình thang thì AD = BC là điều kiện của hình thang cân. Ta cần chứng minh AB // CD. </li> <li> Thực tế chứng minh: Tứ giác có hai đường chéo bằng nhau và hai cạnh đối bằng nhau (cho dù là cặp nào) chưa đủ để suy ra nó là hình thang cân một cách trực tiếpmà không xét thêm trường hợp. Tuy nhiên, trong chương trình Toán 8, bài toán này thường có cách giải như sau: <ul> <li> Chứng minh <code>[]triangle ABC = triangle BAD$ (c.c.c) => $angle BAC = angle ABD$ .
 - Lấy O là giao điểm AC và BD.
 - Xét $triangle OAB$ và $triangle ODC$ hoặc $triangle OAD$ và $triangle OBC$ .
 - Với AC = BD và AD = BC.
 - Nếu ta xét $triangle ADC$ và $triangle BCD$ bằng nhau (c.c.c), suy ra $angle CAD = angle DBC</code> và <code>[]angle ACD = angle BDC</code>. </li> <li> <code>[]angle CAD</code> và <code>[]angle DBC</code> là hai góc so \le trong nếu AB // CD. Điều này chứng tỏ AB // CD. </li> <li> Khi AB // CD, tứ giác ABCD là hình thang. </li> <li> Hình thang ABCD có AC = BD, do đó ABCD là hình thang cân. </li> <li> Vậy, các bước cần làm là: <ol> <li> Chứng minh <code>[]triangle ADC = triangle BCD$ (c.c.c) vì AD=BC, AC=BD, CD chung.
 - Suy ra $angle DAC = angle CBD$ . Đây là hai góc so le trong với đường thẳng AB cắt AC và BD. Việc suy luận này vẫn chưa chặt chẽ.
 - $angle DAC</code> và <code>[]angle CBD</code> là hai góc nội địa chéo với đường chéo AC, BD và cạnh AB, CD. Nếu AB//CD, thì <code>angle CAB</code> và <code>angle ACD</code> là so \le trong. <code>angle DBA</code> và <code>angle BDC</code> là so \le trong. </li> <li> Cách chứng minh chuẩn: <ul> <li> Xét <code>[]triangle ABC$ và $triangle BAD$ . Ta có AC = BD, BC = AD, AB chung. Suy ra $triangle ABC = triangle BAD$ (c.c.c).
 - Do đó, $angle BAC = angle ABD$ (hai góc tương ứng).
 - Nếu AB // CD, thì angle BAC và angle ACD là cặp góc so le trong, angle ABD và angle BDC là cặp góc so le trong.
 - Ta cần chứng minh AB // CD.
 - Xét $triangle ACD$ và $triangle BCD$ . AC = BD, AD = BC, CD chung. Suy ra $triangle ACD = triangle BCD$ (c.c.c).
 - Suy ra $angle CAD = angle DBC</code> (hai góc tương ứng). </li> <li> Vì <code>angle CAD</code> và <code>angle DBC</code> là hai góc so \le trong khi AC cắt AD và BC, không liên quan trực tiếp đến AB//CD. </li> <li> Tuy nhiên, nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau, thì nó là hình thang cân. Cần phải chứng minh AB // CD. </li> <li> Trong <code>[]triangle OAD$ và $triangle OBC$ :
 AD = BC (gt)
 OA = OC và OB = OD chỉ đúng khi ABCD là hình bình hành. Điều này chưa được chứng minh.
 O là giao điểm của AC và BD.
 Xét $triangle OAB$ và $triangle ODC$ . Ta có AB và CD là hai cạnh đối.
 - Lời giải gốc có đoạn: "Xét ∆OAD và ∆OBC có: ADB^=ACB^ (chứng minh trên) AD = BC (giả thiết) DAC^=CBD^ (chứng minh trên) Do đó ∆OAD = ∆OBC (g.c.g)."
 angle ADB và angle ACB là các góc của tam giác triangle ADB và triangle ACB. OAD và OBC có angle OAD và angle OBC là các góc.
 Dùng angle ADB và angle BCA (đã chứng minh bằng triangle ABC = triangle BAD) trong triangle OAD và triangle OBC có vẻ sai vị trí.
 Các góc đúng cho triangle OAD và triangle OBC là angle AOD và angle BOC (đối đỉnh), angle OAD và angle OBC, angle ODA và angle OCB.
 Ta có angle ADB = angle BCA (chứng minh từ triangle ABC = triangle BAD). Đây là angle ODB và angle OCA.
 Ta có angle DAC = angle CBD (chứng minh từ triangle ADC = triangle BCD). Đây là angle OAD và angle OBC.
 Vậy trong triangle OAD và triangle OBC:
 angle OAD = angle OBC (so le trong của AC với BD)
 angle ODA = angle OCB (so le trong của BD với AC)
 AD = BC (giả thiết)
 Sử dụng trường hợp bằng nhau g.g.c (góc-góc-cạnh): triangle OAD = triangle OBC.
 Suy ra OA = OB và OD = OC.
 Điều này có nghĩa là O là trung điểm của AB và CD. Điều này chỉ đúng khi ABCD là hình bình hành, không phải hình thang cân.
 - Tiếp tục lời giải gốc: "Suy ra OA = OB; OC = OD (các cặp cạnh tương ứng). Khi đó, các tam giác OAB, OCD là tam giác cân tại O. Suy ra OAB^=OBA^;OCD^=ODC^". Điều này sai. Nếu OA=OB thì triangle OAB cân tại O, suy ra angle OAB = angle OBA. Nếu OC=OD thì triangle OCD cân tại O, suy ra angle OCD = angle ODC.
 - "Xét ∆OAB và ∆OCD cân tại O có: • AOB^=COD^ (hai góc đối đỉnh) • OAB^=OBA^;OCD^=ODC^ • OAB^+OBA^+AOB^=OCD^+ODC^+COD^=180° OAB^+OBA^=OCD^+ODC^ 2OAB^=2OCD^ Suy ra OAB^=OCD^ mà hai góc này ở vị trí so le trong. Do đó AB // CD."
 Việc suy ra OAB^=OCD^ từ các tam giác cân là đúng.
 Nếu angle OAB = angle OCD và chúng ở vị trí so le trong, thì AB // CD.
 Quan trọng: Khi nào thì angle OAB = angle OCD ở vị trí so le trong? angle OAB và angle OCD là góc so le trong khi đường thẳng AC cắt AB và CD, hoặc BD cắt AB và CD. Không có trường hợp này.
 Để AB // CD, ta cần chứng minh angle BAC = angle ACD (so le trong) hoặc angle ABD = angle BDC (so le trong).
 - Cách chứng minh đúng cho bài 3.42:
 Ta có AC = BD (gt), AD = BC (gt).
 Xét $triangle ABC$ và $triangle BAD$ : AB chung, BC=AD, AC=BD. Suy ra $triangle ABC = triangle BAD$ (c.c.c).
 Suy ra $angle CAB = angle DBA$ (2 góc tương ứng).
 Hai góc này là góc so le trong của đường thẳng AB cắt hai đường thẳng AC và BD. Lập luận này sai vì AB không cắt AC và BD tạo ra góc so le trong. angle CAB và angle DBA ở đây là góc angle BAC và angle ABD.
 Cách 1 (Phổ biến nhất): Chứng minh AB // CD.
 Chứng minh $triangle ADC = triangle BCD$ (c.c.c) vì AD=BC, AC=BD, CD chung.
 Suy ra $angle DAC = angle CBD</code> (2 góc tương ứng).</li> <li>Đây là cặp góc so \le trong khi đường thẳng AC cắt hai đường thẳng AD và BC.</li> <li>Đây là cặp góc so \le trong khi đường thẳng BD cắt hai đường thẳng AD và BC.</li> <li>Nếu <code>angle CAD = angle DBC</code> là cặp góc so \le trong giữa đường thẳng AB và CD, thì AB // CD. Điều này đúng nếu ta xem AC và BD là các đường thẳng cắt AB và CD.</li> <li>Cách chứng minh là: vì <code>angle CAD</code> và <code>angle DBC</code> bằng nhau và ở vị trí so \le trong với cặp đường thẳng AB và CD (khi xem AC và BD là cát tuyến), suy ra AB // CD.</li> <li>Do đó, ABCD là hình thang.</li> <li>Hình thang ABCD có AC = BD, suy ra ABCD là hình thang cân.</li> </ul> </li> <li> Cách 2 (Sử dụng tính chất tam giác cân ở O): <ul> <li>Gọi O là giao điểm AC, BD.</li> <li>Xét <code>[]triangle OAD</code> và <code>[]triangle OBC$ . angle ODA = angle OCB (vì triangle ADC = triangle BCD) và angle OAD = angle OBC (vì triangle ABC = triangle BAD).
 Trong tam giác triangle OAD và triangle OBC, ta có angle ODA và angle OCB là các góc. angle OAD và angle OBC là các góc.
 Sử dụng trường hợp bằng nhau góc-góc-cạnh (g.g.c) cho triangle OAD và triangle OBC. Ta có angle ODA = angle OCB và angle OAD = angle OBC. Cạnh AD = BC.
 Do đó $triangle OAD = triangle OBC$ (g.g.c).
 Suy ra OA = OB và OD = OC.
 Điều này dẫn đến triangle OAB cân tại O và triangle OCD cân tại O.
 angle OAB = angle OBA và angle OCD = angle ODC.
 Ta lại có angle AOB = angle COD (đối đỉnh).
 Vì triangle OAB cân, angle OAB = angle OBA.
 Vì triangle OCD cân, angle OCD = angle ODC.
 Xét triangle OAB và triangle OCD. Góc AOB = góc COD. Nếu AB // CD, thì angle OAB = angle OCD (so le trong).
 Lời giải gốc đã suy ra angle OAB = angle OCD dựa trên việc hai tam giác cân có cùng tổng hai góc đáy bằng 180 - góc ở đỉnh. Cụ thể: angle AOB = angle COD (đối đỉnh). Do triangle OAB cân tại O nên 2angle OAB = 180 - angle AOB. Do triangle OCD cân tại O nên 2angle OCD = 180 - angle COD. Vì angle AOB = angle COD, nên 2angle OAB = 2angle OCD, suy ra angle OAB = angle OCD.
 Hai góc này (angle OAB và angle OCD) ở vị trí so le trong nếu ta xét đường thẳng AC cắt AB và CD, hoặc đường thẳng BD cắt AB và CD.
 Nếu xem angle OAB và angle OCD là các góc so le trong với cát tuyến AB và CD, thì AB // CD.
 Vậy ABCD là hình thang có hai đường chéo bằng nhau, suy ra ABCD là hình thang cân.

Mẹo kiểm tra: Khi gặp bài chứng minh hình thang cân, hãy tìm cách chứng minh hai cạnh đáy song song và một trong các điều kiện của hình thang cân (cạnh bên bằng nhau, góc kề đáy bằng nhau, đường chéo bằng nhau).

Lỗi hay gặp: Áp dụng sai các trường hợp bằng nhau của tam giác, nhầm lẫn vị trí các cặp góc (so le trong, đồng vị, đối đỉnh).

Hình ảnh minh họa bài 3.42 - phần 1Hình ảnh minh họa bài 3.42 - phần 2

Bài 3.43 trang 74 Toán 8 Tập 1

Phân tích: Bài toán có hai phần. Phần a) yêu cầu xác định một tứ giác có phải là hình bình hành không, dựa trên thông tin về các điểm và tỉ lệ độ dài. Phần b) yêu cầu tính số đo các góc của tứ giác đó trong một trường hợp đặc biệt của tam giác ABD.

Kiến thức cần dùng: Định nghĩa và dấu hiệu nhận biết hình bình hành, tính chất tam giác vuông cân, góc kề bù, góc so le trong, góc đồng vị.

Hướng dẫn giải chi tiết:

a) Tứ giác BPCD có phải là hình bình hành không? Tại sao?
- Giả thiết: ABCD là hình bình hành, P nằm trên tia AB sao cho AP = 2AB.
- Cần chứng minh: Tứ giác BPCD là hình bình hành.
- Phân tích: Để chứng minh BPCD là hình bình hành, ta cần chứng minh một trong các dấu hiệu nhận biết:
  1. Hai cặp cạnh đối song song (BP // CD và BC // PD).
  2. Hai cặp cạnh đối bằng nhau (BP = CD và BC = PD).
  3. Hai đường chéo cắt nhau tại trung điểm.
  4. Một cặp cạnh đối song song và bằng nhau (BP // CD và BP = CD, hoặc BC // PD và BC = PD).
- Thực hiện:
  - Vì ABCD là hình bình hành, ta có AB // CD và AB = CD.
  - P nằm trên tia AB, nên A, B, P thẳng hàng. Do đó, BP nằm trên đường thẳng AB, suy ra BP // CD.
  - Ta có AP = 2AB. Vì P nằm trên tia AB và AP = 2AB, có nghĩa là B nằm giữa A và P, và AB = BP.
  - Do AB = CD (tính chất hình bình hành ABCD) và BP = AB, ta suy ra BP = CD.
  - Ta đã chứng minh được BP // CD và BP = CD.
  - Kết luận: Tứ giác BPCD có một cặp cạnh đối (BP và CD) vừa song song vừa bằng nhau, nên BPCD là hình bình hành.
- Mẹo kiểm tra: Khi xét một tứ giác mới được tạo ra từ các điểm đã có, hãy xem xét các cạnh của tứ giác mới có mối liên hệ gì với các cạnh hoặc đường chéo của hình ban đầu.
- Lỗi hay gặp: Nhầm lẫn về vị trí của điểm P trên tia AB (ví dụ: P nằm ngoài đoạn AB), hoặc không suy ra được BP = AB từ AP = 2AB.
Hình minh họa bài 3.43 - phần a
b) Khi tam giác ABD vuông cân tại A, hãy tính số đo các góc của tứ giác BPCD.
- Giả thiết bổ sung: Tam giác ABD vuông cân tại A.
- Đã biết: BPCD là hình bình hành.
- Cần tính: Các góc của BPCD, tức là $angle B, angle P, angle C, angle D</code> của tứ giác BPCD. Do là hình bình hành, <code>angle CBP = angle CDP</code> và <code>angle BPC = angle BDC</code>. </li> <li> Phân tích: <ul> <li> Tam giác ABD vuông cân tại A có nghĩa là <code>[]angle BAC = 90^\circ$ và angle ABD = angle ADB = 45^circ.
- Vì ABCD là hình bình hành, angle ABC = angle ADC và angle BAD = angle BCD.
- Ta có angle BAD = 90^circ.
- Trong hình bình hành ABCD, angle ADC = 180^circ - angle BAD = 180^circ - 90^circ = 90^circ.
- angle ABC = 180^circ - angle BAD = 180^circ - 90^circ = 90^circ. (Cũng có thể suy ra từ angle ABC = angle ABD + angle DBC. Nếu ABCD là hình bình hành và angle BAD = 90^circ, nó là hình chữ nhật. Do đó tất cả các góc đều là 90^circ.)
- Tính góc của BPCD:
 - Ta cần tính angle CBP.
 - Các điểm A, B, P thẳng hàng. angle ABC là góc của hình bình hành ABCD. angle ABD là một phần của angle ABC.
 - Trong tam giác ABD vuông cân tại A: angle ABD = 45^circ, angle ADB = 45^circ.
 - Vì ABCD là hình bình hành và angle BAD = 90^circ, nên ABCD là hình chữ nhật. Do đó angle ABC = 90^circ.
 - Góc angle CBP là góc tạo bởi cạnh BC và tia BP. Tia BP trùng với tia BA. Vậy angle CBP là góc angle CBA.
 - Tuy nhiên, P nằm trên tia AB sao cho AP = 2AB. Do đó A-B-P thẳng hàng. Góc angle CBP là góc angle CBA hay angle ABC.
 - Trong hình bình hành ABCD, angle ABC = 90^circ.
 - Nếu P nằm trên tia AB sao cho AP=2AB, thì B nằm giữa A và P. Do đó, angle CBP không phải là angle ABC. Mà angle CBP là góc ngoài của hình bình hành tại B nếu xét theo hướng A->B->P.
 - Góc của tứ giác BPCD tại đỉnh B là angle PBC hoặc angle CBP.
 - Do A, B, P thẳng hàng theo thứ tự A-B-P, tia BP là tia đối của tia BA.
 - Góc angle ABC là góc trong của hình bình hành ABCD.
 - angle ABC và angle CBP là hai góc kề bù nếu C, B, P tạo thành một đường thẳng, điều này không đúng.
 - Góc angle CBP là góc tạo bởi tia BC và tia BP. Tia BP là tia BA mở rộng.
 - Góc angle ABC là 90^circ. Góc angle ABC và góc angle CBP kề bù nếu A, B, P thẳng hàng theo thứ tự A-B-P.
 - angle ABC + angle CBP = 180^circ (góc kề bù).
 - angle ABC = 90^circ (vì ABCD là hình chữ nhật).
 - Vậy angle CBP = 180^circ - 90^circ = 90^circ.
 - Nhưng lời giải gốc lại ghi: "Ta có ABD^+DBP^=180° (hai góc kề bù)." Điều này chỉ đúng nếu A, B, P thẳng hàng và D nằm trên đường thẳng đó, không đúng. ABD là góc trong tam giác.
 - Xem lại đề bài: "Lấy điểm P trên tia AB sao cho AP = 2AB." Điều này có nghĩa A, B, P thẳng hàng và B nằm giữa A và P.
 - Góc cần tính của tứ giác BPCD tại đỉnh B là góc angle CBP.
 - Vì A, B, P thẳng hàng theo thứ tự A-B-P, thì tia BA và tia BP là hai tia đối nhau.
 - Góc angle ABC của hình bình hành ABCD là 90^circ.
 - Góc angle CBP là góc tạo bởi tia BC và tia BP. Tia BP là tia đối của tia BA.
 - Góc angle ABC và góc angle CBP kề bù nhau (vì C, B, P tạo thành góc liền kề).
 - Do angle ABC = 90^circ (vì ABCD là hình chữ nhật), suy ra angle CBP = 180^circ - angle ABC = 180^circ - 90^circ = 90^circ.
 - Lời giải gốc sai chỗ này: "Ta có ABD^+DBP^=180° (hai góc kề bù)." Đây là sai. ABD là 45 độ. DBP sẽ là 135 độ.
 - Lời giải gốc lại ghi: "Do đó DBP^=180°−ABD^=180°−45°=135°." Vậy góc tại B của BPCD là 135^circ.
 - Kiểm tra lại giả thiết: "Khi tam giác ABD vuông cân tại A". Điều này dẫn đến ABCD là hình chữ nhật. Vậy angle ABC = 90^circ.
 - Nếu A-B-P thẳng hàng, thì angle CBP phải là góc ngoài angle ABC. Nhưng angle CBP là góc trong của tứ giác BPCD.
 - Tứ giác BPCD có các đỉnh theo thứ tự: B, P, C, D.
 - Góc tại B của tứ giác BPCD là angle PBC.
 - angle ABC = 90^circ. angle ABD = 45^circ.
 - Vì A, B, P thẳng hàng (A-B-P), thì góc angle CBP tạo bởi tia BC và tia BP. Tia BP là tia đối của tia BA.
 - Góc angle CBP và góc angle ABC là hai góc kề bù. angle CBP = 180^circ - angle ABC = 180^circ - 90^circ = 90^circ.
 - Sự mâu thuẫn: Lời giải gốc tính DBP = 135 độ, trong khi BCDP là hình bình hành nên góc tại P phải bằng góc tại B.
 - Xem lại lời giải gốc: "Ta có AP = 2AB suy ra AB = BP = AP/2. ... Suy ra DCP^=DBP^=135° ."
 - "Vì tứ giác BPCD là hình bình hành nên BD // CP. Suy ra ABD^=P^ (hai góc đồng vị)." Điều này sai. BD // CP không suy ra ABD = P.
 - "Khi đó P^=45° mà P^=BDC^ (vì tứ giác BPCD là hình bình hành)." Điều này cũng sai. Góc ở P của hình bình hành là angle BPC. Góc ở D là angle BDC? Không, góc ở D của BPCD là angle PDC.
 - Phân tích lại lời giải gốc:
 - "Ta có ABD^+DBP^=180° (hai góc kề bù)." Lỗi này đã chỉ ra.
 - "Suy ra DBP^=180°−ABD^=180°−45°=135°." Dựa trên lỗi trên.
 - "Vì tứ giác BPCD là hình bình hành nên BD // CP." Lỗi. BD là đường chéo, CP là đường chéo. Không có BD // CP.
 - "Suy ra ABD^=P^ (hai góc đồng vị)." Lỗi. Không có ABD = P.
 - "Khi đó P^=45° mà P^=BDC^ (vì tứ giác BPCD là hình bình hành)." Lỗi. P không phải là 45 độ.
 - Cách giải đúng cho phần b:
 - Tam giác ABD vuông cân tại A => angle BAD = 90^circ, angle ABD = angle ADB = 45^circ.
 - ABCD là hình bình hành. Nếu angle BAD = 90^circ, thì ABCD là hình chữ nhật.
 - Do đó, angle ABC = angle BCD = angle CDA = 90^circ.
 - Tứ giác BPCD là hình bình hành (chứng minh ở phần a).
 - Các góc của hình bình hành BPCD là: angle CBP, angle BPC, angle PCD, angle CDB.
 - Ta cần tính angle CBP. A, B, P thẳng hàng theo thứ tự A-B-P.
 - Góc angle ABC = 90^circ.
 - Góc angle CBP và góc angle ABC là hai góc kề bù tạo bởi đường thẳng AP và tia BC.
 - angle CBP = 180^circ - angle ABC = 180^circ - 90^circ = 90^circ.
 - Góc tại đỉnh B của hình bình hành BPCD là angle CBP. Tuy nhiên, thứ tự đỉnh là B-P-C-D. Góc tại B là angle DBP hoặc angle CBP. Nếu đỉnh là B, P, C, D thì góc tại B là angle DBP.
 - Từ A-B-P thẳng hàng, ta có angle ABC = 90^circ.
 - Góc angle DBC là một phần của angle ABC.
 - Góc angle ABC = angle ABD + angle DBC = 90^circ.
 - Do angle ABD = 45^circ, suy ra angle DBC = 90^circ - 45^circ = 45^circ.
 - Bây giờ xét góc tại B của BPCD, đó là angle DBP.
 - Vì A-B-P thẳng hàng, góc angle DBP là góc kề bù với angle ABD.
 - angle DBP = 180^circ - angle ABD = 180^circ - 45^circ = 135^circ.
 - Vì BPCD là hình bình hành, các góc đối bằng nhau: angle DBP = angle PCD = 135^circ.
 - Các góc kề bù: angle BPC + angle PCD = 180^circ => angle BPC = 180^circ - 135^circ = 45^circ.
 - Vậy các góc của BPCD là 135^circ, 45^circ, 135^circ, 45^circ.
- Kết luận cuối cùng cho phần b:
 - Góc tại B của BPCD là angle DBP = 135^circ.
 - Góc tại P của BPCD là angle BPC = 45^circ.
 - Góc tại C của BPCD là angle PCD = 135^circ.
 - Góc tại D của BPCD là angle CDB = 45^circ.
Mẹo kiểm tra: Vẽ hình cẩn thận với các giả thiết. Kiểm tra xem góc đang tính là góc nào và mối quan hệ của nó với các góc đã biết.
Lỗi hay gặp: Nhầm lẫn vị trí các điểm trên tia, nhầm lẫn góc kề bù, góc so le trong, góc đồng vị, hoặc áp dụng sai tính chất của hình bình hành.

Đáp Án/Kết Quả

Bài 3.39: Khẳng định B là đúng. Các khẳng định A, C, D sai.

Bài 3.40:

a) Sai.
b) Sai.
c) Đúng.
d) Sai.

Bài 3.41:

a) Đúng.
b) Đúng.
c) Đúng.
d) Sai.

Bài 3.42: Chứng minh tứ giác ABCD là hình thang cân dựa trên hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau bằng cách chứng minh AB // CD và AC = BD.

Bài 3.43:

a) Tứ giác BPCD là hình bình hành.
b) Các góc của tứ giác BPCD là 135^circ, 45^circ, 135^circ, 45^circ. Cụ thể: angle DBP = 135^circ, angle BPC = 45^circ, angle PCD = 135^circ, angle CDB = 45^circ.

Conclusion

Bài viết đã cung cấp lời giải chi tiết và phân tích kỹ lưỡng cho các bài tập thuộc chủ đề Giải Toán 8 trang 74 Tập 1 trong bộ sách Kết nối tri thức. Việc nắm vững các định nghĩa, tính chất và dấu hiệu nhận biết các loại tứ giác đặc biệt, kết hợp với kỹ năng chứng minh hình học, sẽ giúp học sinh tự tin chinh phục các dạng bài tập tương tự.

Ngày chỉnh sửa nội dung mới nhất January 8, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.