Giải Toán Lớp 7 Trang 98, 99 Tập 2 Sách Kết Nối Tri Thức: Hình Lăng Trụ Đứng Tam Giác và Tứ Giác

Chào mừng các em đến với tài liệu giải toán hình lớp 7 tập 2, tập trung vào chủ đề hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác theo sách Kết Nối Tri Thức. Bài viết này cung cấp lời giải chi tiết cho các bài tập từ 10.11 đến 10.16, giúp các em nắm vững kiến thức và phương pháp giải. Bên cạnh đó, chúng ta sẽ cùng nhau xem xét các công thức toán học liên quan để giải quyết bài tập một cách hiệu quả nhất.

Đề Bài

Bài 10.11 Trang 98 SGK Toán Lớp 7

Quan sát và gọi tên các mặt đáy, mặt bên, cạnh đáy, cạnh bên của hình lăng trụ đứng tam giác ở hình 10.31.

Bài 10.12 Trang 99 SGK Toán Lớp 7

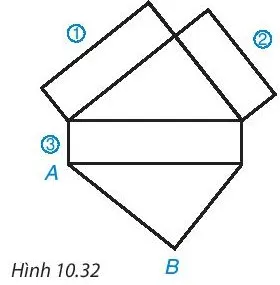
Quan sát Hình 10.12 và cho biết cạnh nào trong các cạnh (1), (2), (3) ghép với cạnh AB để có hình lăng trụ đứng.

giai toan lop 7 trang 98 99 tap 2 sach ket noi tri thuc 2

Bài 10.13 Trang 99 SGK Toán Lớp 7

Tính diện tích xung quanh và thể tích hình lăng trụ đứng trong hình 10.33.

giai toan lop 7 trang 98 99 tap 2 sach ket noi tri thuc 3

Bài 10.14 Trang 99 SGK Toán Lớp 7

Thùng một chiếc máy nông nghiệp có dạng hình lăng trụ đứng tứ giác như hình 10.34. Đáy của hình lăng trụ đứng này (mặt bên của thùng) là một hình thang vuông có độ dài đáy lớn 3 m, đáy nhỏ 1,5 m. Hỏi thùng có dung tích bao nhiêu mét khối ?

giai toan lop 7 trang 98 99 tap 2 sach ket noi tri thuc 5

Bài 10.15 Trang 99 SGK Toán Lớp 7

Một hình gồm hai lăng trụ đứng ghép lại với các kích thước như ở hình 10.35. Tính thể tích hình ghép.

giai toan lop 7 trang 98 99 tap 2 sach ket noi tri thuc 8

Bài 10.16 Trang 99 SGK Toán Lớp 7

Một hộp đựng khẩu trang y tế được làm bằng bìa cứng có dạng một hình hộp chữ nhật, kích thước như hình 10.36.
a) Hãy tính thể tích của hộp.
b) Tính diện tích bìa cứng dùng để làm hộp (bỏ qua mép dán).

giai toan lop 7 trang 98 99 tap 2 sach ket noi tri thuc 11

Phân Tích Yêu Cầu

Các bài tập từ 10.11 đến 10.16 đều xoay quanh khái niệm về hình lăng trụ đứng, bao gồm cả hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác (hình hộp chữ nhật, lăng trụ đứng có đáy là hình thang). Yêu cầu chung là nhận biết các yếu tố của hình, xác định các cạnh phù hợp để tạo thành hình lăng trụ, tính toán diện tích xung quanh, thể tích và diện tích bìa cứng để làm hộp.

Chúng ta cần phân biệt rõ mặt đáy, mặt bên, cạnh đáy và cạnh bên của hình lăng trụ. Khi tính toán, việc áp dụng đúng công thức diện tích xung quanh và thể tích là yếu tố then chốt. Đối với các hình ghép, ta cần chia nhỏ thành các hình cơ bản đã biết cách tính.

Kiến Thức/Nền Tảng Cần Dùng

Để giải quyết các bài toán này, chúng ta cần nắm vững các khái niệm và công thức sau:

1. Hình lăng trụ đứng

• Mặt đáy: Hai mặt song song và bằng nhau. Trong hình lăng trụ đứng tam giác, mặt đáy là tam giác. Trong hình lăng trụ đứng tứ giác, mặt đáy có thể là hình chữ nhật, hình vuông, hình thang, hình bình hành.
• Mặt bên: Các mặt là hình chữ nhật (hoặc hình vuông).
• Cạnh đáy: Các cạnh của mặt đáy.
• Cạnh bên: Các đoạn thẳng nối hai đỉnh tương ứng của hai mặt đáy. Trong hình lăng trụ đứng, các cạnh bên vuông góc với mặt đáy và có độ dài bằng nhau.

2. Công thức tính diện tích xung quanh của hình lăng trụ đứng

Diện tích xung quanh của hình lăng trụ đứng bằng chu vi đáy nhân với chiều cao.
Công thức: S_xq = P_đáy times h
Trong đó:

• S_xq là diện tích xung quanh.
• P_đáy là chu vi của mặt đáy.
• h là chiều cao của hình lăng trụ đứng (chính là độ dài cạnh bên).

3. Công thức tính thể tích của hình lăng trụ đứng

Thể tích của hình lăng trụ đứng bằng diện tích đáy nhân với chiều cao.
Công thức: V = S_đáy times h
Trong đó:

• V là thể tích.
• S_đáy là diện tích của một mặt đáy.
• h là chiều cao của hình lăng trụ đứng.

4. Công thức tính diện tích hình phẳng cơ bản

• Diện tích hình tam giác: S = frac{1}{2} times text{đáy} times text{chiều cao}
• Diện tích hình chữ nhật: S = text{chiều dài} times text{chiều rộng}
• Diện tích hình thang: S = frac{1}{2} times (text{đáy lớn} + text{đáy nhỏ}) times text{chiều cao}

Hướng Dẫn Giải Chi Tiết

Giải Bài 10.11 Trang 98 SGK Toán Lớp 7

Để xác định các yếu tố của hình lăng trụ đứng tam giác (Hình 10.31), chúng ta cần quan sát cẩn thận cấu trúc của nó.

• Mặt đáy: Hình lăng trụ đứng tam giác có hai mặt đáy là hai tam giác song song và bằng nhau. Dựa vào hình, hai mặt đáy đó là tam giác ABC và tam giác MNP.
• Mặt bên: Hình lăng trụ đứng có các mặt bên là hình chữ nhật. Với hình lăng trụ đứng tam giác có đáy ABC và MNP, các mặt bên sẽ được tạo thành từ các cạnh của đáy và các cạnh bên. Đó là các hình ACPM, BAMN, BCPN.
• Cạnh đáy: Đây là các cạnh thuộc hai mặt đáy. Chúng bao gồm các cạnh của tam giác ABC (AB, BC, CA) và các cạnh tương ứng của tam giác MNP (MN, NP, PM).
• Cạnh bên: Đây là các đoạn thẳng nối các đỉnh tương ứng của hai mặt đáy. Trong hình này, các cạnh bên là AM, BN, CP.

Mẹo kiểm tra: Các cạnh bên phải song song với nhau và có độ dài bằng nhau. Mỗi mặt bên phải là hình chữ nhật.

Lỗi hay gặp: Nhầm lẫn giữa cạnh đáy và cạnh bên, hoặc xác định sai số lượng mặt bên.

Giải Bài 10.12 Trang 99 SGK Toán Lớp 7

Bài toán yêu cầu xác định cạnh nào trong số (1), (2), (3) khi ghép với cạnh AB sẽ tạo thành hình lăng trụ đứng. Đặc điểm quan trọng của hình lăng trụ đứng là các cạnh bên phải có độ dài bằng nhau và song song với nhau. Nếu AB là một cạnh đáy, thì cạnh tương ứng trên mặt đáy còn lại phải có cùng độ dài.

Quan sát hình 10.12, ta thấy AB là một cạnh của mặt đáy. Cạnh tương ứng trên mặt đáy còn lại cần phải có độ dài bằng AB để tạo thành cạnh bên nối hai mặt đáy.

• Cạnh (1) có cùng độ dài với AB.
• Cạnh (2) và (3) có độ dài khác AB.

Do đó, cạnh (1) khi ghép với AB sẽ tạo thành một cạnh bên, và nếu các điều kiện khác được thỏa mãn, nó sẽ tạo thành hình lăng trụ đứng.

Đáp án: Cạnh số (1) ghép với cạnh AB để có hình lăng trụ đứng.

Mẹo kiểm tra: Trong hình lăng trụ đứng, tất cả các cạnh bên đều phải bằng nhau. Nếu AB là cạnh đáy, thì cạnh tương ứng ở đáy kia phải bằng AB.

Lỗi hay gặp: Chọn nhầm cạnh có độ dài không phù hợp hoặc không hiểu mối quan hệ giữa các cạnh trong hình lăng trụ.

Giải Bài 10.13 Trang 99 SGK Toán Lớp 7

Để tính diện tích xung quanh và thể tích hình lăng trụ đứng cho trong hình 10.33, chúng ta cần xác định rõ các yếu tố của hình: mặt đáy, chiều cao và chu vi đáy.

Hình 10.33 mô tả một hình lăng trụ đứng có đáy là tam giác vuông.

• Các cạnh đáy của tam giác là 3 cm, 4 cm và 5 cm (vì đây là tam giác vuông, cạnh huyền là cạnh lớn nhất 5 cm).
• Chiều cao của hình lăng trụ là 7 cm.

Bước 1: Tính chu vi đáy
Chu vi đáy P_đáy là tổng độ dài ba cạnh của tam giác đáy:
P_đáy = 3 + 4 + 5 = 12 cm.

Bước 2: Tính diện tích xung quanh
Áp dụng công thức S_xq = P_đáy times h:
S_xq = 12 text{ cm} times 7 text{ cm} = 84 cm^2.

Bước 3: Tính diện tích đáy
Mặt đáy là một tam giác vuông có hai cạnh góc vuông là 3 cm và 4 cm.
Diện tích đáy S_đáy được tính bằng công thức diện tích tam giác vuông:
S_đáy = frac{1}{2} times text{cạnh góc vuông 1} times text{cạnh góc vuông 2}
S_đáy = frac{1}{2} times 3 text{ cm} times 4 text{ cm} = frac{1}{2} times 12 text{ cm}^2 = 6 cm^2.

Bước 4: Tính thể tích
Áp dụng công thức V = S_đáy times h:
V = 6 text{ cm}^2 times 7 text{ cm} = 42 cm^3.

Đáp án:

• Diện tích xung quanh: 84 cm^2.
• Thể tích: 42 cm^3.

Mẹo kiểm tra: Đơn vị của diện tích xung quanh là cm^2, đơn vị thể tích là cm^3, điều này là chính xác. Kiểm tra lại phép cộng chu vi và phép nhân diện tích, thể tích.

Lỗi hay gặp: Nhầm lẫn công thức diện tích xung quanh và thể tích, sử dụng sai độ dài cạnh đáy hoặc chiều cao, tính sai diện tích tam giác vuông.

Giải Bài 10.14 Trang 99 SGK Toán Lớp 7

Bài toán này yêu cầu tính dung tích (tức là thể tích) của một thùng máy nông nghiệp có dạng hình lăng trụ đứng tứ giác. Đáy của hình lăng trụ này là một hình thang vuông.

Cho biết:

• Đáy lớn của hình thang: 3 m.
• Đáy nhỏ của hình thang: 1,5 m.
• Chiều cao của hình lăng trụ đứng (chiều cao của thùng): Chúng ta cần xác định chiều cao này từ hình 10.34. Chiều cao của hình lăng trụ được cho là 2 m.

Bước 1: Tính diện tích mặt đáy
Mặt đáy là hình thang vuông. Áp dụng công thức tính diện tích hình thang:
S_đáy = frac{1}{2} times (text{đáy lớn} + text{đáy nhỏ}) times text{chiều cao hình thang}
Trong hình 10.34, chiều cao của hình thang đáy chính là cạnh vuông góc với hai đáy, có độ dài là 2 m (cùng với chiều cao của lăng trụ).
S_đáy = frac{1}{2} times (3 text{ m} + 1,5 text{ m}) times 2 text{ m}
S_đáy = frac{1}{2} times 4,5 text{ m} times 2 text{ m}
S_đáy = 4,5 m^2.

Bước 2: Tính thể tích thùng
Áp dụng công thức tính thể tích hình lăng trụ đứng: V = S_đáy times h.
Ở đây, h là chiều cao của hình lăng trụ đứng (chiều cao của thùng), được cho là 1 m trong hình vẽ. Tuy nhiên, hình vẽ cho thấy cạnh bên có độ dài là 1m, và chiều cao của hình thang đáy là 2m. Cần làm rõ chiều cao của lăng trụ. Dựa vào hình ảnh, chiều cao của hình thang là 2m và chiều cao của lăng trụ là 1m.

Kiểm tra lại dữ liệu từ hình:

• Đáy lớn hình thang: 3 m
• Đáy nhỏ hình thang: 1,5 m
• Chiều cao hình thang (cạnh vuông góc với đáy lớn và nhỏ): 2 m
• Chiều cao của hình lăng trụ đứng (cạnh bên): 1 m

Tính lại diện tích đáy với chiều cao hình thang là 2m:
S_đáy = frac{1}{2} times (3 + 1,5) times 2 = frac{1}{2} times 4,5 times 2 = 4,5 m^2.

Tính thể tích hình lăng trụ với chiều cao h = 1 m:
V = S_đáy times h = 4,5 text{ m}^2 times 1 text{ m} = 4,5 m^3.

Đáp án: Thùng có dung tích là 4,5 mét khối.

Mẹo kiểm tra: Đảm bảo đã phân biệt rõ chiều cao của hình thang đáy và chiều cao của hình lăng trụ. Đơn vị thể tích là mét khối (m^3), phù hợp với đơn vị đo chiều dài là mét (m).

Lỗi hay gặp: Nhầm lẫn giữa chiều cao của mặt đáy (hình thang) và chiều cao của hình lăng trụ. Tính sai diện tích hình thang.

Giải Bài 10.15 Trang 99 SGK Toán Lớp 7

Bài toán yêu cầu tính thể tích của một hình được ghép từ hai hình lăng trụ đứng. Dựa vào hình 10.35, ta có thể thấy hình này được ghép từ một hình lăng trụ đứng tam giác và một hình lăng trụ đứng tứ giác (hình chữ nhật).

Chúng ta cần tính thể tích của từng hình lăng trụ rồi cộng lại.

Phân tích hình:
Hình lăng trụ đứng tam giác:

• Cạnh đáy: 3 cm, 4 cm, 5 cm (tam giác vuông).
• Chiều cao của lăng trụ: 6 cm.

Hình lăng trụ đứng tứ giác (hình hộp chữ nhật):

• Kích thước mặt đáy: 2 cm x 4 cm.
• Chiều cao của lăng trụ: 6 cm.

Bước 1: Tính thể tích hình lăng trụ đứng tam giác

• Diện tích đáy (tam giác vuông): S_đáy_tam_giac = frac{1}{2} times 3 text{ cm} times 4 text{ cm} = 6 cm^2.
• Chiều cao lăng trụ: h_1 = 6 cm.
• Thể tích lăng trụ tam giác: V_1 = S_đáy_tam_giac times h_1 = 6 text{ cm}^2 times 6 text{ cm} = 36 cm^3.

Bước 2: Tính thể tích hình lăng trụ đứng tứ giác (hình hộp chữ nhật)

• Diện tích đáy (hình chữ nhật): S_đáy_chu_nhat = 2 text{ cm} times 4 text{ cm} = 8 cm^2.
• Chiều cao lăng trụ: h_2 = 6 cm.
• Thể tích lăng trụ tứ giác: V_2 = S_đáy_chu_nhat times h_2 = 8 text{ cm}^2 times 6 text{ cm} = 48 cm^3.

Bước 3: Tính thể tích hình ghép
Thể tích của hình ghép là tổng thể tích của hai hình lăng trụ:
V_{ghép} = V_1 + V_2 = 36 text{ cm}^3 + 48 text{ cm}^3 = 84 cm^3.

Đáp án: Thể tích hình ghép là 84 cm^3.

Mẹo kiểm tra: Xác định đúng các thành phần của hai hình lăng trụ (đáy, chiều cao) và áp dụng đúng công thức. Phép cộng thể tích phải chính xác.

Lỗi hay gặp: Nhầm lẫn kích thước của hình này với hình kia, tính sai diện tích đáy, áp dụng sai công thức thể tích.

Giải Bài 10.16 Trang 99 SGK Toán Lớp 7

Bài toán yêu cầu tính thể tích và diện tích bìa cứng để làm một hộp đựng khẩu trang y tế có dạng hình hộp chữ nhật, với các kích thước cho trên hình 10.36.

Cho biết kích thước hộp:

• Chiều dài: 10 cm
• Chiều rộng: 8 cm
• Chiều cao: 7 cm

a) Tính thể tích của hộp
Hình hộp chữ nhật là một dạng đặc biệt của hình lăng trụ đứng tứ giác. Công thức tính thể tích hình hộp chữ nhật là:
V = text{chiều dài} times text{chiều rộng} times text{chiều cao}
V = 10 text{ cm} times 8 text{ cm} times 7 text{ cm}
V = 80 text{ cm}^2 times 7 text{ cm}
V = 560 cm^3.

b) Tính diện tích bìa cứng dùng để làm hộp
Diện tích bìa cứng chính là diện tích toàn phần của hình hộp chữ nhật. Công thức tính diện tích toàn phần của hình hộp chữ nhật là:
S_{tp} = 2 times (text{chiều dài} times text{chiều rộng} + text{chiều dài} times text{chiều cao} + text{chiều rộng} times text{chiều cao})
S_{tp} = 2 times (10 times 8 + 10 times 7 + 8 times 7) cm^2
S_{tp} = 2 times (80 + 70 + 56) cm^2
S_{tp} = 2 times (150 + 56) cm^2
S_{tp} = 2 times 206 cm^2
S_{tp} = 412 cm^2.

Một cách tính khác là diện tích xung quanh cộng với diện tích hai đáy:

• Diện tích xung quanh: S_{xq} = P_{đáy} times h = (2 times (10+8)) times 7 = (2 times 18) times 7 = 36 times 7 = 252 cm^2.
• Diện tích hai đáy: S_{2 đáy} = 2 times (10 times 8) = 2 times 80 = 160 cm^2.
• Diện tích toàn phần: S_{tp} = S_{xq} + S_{2 đáy} = 252 + 160 = 412 cm^2.

Đáp án:
a) Thể tích của hộp là 560 cm^3.
b) Diện tích bìa cứng dùng để làm hộp là 412 cm^2.

Mẹo kiểm tra: Đơn vị thể tích là cm^3, đơn vị diện tích là cm^2. Phép tính cộng và nhân phải được thực hiện cẩn thận.

Lỗi hay gặp: Nhầm lẫn giữa công thức thể tích và diện tích toàn phần, tính sai diện tích của các mặt hình chữ nhật hoặc chu vi đáy.

Đáp Án/Kết Quả

Dưới đây là tóm tắt các kết quả cho từng bài tập:

• Bài 10.11:
  • 2 mặt đáy: ABC, MNP.
  • 3 mặt bên: ACPM, BAMN, BCPN.
  • Cạnh đáy: NM, MP, NP, AB, BC, CA.
  • Cạnh bên: AM, BN, CP.
• Bài 10.12: Cạnh số (1) ghép với cạnh AB để có hình lăng trụ đứng.
• Bài 10.13: Diện tích xung quanh: 84 cm^2; Thể tích: 42 cm^3.
• Bài 10.14: Dung tích thùng: 4,5 m^3.
• Bài 10.15: Thể tích hình ghép: 84 cm^3.
• Bài 10.16:
  • a) Thể tích hộp: 560 cm^3.
  • b) Diện tích bìa cứng: 412 cm^2.

Conclusion

Qua việc giải chi tiết các bài tập từ 10.11 đến 10.16, chúng ta đã ôn tập và củng cố kiến thức về hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác trong chương trình giải toán hình lớp 7 tập 2. Việc nắm vững các khái niệm cơ bản, phân biệt rõ các yếu tố của hình và áp dụng chính xác các công thức tính diện tích xung quanh, thể tích sẽ giúp các em tự tin chinh phục các dạng bài tập tương tự. Hãy ghi nhớ phương pháp và thực hành thêm để làm chủ kiến thức này.

Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.