Hướng Dẫn Giải Bài 2 Trang 88 Toán Lớp 6 Tập 1 Cánh Diều Chi Tiết Nhất

by Thầy Đông · January 7, 2026

Rate this post

Giải toán lớp 6 tập 1 bài 2 là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về số nguyên âm, số nguyên dương và cách xác định khoảng cách trên trục số. Bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu, đồng thời phân tích kỹ lưỡng từng bước để các em có thể nắm vững phương pháp giải.

Đề Bài

Trong Hình 10, hãy tính (theo mét):
a) Khoảng cách giữa rặng san hô và người thợ lặn;
b) Khoảng cách giữa người thợ lặn và mặt nước;
c) Khoảng cách giữa mặt nước và con chim;
d) Khoảng cách giữa rặng san hô và con chim.

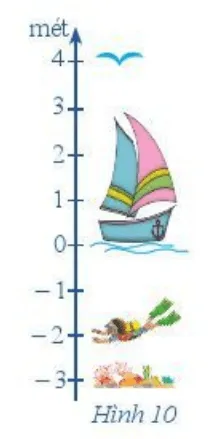Hình 10 minh họa bài toán

Phân Tích Yêu Cầu

Bài toán yêu cầu chúng ta tính toán khoảng cách giữa các đối tượng khác nhau (rặng san hô, người thợ lặn, mặt nước, con chim) dựa trên thông tin vị trí của chúng được biểu thị trên một trục số thẳng đứng hoặc thang đo độ sâu. Dữ liệu quan trọng nhất là vị trí tương ứng của mỗi đối tượng trên trục mét.

Để giải bài toán này, chúng ta cần hiểu rằng khoảng cách giữa hai điểm trên một trục số được tính bằng hiệu của hai số đó (lấy số lớn trừ số bé) hoặc bằng giá trị tuyệt đối của hiệu đó.

Kiến Thức/Nền Tảng Cần Dùng

Để giải quyết bài toán này, chúng ta cần nắm vững các khái niệm sau:

Số nguyên âm và số nguyên dương: Số nguyên âm là các số nhỏ hơn 0 (ký hiệu bằng dấu “-“), thường dùng để chỉ độ sâu dưới mặt nước. Số nguyên dương là các số lớn hơn 0 (có thể viết kèm dấu “+” hoặc không), thường dùng để chỉ độ cao so với mặt nước hoặc các vị trí trên mặt nước. Số 0 biểu thị cho mặt nước.
Trục số: Một đường thẳng trên đó các số được biểu diễn theo một thứ tự nhất định, thường là từ trái sang phải hoặc từ dưới lên trên. Trong bài toán này, trục số được dùng để biểu diễn độ sâu và độ cao so với mặt nước.
Tính khoảng cách trên trục số: Khoảng cách giữa hai điểm (a) và (b) trên trục số được tính bằng (|a – b|) hoặc bằng cách lấy giá trị lớn hơn trừ đi giá trị nhỏ hơn.

Cụ thể, các công thức và quy tắc sau đây sẽ được áp dụng:

Khoảng cách giữa hai số nguyên (x) và (y) là (|x – y|).
Nếu (x > y), khoảng cách là (x – y).
Nếu (y > x), khoảng cách là (y – x).

Hướng Dẫn Giải Chi Tiết

Dựa vào Hình 10 và các thông tin được cung cấp, chúng ta xác định vị trí của từng đối tượng trên trục mét như sau:

Rặng san hô: Tương ứng với vị trí – 3 m.
Người thợ lặn: Tương ứng với vị trí – 2 m.
Mặt nước: Tương ứng với vị trí 0 m.
Con chim: Tương ứng với vị trí 4 m.

Bây giờ, chúng ta sẽ tiến hành tính toán khoảng cách cho từng câu hỏi:

a) Khoảng cách giữa rặng san hô và người thợ lặn

Vị trí rặng san hô: – 3 m
Vị trí người thợ lặn: – 2 m

Vì – 2 > – 3, ta lấy vị trí người thợ lặn trừ đi vị trí rặng san hô.
Khoảng cách = ( |(-2) – (-3)| )
Khoảng cách = ( |-2 + 3| )
Khoảng cách = ( |1| )
Khoảng cách = 1 (m)

Hoặc có thể hiểu: Người thợ lặn ở – 2m, rặng san hô ở – 3m. Khoảng cách giữa hai điểm này là 1 mét.

b) Khoảng cách giữa người thợ lặn và mặt nước

Vị trí người thợ lặn: – 2 m
Vị trí mặt nước: 0 m

Vì 0 > – 2, ta lấy vị trí mặt nước trừ đi vị trí người thợ lặn.
Khoảng cách = ( |0 – (-2)| )
Khoảng cách = ( |0 + 2| )
Khoảng cách = ( |2| )
Khoảng cách = 2 (m)

Điều này có nghĩa là người thợ lặn đang ở độ sâu 2 mét dưới mặt nước.

c) Khoảng cách giữa mặt nước và con chim

Vị trí mặt nước: 0 m
Vị trí con chim: 4 m

Vì 4 > 0, ta lấy vị trí con chim trừ đi vị trí mặt nước.
Khoảng cách = ( |4 – 0| )
Khoảng cách = ( |4| )
Khoảng cách = 4 (m)

Con chim đang ở độ cao 4 mét so với mặt nước.

d) Khoảng cách giữa rặng san hô và con chim

Vị trí rặng san hô: – 3 m
Vị trí con chim: 4 m

Vì 4 > – 3, ta lấy vị trí con chim trừ đi vị trí rặng san hô.
Khoảng cách = ( |4 – (-3)| )
Khoảng cách = ( |4 + 3| )
Khoảng cách = ( |7| )
Khoảng cách = 7 (m)

Khoảng cách này là tổng quãng đường từ rặng san hô dưới đáy lên tới mặt nước rồi bay lên cao.

Mẹo kiểm tra

Để kiểm tra kết quả, bạn có thể hình dung trục số:

Khoảng cách từ – 3 lên – 2 là 1 đơn vị.
Khoảng cách từ – 2 lên 0 (mặt nước) là 2 đơn vị.
Khoảng cách từ 0 lên 4 (con chim) là 4 đơn vị.
Tổng các khoảng cách này sẽ cho thấy sự chính xác. Ví dụ, khoảng cách từ rặng san hô (– 3) đến con chim (4) là khoảng cách từ – 3 đến 0 cộng với khoảng cách từ 0 đến 4, tức là 3 + 4 = 7 (m), khớp với kết quả tính toán.

Lỗi hay gặp

Một lỗi phổ biến khi làm bài toán này là nhầm lẫn giữa số âm và số dương, hoặc không xác định đúng số nào lớn hơn số nào để thực hiện phép trừ. Cần chú ý rằng trên trục số, các số âm càng lớn về giá trị tuyệt đối thì càng nhỏ (ví dụ: – 3 < – 2).

Đáp Án/Kết Quả

Dựa trên phân tích và tính toán, đáp án cho bài 2 trang 88 Toán lớp 6 Tập 1 Cánh diều như sau:

a) Khoảng cách giữa rặng san hô và người thợ lặn là 1 mét.
b) Khoảng cách giữa người thợ lặn và mặt nước là 2 mét.
c) Khoảng cách giữa mặt nước và con chim là 4 mét.
d) Khoảng cách giữa rặng san hô và con chim là 7 mét.

Hy vọng với phần hướng dẫn chi tiết này, các em học sinh sẽ nắm vững cách giải bài toán liên quan đến số nguyên trên trục số.

Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.