Giải Toán Lớp 6 Tập 2 Trang 58 Sách Chân Trời Sáng Tạo Chuẩn KaTeX

Trong chương trình học Toán lớp 6, việc nắm vững các khái niệm về đối xứng là vô cùng quan trọng. Bài viết này sẽ cung cấp lời giải chi tiết và chuẩn xác cho các bài tập trang 58, Tập 2, sách giải toán lớp 6 tập 2 trang 58 thuộc bộ sách Chân Trời Sáng Tạo, giúp các em học sinh dễ dàng tiếp thu kiến thức về tâm đối xứng.

Đề Bài

Bài 1 trang 58 Toán lớp 6 Tập 2:

Hãy tìm tâm đối xứng của các hình sau đây (nếu có).

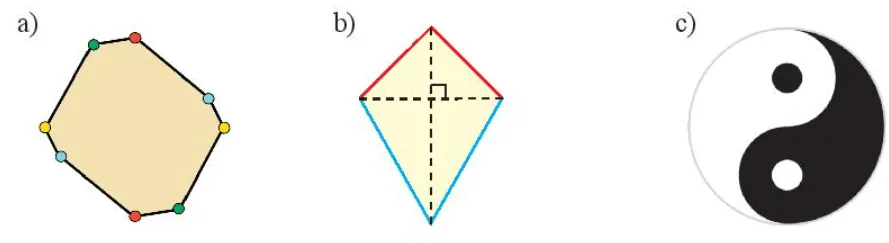Hãy tìm tâm đối xứng của các hình sau đây (nếu có)

Bài 2 trang 58 Toán lớp 6 Tập 2:

Hình nào sau đây có tâm đối xứng? Hãy chỉ ra tâm đối xứng của nó (nếu có).

Hình nào sau đây có tâm đối xứng? Hãy chỉ ra tâm đối xứng của nó (nếu có)

Bài 3 trang 58 Toán lớp 6 Tập 2:

Chữ cái nào sau đây có tâm đối xứng? Chữ cái nào vừa có trục đối xứng, vừa có tâm đối xứng?

Chữ cái nào sau đây có tâm đối xứng? Chữ cái nào vừa có trục đối

Bài 4 trang 58 Toán lớp 6 Tập 2:

Hình nào sau đây có tâm đối xứng?

Hình nào sau đây có tâm đối xứng?

Phân Tích Yêu Cầu

Các bài tập này yêu cầu xác định tâm đối xứng của các hình cho trước, bao gồm hình học đơn giản và các chữ cái. Chúng ta cần áp dụng định nghĩa về tâm đối xứng để phân tích từng hình. Một hình có tâm đối xứng nếu có một điểm mà khi quay hình đó 180 độ quanh điểm đó, hình không thay đổi vị trí. Điểm đó được gọi là tâm đối xứng.

Kiến Thức/Nền Tảng Cần Dùng

Định nghĩa tâm đối xứng

Điểm O được gọi là tâm đối xứng của hình H nếu phép quay tâm O với góc 180 độ biến mỗi điểm thuộc hình H thành một điểm thuộc hình H. Nói cách khác, nếu điểm A thuộc hình H thì điểm A’ đối xứng với A qua O cũng thuộc hình H.

Các hình có tâm đối xứng thường gặp

• Hình chữ nhật: Có tâm đối xứng là giao điểm hai đường chéo.
• Hình bình hành: Có tâm đối xứng là giao điểm hai đường chéo.
• Hình vuông: Có tâm đối xứng là giao điểm hai đường chéo (cũng là tâm đối xứng của hình chữ nhật và hình thoi).
• Đường tròn: Tâm đường tròn là tâm đối xứng của nó.
• Đoạn thẳng: Trung điểm của đoạn thẳng là tâm đối xứng của nó.
• Tam giác đều: Không có tâm đối xứng.
• Tam giác cân: Không có tâm đối xứng.
• Tam giác vuông: Không có tâm đối xứng.

Chữ cái có tâm đối xứng

Một số chữ cái in hoa trong bảng chữ cái Latinh có tâm đối xứng khi xét theo hình dạng tiêu chuẩn:

• Chữ có cả trục đối xứng và tâm đối xứng: I, O.
• Chữ chỉ có tâm đối xứng (không có trục đối xứng): H, N, S, Z, X.

Hướng Dẫn Giải Chi Tiết

Bài 1 trang 58: Tìm tâm đối xứng của các hình

• Hình a): Hình này là một hình bình hành. Tâm đối xứng của hình bình hành là giao điểm hai đường chéo của nó. Dựa vào hình vẽ, ta thấy điểm được đánh dấu là tâm đối xứng.
• Hình b): Hình này có dạng giống một mũi tên hoặc một hình tam giác có phần mở rộng. Khi xoay 180 độ quanh bất kỳ điểm nào, hình sẽ không trùng lại với chính nó. Do đó, hình này không có tâm đối xứng.
• Hình c): Xét về mặt hình học thuần túy (không kể màu sắc), hình này có một điểm trung tâm mà phép quay 180 độ quanh đó sẽ làm hình trùng lại với chính nó. Tuy nhiên, nếu xét cả màu sắc, nó có thể không có tâm đối xứng. Theo hình vẽ minh họa, nếu chỉ xét hình dạng thì có tâm đối xứng.

Mẹo kiểm tra: Hãy thử đặt một cây bút chì hoặc que tăm vào điểm nghi ngờ là tâm đối xứng. Xoay nhẹ hình 180 độ. Nếu hình trùng khớp với ban đầu thì đó là tâm đối xứng.

Lỗi hay gặp: Nhầm lẫn giữa trục đối xứng và tâm đối xứng.

Hãy tìm tâm đối xứng của các hình sau đây (nếu có)Hãy tìm tâm đối xứng của các hình sau đây (nếu có)

Bài 2 trang 58: Hình nào có tâm đối xứng?

• Hình a): Nếu xét toàn bộ màu sắc, hình này không có tâm đối xứng. Tuy nhiên, nếu chỉ xét về mặt hình học, hình này có trục đối xứng đi qua tâm của hình tròn và vuông. Và nó cũng có tâm đối xứng tại chính giao điểm đó.
• Hình b): Hình này là một hình chữ nhật (hoặc hình vuông). Tâm đối xứng của hình chữ nhật/vuông là giao điểm hai đường chéo.
• Hình c): Hình này giống một chữ L hoặc một góc. Nó không có điểm nào mà phép quay 180 độ quanh đó làm hình trùng với chính nó. Do đó, hình này không có tâm đối xứng.

Hình nào sau đây có tâm đối xứng? Hãy chỉ ra tâm đối xứng của nó (nếu có)Hình nào sau đây có tâm đối xứng? Hãy chỉ ra tâm đối xứng của nó (nếu có)

Bài 3 trang 58: Chữ cái có tâm đối xứng và trục đối xứng

• Chữ cái có tâm đối xứng: Dựa trên hình dạng tiêu chuẩn của các chữ cái in hoa, các chữ cái có tâm đối xứng là: S, I, O, N. Khi xoay 180 độ quanh điểm giữa của chúng, hình dạng chữ cái không thay đổi.
• Chữ cái vừa có trục đối xứng, vừa có tâm đối xứng:
  • Chữ I: Có một trục đối xứng nằm ngang và một trục đối xứng nằm dọc. Giao điểm của hai trục này là tâm đối xứng.
  • Chữ O: Có vô số trục đối xứng (bất kỳ đường kính nào của đường tròn). Tâm của đường tròn là tâm đối xứng của chữ O.
    Các chữ cái như S, N chỉ có tâm đối xứng mà không có trục đối xứng.

Chữ cái nào sau đây có tâm đối xứng? Chữ cái nào vừa có trục đối

Bài 4 trang 58: Hình nào có tâm đối xứng?

• Hình thứ nhất: Hình này có dạng một ngôi sao 5 cánh hoặc một đa giác có nhiều điểm nhọn. Tuy nhiên, nếu xét kỹ, hình này có một điểm trung tâm mà phép quay 180 độ quanh đó làm hình trùng khớp. Do đó, nó có tâm đối xứng.
• Hình thứ hai: Hình này có dạng giống như một chiếc lá hoặc một hình không đều. Nó không có tâm đối xứng.
• Hình thứ ba: Hình này có dạng một đường cong không đối xứng hoặc một hình bất kỳ không có tính chất đối xứng qua một điểm. Nó không có tâm đối xứng.

Kết luận: Trong ba hình trên, chỉ có hình thứ nhất có tâm đối xứng.

Đáp Án/Kết Quả

• Bài 1: Hình a) và hình c) (nếu xét hình học) có tâm đối xứng. Hình b) không có.
• Bài 2: Hình a) (nếu xét hình học) và hình b) có tâm đối xứng. Hình c) không có.
• Bài 3:
  • Chữ cái có tâm đối xứng: S, I, O, N.
  • Chữ cái vừa có trục đối xứng, vừa có tâm đối xứng: I, O.
• Bài 4: Chỉ hình thứ nhất có tâm đối xứng.

Bài tập trang 58 sách giải toán lớp 6 tập 2 trang 58 Chân Trời Sáng Tạo đã giúp các em ôn lại và củng cố kiến thức về tâm đối xứng, một khái niệm quan trọng trong chương hình học.

Ngày chỉnh sửa nội dung mới nhất January 8, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.