Giải Toán Lớp 8 Trang 40 Sách Cánh Diều Tập 1: Phép Cộng, Phép Trừ Phân Thức Đại Số
Chào mừng các em đến với chuyên mục giải toán lớp 8 trang 40 sách Cánh Diều tập 1. Trong bài viết này, chúng ta sẽ cùng nhau chinh phục các bài tập liên quan đến phép cộng và phép trừ phân thức đại số. Bài viết cung cấp hướng dẫn chi tiết, phương pháp giải và đáp án chính xác, giúp các em nắm vững kiến thức nền tảng.
Đề Bài
Dưới đây là các bài tập được trích xuất từ sách giáo khoa Toán lớp 8 Cánh Diều tập 1, thuộc chủ đề phép cộng và phép trừ phân thức đại số.
Bài 1 (Trang 42): Thực hiện phép tính:
 Hình ảnh bài 1 trang 42
Hình ảnh bài 1 trang 42Bài 2 (Trang 42): Thực hiện phép tính:
 Hình ảnh bài 2 trang 42
Hình ảnh bài 2 trang 42Bài 3 (Trang 42): Thực hiện phép tính:
 Hình ảnh bài 3 trang 42
Hình ảnh bài 3 trang 42Bài 4 (Trang 43):
a) Rút gọn biểu thức:b) Tính giá trị của A tại x = -3
Bài 5 (Trang 43): Một xí nghiệp dự định sản xuất 10 000 sản phẩm trong x ngày. Khi thực hiện, xí nghiệp đã làm xong sớm hơn 1 ngày so với dự định và còn làm thêm được 80 sản phẩm. Viết phân thức biểu thị theo x:
a) Số sản phẩm xí nghiệp làm trong 1 ngày theo dự định;
b) Số sản phẩm xí nghiệp làm trong 1 ngày trên thực tế;
c) Số sản phẩm xí nghiệp làm trong 1 ngày trên thực tế nhiều hơn số sản phẩm xí nghiệp làm trong 1 ngày theo dự định.Bài 6 (Trang 43): Người ta mở hai vòi nước cùng chảy vào một bể không chứa nước. Thời gian để vòi thứ nhất chảy một mình đầy bể ít hơn thời gian để vòi thứ hai chảy một mình đầy bể là 2 giờ. Gọi x (giờ) là thời gian vòi thứ nhất chảy một mình để đầy bể. Viết phân thức biểu thị theo x:
a) Thời gian vòi thứ hai chảy một mình để đầy bể,
b) Phần bể mà mỗi vòi chảy được trong 1 giờ;
c) Phần bể mà cả hai vòi chảy được trong 1 giờ.Bài 7 (Trang 43): Để hưởng ứng phong trào Tết trồng cây, chi đoàn thanh niên dự định trồng 120 cây xanh. Khi bắt đầu thực hiện, chi đoàn được tăng cường thêm 3 đoàn viên. Gọi x là số đoàn viên ban đầu của chi đoàn và giả sử số cây mỗi đoàn viên trồng là như nhau. Viết phân thức biểu thị theo x:
a) Số cây mỗi đoàn viên trồng theo dự định;
b) Số cây mỗi đoàn viên trồng theo thực tế;
c) Số cây mỗi đoàn viên trồng theo dự định nhiều hơn số cây mỗi đoàn viên trồng theo thực tế.Bài 8 (Trang 43): Gia đình cô Lương nuôi ba con lợn con. Cả ba con lợn đều ăn cùng một loại thức ăn gia súc. Biểu đồ cột ở hình biểu diễn số ngày mà mỗi con lợn ăn hết một bao thức ăn. Hỏi cả ba con lợn ăn trong x ngày?
 Hình ảnh bài 8 trang 43
Hình ảnh bài 8 trang 43
Phân Tích Yêu Cầu
Các bài tập từ trang 42 và 43 sách Toán lớp 8 Cánh Diều tập 1 tập trung vào hai chủ đề chính: thực hiện phép cộng và phép trừ phân thức đại số, và ứng dụng các phép toán này vào giải các bài toán thực tế có liên quan đến năng suất, thời gian, công việc. Yêu cầu chung là thực hiện các phép tính với phân thức và thiết lập các biểu thức phân thức dựa trên các tình huống cụ thể.
Đối với các bài toán thực tế, chúng ta cần xác định rõ đại lượng cần tìm, các đại lượng đã cho, và mối quan hệ giữa chúng. Sau đó, thiết lập các phân thức tương ứng và sử dụng các quy tắc cộng, trừ phân thức để tìm ra biểu thức cuối cùng hoặc giá trị cần tính.
Kiến Thức/Nền Tảng Cần Dùng
Để giải quyết các bài tập này, chúng ta cần nắm vững các kiến thức sau:
- Định nghĩa phân thức đại số: Một phân thức đại số có dạng \frac{A}{B}, trong đó A và B là các đa thức, và B khác đa thức không.
- Quy tắc cộng, trừ phân thức cùng mẫu:
\frac{A}{M} + \frac{B}{M} = \frac{A+B}{M}
\frac{A}{M} - \frac{B}{M} = \frac{A-B}{M}
(với M khác đa thức không) - Quy tắc cộng, trừ phân thức khác mẫu: Để cộng hoặc trừ hai phân thức khác mẫu, ta quy đồng mẫu thức của chúng rồi áp dụng quy tắc cộng, trừ phân thức cùng mẫu.
- Phân thức đối: Phân thức đối của \frac{A}{B} là -\frac{A}{B} hoặc \frac{-A}{B}.
- Rút gọn phân thức: Chia cả tử và mẫu của phân thức cho nhân tử chung của chúng.
- Các bài toán thực tế liên quan đến năng suất: Nếu một công việc có thể hoàn thành trong $t$ giờ, thì trong 1 giờ, người ta hoàn thành \frac{1}{t} công việc đó.
Hướng Dẫn Giải Chi Tiết
Giải bài 1 – Bài 2 – Bài 3 (Trang 42)
Các bài toán này yêu cầu thực hiện phép cộng và phép trừ phân thức. Chúng ta sẽ áp dụng các quy tắc đã học.
Bài 1:
Các phân thức có cùng mẫu thức là x^2 - 1. Ta thực hiện phép cộng và trừ trực tiếp trên tử thức.
 Đáp án bài 1 trang 42
Đáp án bài 1 trang 42
Bài 2:
Tương tự, các phân thức có cùng mẫu thức là x^2 - 4. Ta thực hiện phép cộng và trừ.
 Đáp án bài 2 trang 42
Đáp án bài 2 trang 42 Đáp án bài 2 trang 42
Đáp án bài 2 trang 42
Bài 3:
Mẫu thức chung là x(x+1). Ta quy đồng mẫu thức để thực hiện phép trừ.
 Đáp án bài 3 trang 42
Đáp án bài 3 trang 42
- Mẹo kiểm tra: Sau khi thực hiện phép tính, hãy cố gắng rút gọn phân thức kết quả nếu có thể. Kiểm tra lại các bước quy đồng mẫu, nhân tử chung và các phép toán cộng trừ trên tử thức.
- Lỗi hay gặp: Sai sót trong quá trình đổi dấu khi trừ phân thức, hoặc sai sót khi quy đồng mẫu thức.
Giải bài 4 (Trang 43)
Đề bài:
a) Rút gọn biểu thức: \frac{x+1}{x(x+2)} - \frac{x-1}{x(x+2)}
b) Tính giá trị của A tại x = -3
Phương pháp giải:
a) Các phân thức có cùng mẫu thức là x(x+2). Ta thực hiện phép trừ trên tử thức, sau đó rút gọn.
b) Thay giá trị x = -3 vào biểu thức A đã rút gọn.
Đáp án:
a)
Biểu thức A có thể viết lại như sau:
A = \frac{x+1}{x(x+2)} - \frac{x-1}{x(x+2)}
A = \frac{(x+1) - (x-1)}{x(x+2)}
A = \frac{x+1 - x+1}{x(x+2)}
A = \frac{2}{x(x+2)}
b)
Với x = -3, ta thay vào biểu thức A đã rút gọn:
A = \frac{2}{(-3)(-3+2)} = \frac{2}{(-3)(-1)} = \frac{2}{3}
 Đáp án bài 4a trang 43
Đáp án bài 4a trang 43
Giải bài 5 (Trang 43)
Đề bài:
Một xí nghiệp dự định sản xuất 10 000 sản phẩm trong x ngày. Khi thực hiện, xí nghiệp đã làm xong sớm hơn 1 ngày so với dự định và còn làm thêm được 80 sản phẩm. Viết phân thức biểu thị theo x:
a) Số sản phẩm xí nghiệp làm trong 1 ngày theo dự định;
b) Số sản phẩm xí nghiệp làm trong 1 ngày trên thực tế;
c) Số sản phẩm xí nghiệp làm trong 1 ngày trên thực tế nhiều hơn số sản phẩm xí nghiệp làm trong 1 ngày theo dự định.
Phương pháp giải:
Số sản phẩm trong một ngày bằng tổng số sản phẩm chia cho số ngày.
Đáp án:
a) Theo dự định, xí nghiệp sản xuất 10 000 sản phẩm trong x ngày.
Số sản phẩm làm trong 1 ngày theo dự định là: \frac{10000}{x} (sản phẩm/ngày).
b) Thực tế, xí nghiệp làm xong sớm hơn 1 ngày, tức là trong x-1 ngày.
Tổng số sản phẩm làm được là 10000 + 80 = 10800 sản phẩm.
Số sản phẩm làm trong 1 ngày trên thực tế là: \frac{10800}{x-1} (sản phẩm/ngày).
c) Số sản phẩm làm trong 1 ngày trên thực tế nhiều hơn theo dự định là hiệu của hai đại lượng này:
\frac{10800}{x-1} - \frac{10000}{x}
Quy đồng mẫu thức: x(x-1).
= \frac{10800x - 10000(x-1)}{x(x-1)}
= \frac{10800x - 10000x + 10000}{x(x-1)}
= \frac{800x + 10000}{x(x-1)}
Giải bài 6 (Trang 43)
Đề bài:
Thời gian vòi thứ nhất chảy một mình đầy bể là $x$ giờ. Thời gian vòi thứ hai chảy một mình đầy bể ít hơn vòi thứ nhất là 2 giờ. Viết phân thức biểu thị theo $x$:
a) Thời gian vòi thứ hai chảy một mình để đầy bể,
b) Phần bể mà mỗi vòi chảy được trong 1 giờ;
c) Phần bể mà cả hai vòi chảy được trong 1 giờ.
Phương pháp giải:
Phần công việc hoàn thành trong 1 giờ bằng 1 chia cho tổng thời gian hoàn thành công việc đó.
Đáp án:
a) Thời gian vòi thứ hai chảy một mình để đầy bể là: x+2 (giờ).
b) Phần bể vòi thứ nhất chảy được trong 1 giờ là: \frac{1}{x} (bể/giờ).
Phần bể vòi thứ hai chảy được trong 1 giờ là: \frac{1}{x+2} (bể/giờ).
c) Phần bể cả hai vòi chảy được trong 1 giờ là tổng phần bể mà mỗi vòi chảy được trong 1 giờ:
\frac{1}{x} + \frac{1}{x+2}
Quy đồng mẫu thức: x(x+2).
= \frac{1(x+2) + 1x}{x(x+2)}
= \frac{x+2+x}{x(x+2)}
= \frac{2x+2}{x(x+2)}
Giải bài 7 (Trang 43)
Đề bài:
Chi đoàn thanh niên dự định trồng 120 cây xanh. Gọi $x$ là số đoàn viên ban đầu. Khi thực hiện, được tăng cường thêm 3 đoàn viên. Viết phân thức biểu thị theo $x$:
a) Số cây mỗi đoàn viên trồng theo dự định;
b) Số cây mỗi đoàn viên trồng theo thực tế;
c) Số cây mỗi đoàn viên trồng theo dự định nhiều hơn số cây mỗi đoàn viên trồng theo thực tế.
Phương pháp giải:
Số cây mỗi đoàn viên trồng bằng tổng số cây chia cho số đoàn viên.
Đáp án:
a) Số cây mỗi đoàn viên trồng theo dự định là: \frac{120}{x} (cây/đoàn viên).
b) Số đoàn viên thực tế là x+3.
Số cây mỗi đoàn viên trồng theo thực tế là: \frac{120}{x+3} (cây/đoàn viên).
c) Số cây mỗi đoàn viên trồng theo dự định nhiều hơn thực tế là:
\frac{120}{x} - \frac{120}{x+3}
Quy đồng mẫu thức: x(x+3).
= \frac{120(x+3) - 120x}{x(x+3)}
= \frac{120x + 360 - 120x}{x(x+3)}
= \frac{360}{x(x+3)}
Giải bài 8 (Trang 43)
Đề bài:
Ba con lợn ăn cùng một loại thức ăn. Biểu đồ cho biết số ngày mỗi con lợn ăn hết một bao thức ăn. Hỏi cả ba con lợn ăn trong $x$ ngày thì cần bao nhiêu bao thức ăn?
Phân tích yêu cầu và dữ liệu từ biểu đồ:
Biểu đồ cho thấy:
- Con lợn thứ nhất ăn hết 1 bao trong 3 ngày.
- Con lợn thứ hai ăn hết 1 bao trong 6 ngày.
- Con lợn thứ ba ăn hết 1 bao trong 4 ngày.
Ta cần tính lượng thức ăn cả ba con tiêu thụ trong 1 ngày, sau đó nhân với $x$ để ra tổng số bao thức ăn cho $x$ ngày.
Phương pháp giải:
- Xác định lượng thức ăn mỗi con lợn tiêu thụ trong 1 ngày.
- Tính tổng lượng thức ăn cả ba con lợn tiêu thụ trong 1 ngày.
- Tính tổng lượng thức ăn cả ba con lợn tiêu thụ trong $x$ ngày.
Đáp án:
Lượng thức ăn con lợn thứ nhất ăn trong 1 ngày: \frac{1}{3} (bao/ngày).
Lượng thức ăn con lợn thứ hai ăn trong 1 ngày: \frac{1}{6} (bao/ngày).
Lượng thức ăn con lợn thứ ba ăn trong 1 ngày: \frac{1}{4} (bao/ngày).Tổng lượng thức ăn cả ba con lợn ăn trong 1 ngày là:
\frac{1}{3} + \frac{1}{6} + \frac{1}{4}
Quy đồng mẫu thức chung là 12:
= \frac{4}{12} + \frac{2}{12} + \frac{3}{12}
= \frac{4+2+3}{12} = \frac{9}{12} = \frac{3}{4} (bao/ngày).Lượng thức ăn cả ba con lợn ăn trong $x$ ngày là:
x \times \frac{3}{4} = \frac{3x}{4} (bao).
Đáp Án/Kết Quả
Các bài tập từ trang 42 đến 43 sách Toán lớp 8 Cánh Diều tập 1 xoay quanh việc thực hiện phép cộng, trừ phân thức đại số và áp dụng vào giải các bài toán thực tế.
- Các bài 1, 2, 3 yêu cầu thực hiện trực tiếp các phép cộng, trừ phân thức, đôi khi cần quy đồng mẫu thức.
- Bài 4 yêu cầu rút gọn biểu thức phân thức và tính giá trị của biểu thức đó.
- Các bài 5, 6, 7, 8 là những bài toán có lời văn, đòi hỏi học sinh lập các biểu thức phân thức từ dữ kiện đề bài, sau đó thực hiện các phép toán hoặc phân tích kết quả.
Việc nắm vững quy tắc cộng, trừ phân thức và kỹ năng rút gọn phân thức là chìa khóa để giải quyết thành công các bài toán này.
Kết Luận
Qua bài viết giải toán lớp 8 trang 40 sách Cánh Diều tập 1, chúng ta đã cùng nhau ôn tập và thực hành các dạng bài tập về phép cộng, phép trừ phân thức đại số. Việc thành thạo kỹ năng này không chỉ giúp các em làm tốt các bài kiểm tra mà còn là nền tảng quan trọng cho các chương trình học tiếp theo. Hãy luyện tập thường xuyên để ghi nhớ và vận dụng linh hoạt các kiến thức đã học.
Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.

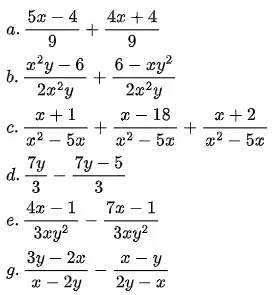 Hình ảnh bài 1 trang 42
Hình ảnh bài 1 trang 42 Hình ảnh bài 2 trang 42
Hình ảnh bài 2 trang 42 Hình ảnh bài 3 trang 42
Hình ảnh bài 3 trang 42 Hình ảnh bài 8 trang 43
Hình ảnh bài 8 trang 43











