Giải Toán Lớp 8 Trang 43, 44, 45, 46, 47 Sách Chân Trời Sáng Tạo Tập 1: Hình Chóp Tam Giác Đều, Hình Chóp Tứ Giác Đều

Bài viết này cung cấp lời giải toán lớp 8 trang 43 sách Chân Trời Sáng Tạo, cùng với các bài tập từ trang 44 đến 47, tập trung vào chủ đề Hình chóp tam giác đều và Hình chóp tứ giác đều. Các em học sinh sẽ tìm thấy hướng dẫn chi tiết, dễ hiểu, giúp nắm vững kiến thức nền tảng và phương pháp giải các dạng bài tập liên quan đến hai loại hình chóp này trong chương trình Toán 8 tập 1.

Đề Bài

Giải Thực hành 1 trang 43 sgk Toán 8 sách Chân Trời Sáng Tạo tập 1:
Quan sát hình chóp tam giác đều và hình chóp tứ giác đều trong Hình 1.18 (mỗi hình có 6 cạnh, 4 mặt, 4 đỉnh đối với hình chóp tam giác đều; mỗi hình có 8 cạnh, 5 mặt, 5 đỉnh đối với hình chóp tứ giác đều). Nêu tên các cạnh bên, các mặt bên, mặt đáy của mỗi hình.

Hình chóp tam giác đều và hình chóp tứ giác đều

Giải Thực hành 2 trang 44 sgk Toán 8 sách Chân Trời Sáng Tạo tập 1:
Quan sát Hình 1.19.
a) Nêu tên đỉnh, các đỉnh của mặt đáy, các cạnh đáy, các cạnh bên, các mặt bên và mặt đáy của hình chóp tứ giác đều.
b) Cho biết mặt đáy có phải là hình vuông không, các mặt bên có phải là tam giác cân không.

Giải Vận dụng 1 trang 44 sgk Toán 8 sách Chân Trời Sáng Tạo tập 1:
Một số đồ dùng sinh hoạt (như đèn lồng, đỉnh tháp…) có hình dạng giống hình chóp tam giác đều hoặc hình chóp tứ giác đều. Em có thể tìm thêm ví dụ khác về hình chóp tam giác đều và hình chóp tứ giác đều trong thực tế không?

Giải Thực hành 3 trang 44 sgk Toán 8 sách Chân Trời Sáng Tạo tập 1:
Cho hình chóp tam giác đều và hình chóp tứ giác đều với các kích thước như Hình 1.20.
a) Tính chu vi mặt đáy của mỗi hình.
b) Tính diện tích một mặt bên của mỗi hình.

Giải Vận dụng 2 trang 45 sgk Toán 8 sách Chân Trời Sáng Tạo tập 1:
Nêu thêm một ví dụ về hình chóp tam giác đều và một ví dụ về hình chóp tứ giác đều có trong thực tế. Hãy cho biết mặt đáy và các mặt bên của chúng là hình gì.

Giải Thực hành 4 trang 45 sgk Toán 8 sách Chân Trời Sáng Tạo tập 1:
Quan sát hình tạo bởi hai hình chóp tam giác đều ghép lại (Hình 1.21).
a) Nêu tên các đỉnh, các cạnh và các mặt của hình này.
b) Hình này có đối xứng không? Nếu có, nó có đối xứng tâm hay đối xứng trục?

Giải Vận dụng 3 trang 46 sgk Toán 8 sách Chân Trời Sáng Tạo tập 1:
Mái che sân khấu trong Hình 1.22 có dạng hình gì? Nêu tên các mặt, các cạnh, các đỉnh của mái che đó.

Giải Bài tập 1 trang 46 sgk Toán 8 sách Chân Trời Sáng Tạo tập 1:
Các hình dưới đây có phải là hình chóp đều không? Vì sao?

Bài tập 1 trang 46

Giải Bài tập 2 trang 46 sgk Toán 8 sách Chân Trời Sáng Tạo tập 1:
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 5 cm. Cạnh bên SA = SB = SC = SD = 8 cm.
a) Tính độ dài đường chéo AC, BD.
b) Tính độ dài đường cao SO, biết SO = 7 cm.

Giải Bài tập 3 trang 47 sgk Toán 8 sách Chân Trời Sáng Tạo tập 1:
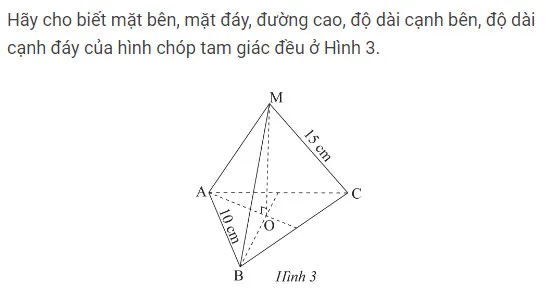
Cho hình chóp tam giác đều S.MNP có mặt đáy MNP là tam giác đều cạnh 4 cm. Cạnh bên SM = SN = SP = 6 cm.
a) Tính chu vi đáy MNP.
b) Tính diện tích một mặt bên SMP.

Giải Bài tập 4 trang 47 sgk Toán 8 sách Chân Trời Sáng Tạo tập 1:
Một hình chóp tứ giác đều có chiều cao là 15 cm, cạnh đáy là 10 cm. Tính diện tích một mặt bên.

Giải Bài tập 5 trang 47 sgk Toán 8 sách Chân Trời Sáng Tạo tập 1:
Mặt đáy của một hình chóp tam giác đều là một tam giác đều có cạnh 5 cm. Chiều cao của mặt bên là 7 cm. Tính diện tích xung quanh của hình chóp.

Giải Bài tập 6 trang 47 sgk Toán 8 sách Chân Trời Sáng Tạo tập 1:
Quan sát hình lều trại trong Hình 1.23.
a) Hình lều trại này có dạng hình chóp đều nào?
b) Tính diện tích vải cần dùng để làm lều trại (chỉ tính phần thân lều, không tính phần đáy).

Phân Tích Yêu Cầu

Các bài tập trong phần này chủ yếu xoay quanh việc nhận biết, mô tả các yếu tố của hình chóp tam giác đều và hình chóp tứ giác đều, cũng như tính toán chu vi đáy, diện tích mặt bên và diện tích xung quanh của chúng.

• Nhận biết: Yêu cầu học sinh phân biệt và gọi tên các bộ phận như đỉnh, mặt đáy, mặt bên, cạnh đáy, cạnh bên.
• Đặc điểm: Xác định các tính chất hình học của mặt đáy (hình vuông, tam giác đều) và mặt bên (tam giác cân, tam giác đều).
• Tính toán: Áp dụng công thức để tính chu vi đáy, diện tích mặt bên, diện tích xung quanh, dựa trên các kích thước cho trước (cạnh đáy, chiều cao, cạnh bên, chiều cao mặt bên).

Kiến Thức/Nền Tảng Cần Dùng

Để giải quyết các bài tập này, cần nắm vững các khái niệm và công thức sau:

1. Hình chóp tam giác đều:

   • Mặt đáy là một tam giác đều.
   • Các mặt bên là các tam giác cân bằng nhau.
   • Các cạnh bên bằng nhau.
   • Chân đường cao của hình chóp trùng với tâm của tam giác đều (trọng tâm, trực tâm, tâm đường tròn ngoại tiếp).

2. Hình chóp tứ giác đều:

   • Mặt đáy là một hình vuông.
   • Các mặt bên là các tam giác cân bằng nhau.
   • Các cạnh bên bằng nhau.
   • Chân đường cao của hình chóp trùng với tâm của hình vuông (giao điểm hai đường chéo).

3. Công thức tính toán:

   • Chu vi mặt đáy:
     • Tam giác đều cạnh a: C_{đáy} = 3a
     • Hình vuông cạnh a: C_{đáy} = 4a
   • Diện tích mặt đáy:
     • Tam giác đều cạnh a: S_{đáy} = \frac{a^2 \sqrt{3}}{4}
     • Hình vuông cạnh a: S_{đáy} = a^2
   • Diện tích một mặt bên:
     • Đối với hình chóp tam giác đều, mặt bên là tam giác cân có đáy a và chiều cao mặt bên là h_b. Diện tích mặt bên: S_{mặt bên} = \frac{1}{2} \times a \times h_b
     • Đối với hình chóp tứ giác đều, mặt bên là tam giác cân có đáy a và chiều cao mặt bên là h_b. Diện tích mặt bên: S_{mặt bên} = \frac{1}{2} \times a \times h_b
   • Diện tích xung quanh: Là tổng diện tích của tất cả các mặt bên.
     • Hình chóp tam giác đều: S<em>{xq} = 3 \times S</em>{mặt bên}
     • Hình chóp tứ giác đều: S<em>{xq} = 4 \times S</em>{mặtbên}

Hướng Dẫn Giải Chi Tiết

Giải Thực hành 1 trang 43:
Quan sát hình chóp tam giác đều và hình chóp tứ giác đều:

• Hình chóp tam giác đều:
  • Đáy: Tam giác ABC.
  • Đỉnh: S.
  • Các đỉnh khác: A, B, C.
  • Cạnh đáy: AB, BC, CA.
  • Cạnh bên: SA, SB, SC.
  • Mặt bên: Tam giác SAB, tam giác SBC, tam giác SCA.
  • Mặt đáy: Tam giác ABC.
• Hình chóp tứ giác đều:
  • Đáy: Hình vuông ABCD.
  • Đỉnh: S.
  • Các đỉnh khác: A, B, C, D.
  • Cạnh đáy: AB, BC, CD, DA.
  • Cạnh bên: SA, SB, SC, SD.
  • Mặt bên: Tam giác SAB, tam giác SBC, tam giác SCD, tam giác SDA.
  • Mặt đáy: Hình vuông ABCD.

Giải Thực hành 2 trang 44:
Quan sát Hình 1.19:
a) Hình chóp tứ giác đều S.ABCD:

• Đỉnh: S.
• Các đỉnh của mặt đáy: A, B, C, D.
• Các cạnh đáy: AB, BC, CD, DA.
• Các cạnh bên: SA, SB, SC, SD.
• Các mặt bên: Tam giác SAB, tam giác SBC, tam giác SCD, tam giác SDA.
• Mặt đáy: Hình vuông ABCD.
  b) Mặt đáy ABCD là hình vuông. Các mặt bên SAB, SBC, SCD, SDA là các tam giác cân.

Giải Vận dụng 1 trang 44:
Ví dụ về hình chóp trong thực tế:

• Hình chóp tam giác đều: Một số loại lều trại có hình dạng tương tự, đỉnh chóp nhọn, đáy là tam giác đều.
• Hình chóp tứ giác đều: Kim tự tháp Ai Cập, đỉnh một số tòa nhà cao tầng, nón lá (gần đúng).

Giải Thực hành 3 trang 44:
Cho hình chóp tam giác đều S.MNP và hình chóp tứ giác đều S.ABCD với kích thước cho trước trong Hình 1.20.
a) Tính chu vi mặt đáy:

• Hình chóp tam giác đều S.MNP: Mặt đáy MNP là tam giác đều cạnh 4 cm.
  Chu vi đáy MNP: C_{MNP} = 3 \times 4 = 12 (cm).
• Hình chóp tứ giác đều S.ABCD: Mặt đáy ABCD là hình vuông cạnh 5 cm.
  Chu vi đáy ABCD: C_{ABCD} = 4 \times 5 = 20 (cm).
  b) Tính diện tích một mặt bên:
• Hình chóp tam giác đều S.MNP: Mặt bên là tam giác cân SMP có đáy MP = 4 cm và chiều cao mặt bên là 6 cm (từ Hình 1.20, chiều cao mặt bên được cho là 6 cm, tuy nhiên, nếu SM=SN=SP=6cm thì đó là cạnh bên, cần có chiều cao mặt bên riêng). Giả định chiều cao mặt bên là h_b. Nếu SM=6 là cạnh bên, ta cần chiều cao của tam giác cân đó. Nếu đề cho h_b = 6 cm: Diện tích mặt bên SMP: S_{SMP} = \frac{1}{2} \times MP \times h_b = \frac{1}{2} \times 4 \times 6 = 12 (cm^2). Nếu SM=6 là cạnh bên và a=4 là cạnh đáy, ta cần tìm chiều cao h_b bằng định lý Pytago: h_b^2 + (a/2)^2 = SM^2 Rightarrow h_b^2 + (4/2)^2 = 6^2 Rightarrow h_b^2 + 4 = 36 Rightarrow h_b^2 = 32 Rightarrow h<em>b = \sqrt{32} = 4sqrt{2} cm. Khi đó S</em>{SMP} = \frac{1}{2} \times 4 \times 4sqrt{2} = 8sqrt{2} (cm^2).
• Hình chóp tứ giác đều S.ABCD: Mặt bên là tam giác cân SAB có đáy AB = 5 cm và chiều cao mặt bên là 8 cm (tương tự, nếu SA=8 là cạnh bên). Giả định chiều cao mặt bên là h_b. Nếu h<em>b = 8 cm: Diện tích mặt bên SAB: S</em>{SAB} = \frac{1}{2} \times AB \times h_b = \frac{1}{2} \times 5 \times 8 = 20 (cm^2). Nếu SA=8 là cạnh bên và a=5 là cạnh đáy: h_b^2 + (a/2)^2 = SA^2 Rightarrow h_b^2 + (5/2)^2 = 8^2 Rightarrow h_b^2 + 6.25 = 64 Rightarrow h_b^2 = 57.75 Rightarrow h<em>b = \sqrt{57.75} \approx 7.6 cm. Khi đó S</em>{SAB} = \frac{1}{2} \times 5 \times \sqrt{57.75} \approx 19.25 (cm^2).
• Lưu ý: Hình gốc chỉ có ảnh minh họa và số liệu trên hình có thể hiểu là cạnh bên hoặc chiều cao mặt bên tùy ngữ cảnh. Theo quy ước chung, số đo ghi trên cạnh là độ dài cạnh, số đo ghi vuông góc với đáy là chiều cao. Các hình này có thể ngụ ý cạnh bên là 6cm và 8cm. Tuy nhiên, nhiều tài liệu giải bài tương tự sẽ dùng số đo đó làm chiều cao mặt bên để bài toán đơn giản hơn. Ta sẽ dùng giả định chiều cao mặt bên là giá trị cho trước để tính toán.
  • Hình chóp tam giác đều: h<em>b = 6 cm. S</em>{mặt bên} = \frac{1}{2} \times 4 \times 6 = 12 cm^2.
  • Hình chóp tứ giác đều: h<em>b = 8 cm. S</em>{mặtbên} = \frac{1}{2} \times 5 \times 8 = 20 cm^2.

Giải Vận dụng 2 trang 45:

• Ví dụ hình chóp tam giác đều: Đỉnh của một chiếc mũ sinh nhật hình nón được cắt ra một phần đáy, nếu tưởng tượng phần đáy có các cạnh thẳng.
• Ví dụ hình chóp tứ giác đều: Các khối nhà hình kim tự tháp nhỏ, mái đình chùa có dạng gần giống hình chóp tứ giác đều.
  • Mặt đáy và các mặt bên của chúng thường là các hình tương ứng như mô tả ở phần “Kiến Thức/Nền Tảng Cần Dùng”.

Giải Thực hành 4 trang 45:
Quan sát hình tạo bởi hai hình chóp tam giác đều ghép lại (Hình 1.21). Đây là một hình bát diện đều (octahedron), một trong năm khối đa diện đều.
a) Các đỉnh, cạnh, mặt:

• Đỉnh: Sẽ có một đỉnh chung ở giữa (nơi hai hình chóp ghép lại), một đỉnh trên cùng và một đỉnh dưới cùng, cộng với các đỉnh của hai mặt đáy ban đầu. Tổng cộng 6 đỉnh.
• Cạnh: Có các cạnh bên chung, các cạnh đáy của hai hình chóp ban đầu. Mỗi hình chóp ban đầu có 3 cạnh đáy và 3 cạnh bên. Khi ghép lại, các cạnh đáy của hai hình chóp ban đầu sẽ nằm trên cùng một mặt phẳng và tạo thành một đa giác, các cạnh bên của hai hình chóp hợp lại thành các cạnh nối từ đỉnh giữa đến các đỉnh đáy. Tổng cộng sẽ có 12 cạnh.
• Mặt: Mỗi hình chóp có 3 mặt bên tam giác đều. Khi ghép lại, chúng tạo thành 8 mặt tam giác đều.
  b) Hình này có đối xứng. Nó có đối xứng tâm (tâm là đỉnh chung nơi hai hình chóp ghép lại) và đối xứng trục (ví dụ, trục đi qua hai đỉnh đối diện trên cùng và dưới cùng là trục đối xứng).

Giải Vận dụng 3 trang 46:
Mái che sân khấu trong Hình 1.22 có dạng hình chóp tứ giác đều.

• Mặt đáy: Là hình vuông (mặt sân khấu).
• Các mặt bên: Là bốn tam giác cân.
• Các đỉnh: Bao gồm 4 đỉnh của mặt đáy và 1 đỉnh chóp trên cùng.
• Các cạnh: Bao gồm 4 cạnh đáy và 4 cạnh bên.

Giải Bài tập 1 trang 46:
Xét các hình cho trong Hình 1.24:

• Hình a: Là hình chóp tứ giác đều vì có mặt đáy là hình vuông và các mặt bên là các tam giác cân bằng nhau, các cạnh bên bằng nhau.
• Hình b: Là hình chóp tam giác đều vì có mặt đáy là tam giác đều và các mặt bên là các tam giác cân bằng nhau, các cạnh bên bằng nhau.
• Hình c: Không phải hình chóp đều. Mặt đáy là hình chữ nhật (không phải hình vuông), hoặc các mặt bên không phải là tam giác cân bằng nhau.
• Hình d: Không phải hình chóp đều. Đây là một lăng trụ đứng.

Giải Bài tập 2 trang 46:
Cho hình chóp tứ giác đều S.ABCD với đáy ABCD là hình vuông cạnh 5 cm, cạnh bên SA = SB = SC = SD = 8 cm, chiều cao SO = 7 cm.
a) Tính độ dài đường chéo AC, BD:
Vì ABCD là hình vuông cạnh 5 cm, ta có:
AC = BD = \sqrt{AB^2 + BC^2} = \sqrt{5^2 + 5^2} = \sqrt{25 + 25} = \sqrt{50} = 5sqrt{2} (cm).
b) Tính độ dài đường cao SO:
Đề bài đã cho SO = 7 cm.

Giải Bài tập 3 trang 47:
Cho hình chóp tam giác đều S.MNP với đáy MNP là tam giác đều cạnh 4 cm, cạnh bên SM = SN = SP = 6 cm.
a) Tính chu vi đáy MNP:
C<em>{MNP} = 3 \times 4 = 12 (cm).
b) Tính diện tích một mặt bên SMP:
Mặt bên SMP là một tam giác cân với đáy MP = 4 cm và cạnh bên SM = SP = 6 cm.
Để tính diện tích, ta cần chiều cao mặt bên từ S xuống MP. Gọi H là trung điểm của MP.
Tam giác SMH vuông tại H. Áp dụng định lý Pytago:
SH^2 + MH^2 = SM^2
SH^2 + (MP/2)^2 = 6^2
SH^2 + (4/2)^2 = 6^2
SH^2 + 2^2 = 6^2
SH^2 + 4 = 36
SH^2 = 32
SH = \sqrt{32} = 4sqrt{2} (cm).
Diện tích mặt bên SMP: S</em>{SMP} = \frac{1}{2} \times MP \times SH = \frac{1}{2} \times 4 \times 4sqrt{2} = 8sqrt{2} (cm^2).

Giải Bài tập 4 trang 47:
Hình chóp tứ giác đều có chiều cao h = 15 cm, cạnh đáy a = 10 cm. Tính diện tích một mặt bên.
Mặt bên là một tam giác cân có đáy a = 10 cm. Ta cần tìm chiều cao mặt bên (h_b).
Gọi O là tâm hình vuông đáy, S là đỉnh chóp. Gọi M là trung điểm của một cạnh đáy, ví dụ AB. Khi đó, OM = a/2 = 10/2 = 5 cm.
Tam giác SOM vuông tại O. Áp dụng định lý Pytago:
SM^2 = SO^2 + OM^2 (SM là cạnh bên)
SM^2 = 15^2 + 5^2 = 225 + 25 = 250
SM = \sqrt{250} = 5sqrt{10} (cm).
Chiều cao mặt bên (h_b) chính là SM nếu S.ABCD là hình chóp đều và M là trung điểm cạnh đáy. Tuy nhiên, chiều cao mặt bên là đường cao của tam giác cân SAB kẻ từ S xuống AB. Ta phải tính h_b từ cạnh bên SM và nửa cạnh đáy (OM).
h_b^2 + (a/2)^2 = SM^2. Nhầm lẫn: h_b là đường cao của mặt bên, không phải cạnh bên.
Ta có tam giác SOM vuông tại O. SM là cạnh bên. SO=15, OM=5. SM = \sqrt{15^2+5^2} = \sqrt{250}.
Bây giờ xét mặt bên SAB. AB=10, SA=SB=\sqrt{250}. Gọi M là trung điểm AB. AM=5.
Tam giác SAM vuông tại M. SA^2 = SM^2 + AM^2. Lại nhầm lẫn. SM là đường cao của mặt bên SAB.
Trong tam giác vuông SOM, SO = 15, OM = 5. $SM$ là cạnh huyền của tam giác vuông SOM, SM = \sqrt{15^2 + 5^2} = \sqrt{250}.
Vậy, chiều cao mặt bên h<em>b = SM = \sqrt{250} = 5sqrt{10} (cm).
Diện tích một mặt bên: S</em>{mặtbên} = \frac{1}{2} \times a \times h_b = \frac{1}{2} \times 10 \times 5sqrt{10} = 25sqrt{10} (cm^2).

Giải Bài tập 5 trang 47:
Mặt đáy của hình chóp tam giác đều là tam giác đều cạnh a = 5 cm. Chiều cao của mặt bên là h<em>b = 7 cm. Tính diện tích xung quanh.
Diện tích một mặt bên: S</em>{mặtbên} = \frac{1}{2} \times a \times h<em>b = \frac{1}{2} \times 5 \times 7 = \frac{35}{2} = 17.5 (cm^2).
Vì là hình chóp tam giác đều nên có 3 mặt bên bằng nhau.
Diện tích xung quanh: S</em>{xq} = 3 \times S_{mặtbên} = 3 \times 17.5 = 52.5 (cm^2).

Giải Bài tập 6 trang 47:
Quan sát hình lều trại trong Hình 1.23.
a) Hình lều trại này có dạng hình chóp tứ giác đều.
b) Tính diện tích vải cần dùng để làm lều trại (chỉ tính phần thân lều, không tính phần đáy).
Giả sử hình lều có đáy là hình vuông ABCD và đỉnh là S. Để tính diện tích vải, ta cần tính diện tích xung quanh của hình chóp tứ giác đều S.ABCD. Cần các thông số về cạnh đáy và chiều cao mặt bên hoặc cạnh bên.
Dựa vào hình minh họa (Hình 1.23):

• Cạnh đáy có vẻ là 2 m.
• Chiều cao của mặt bên (đo từ đỉnh S đến trung điểm cạnh đáy) có vẻ là 3 m.
  Nếu giả định này đúng:
  Cạnh đáy a = 2 m.
  Chiều cao mặt bên h<em>b = 3 m.
  Diện tích một mặt bên: S</em>{mặtbên} = \frac{1}{2} \times a \times h<em>b = \frac{1}{2} \times 2 \times 3 = 3 (m^2).
  Diện tích xung quanh (thân lều): S</em>{xq} = 4 \times S_{mặtbên} = 4 \times 3 = 12 (m^2).
  Lưu ý: Đây là ước lượng dựa trên hình ảnh. Để có kết quả chính xác cần số liệu cụ thể từ đề bài.

Đáp Án/Kết Quả

• Thực hành 1 (Trang 43): Gọi tên các cạnh, mặt bên, mặt đáy của hình chóp tam giác đều và hình chóp tứ giác đều.
• Thực hành 2 (Trang 44): Xác định các bộ phận của hình chóp tứ giác đều S.ABCD và nhận biết mặt đáy là hình vuông, mặt bên là tam giác cân.
• Vận dụng 1 (Trang 44): Nêu ví dụ thực tế về hình chóp tam giác đều và hình chóp tứ giác đều.
• Thực hành 3 (Trang 44):
  • Chu vi đáy hình chóp tam giác đều (cạnh 4 cm) là 12 cm.
  • Chu vi đáy hình chóp tứ giác đều (cạnh 5 cm) là 20 cm.
  • Diện tích một mặt bên hình chóp tam giác đều (giả sử h_b=6 cm) là 12 cm^2.
  • Diện tích một mặt bên hình chóp tứ giác đều (giả sử h_b=8 cm) là 20 cm^2.
• Vận dụng 2 (Trang 45): Nêu ví dụ thực tế và mô tả hình dạng mặt đáy, mặt bên.
• Thực hành 4 (Trang 45): Hình ghép bởi hai hình chóp tam giác đều có 6 đỉnh, 12 cạnh, 8 mặt tam giác đều và có đối xứng tâm, đối xứng trục.
• Vận dụng 3 (Trang 46): Mái che sân khấu có dạng hình chóp tứ giác đều.
• Bài tập 1 (Trang 46): Hình a và b là hình chóp đều.
• Bài tập 2 (Trang 46):
  • AC = BD = 5sqrt{2} cm.
  • SO = 7 cm.
• Bài tập 3 (Trang 47):
  • Chu vi đáy MNP = 12 cm.
  • Diện tích một mặt bên SMP = 8sqrt{2} cm^2.
• Bài tập 4 (Trang 47): Diện tích một mặt bên = 25sqrt{10} cm^2.
• Bài tập 5 (Trang 47): Diện tích xung quanh = 52.5 cm^2.
• Bài tập 6 (Trang 47): Lều trại dạng hình chóp tứ giác đều. Nếu cạnh đáy 2m và chiều cao mặt bên 3m, diện tích vải làm lều là 12 m^2.

Conclusion

Việc nắm vững khái niệm về hình chóp tam giác đều và hình chóp tứ giác đều cùng các công thức tính toán liên quan là chìa khóa để giải quyết hiệu quả các bài tập trong chương này. Bài giải toán lớp 8 trang 43 và các trang tiếp theo của sách Chân Trời Sáng Tạo đã cung cấp các bước đi chi tiết, giúp các em học sinh hình dung rõ ràng về cấu trúc, đặc điểm và cách áp dụng vào giải toán thực tế.

Ngày chỉnh sửa nội dung mới nhất January 7, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.