Giải Toán 9 Bài 1 trang 73 Tập 2 Cánh Diều: Đường Tròn Ngoại Tiếp, Nội Tiếp Tam Giác

by Thầy Đông · January 8, 2026

Rate this post

Trong chương trình Toán lớp 9, việc hiểu rõ khái niệm đường tròn ngoại tiếp và đường tròn nội tiếp tam giác là vô cùng quan trọng. Bài viết này sẽ cung cấp lời giải chi tiết và phân tích cho giải toán 9 tập 2 bài 1 theo sách Cánh Diều, giúp học sinh nắm vững kiến thức nền tảng này. Chúng ta sẽ cùng nhau xem xét các hình vẽ để phân biệt đâu là đường tròn ngoại tiếp và đâu là đường tròn nội tiếp tam giác ABC, đồng thời giải thích lý do vì sao.

Đề Bài

Trong các hình 15a, 15b, 15c, 15d, ở hình nào ta có đường tròn (O) là đường tròn ngoại tiếp tam giác ABC? Ở hình nào ta có đường tròn (O) là đường tròn nội tiếp tam giác ABC? Vì sao?

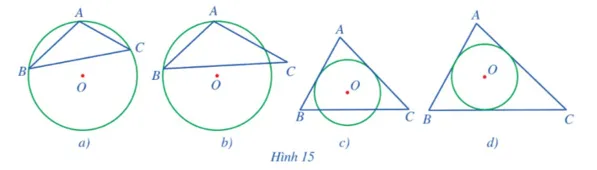Minh họa các hình vẽ trong Bài 1 trang 73 Toán 9 Tập 2 Cánh diều

Phân Tích Yêu Cầu

Đề bài yêu cầu chúng ta xác định vai trò của đường tròn (O) đối với tam giác ABC trong từng hình cụ thể (a, b, c, d). Cụ thể, chúng ta cần nhận diện:

Đường tròn (O) là đường tròn ngoại tiếp tam giác ABC.
Đường tròn (O) là đường tròn nội tiếp tam giác ABC.

Để trả lời câu hỏi này, chúng ta cần dựa vào định nghĩa và tính chất của đường tròn ngoại tiếp và đường tròn nội tiếp tam giác.

Kiến Thức/Nền Tảng Cần Dùng

Trước khi đi vào giải chi tiết từng hình, chúng ta cần nắm vững các định nghĩa sau:

Đường tròn ngoại tiếp tam giác: Là đường tròn đi qua cả ba đỉnh của tam giác đó. Tâm của đường tròn ngoại tiếp là tâm đường tròn ngoại tiếp, giao điểm của ba đường trung trực của tam giác.
Đường tròn nội tiếp tam giác: Là đường tròn tiếp xúc với cả ba cạnh của tam giác đó. Tâm của đường tròn nội tiếp là tâm đường tròn nội tiếp, giao điểm của ba đường phân giác của tam giác.

Dựa vào hai định nghĩa này, chúng ta sẽ xem xét từng hình vẽ để đưa ra kết luận chính xác.

Hướng Dẫn Giải Chi Tiết

Chúng ta sẽ lần lượt xem xét từng hình:

1. Phân tích Hình 15a

Quan sát Hình 15a, ta thấy đường tròn tâm (O) có ba điểm A, B, C cùng nằm trên đường tròn.
Theo định nghĩa, đường tròn đi qua cả ba đỉnh của tam giác được gọi là đường tròn ngoại tiếp tam giác.
Do đó, ở Hình 15a, đường tròn (O) là đường tròn ngoại tiếp tam giác ABC.

2. Phân tích Hình 15b

Trong Hình 15b, đường tròn tâm (O) đi qua hai đỉnh A và B của tam giác ABC. Tuy nhiên, đỉnh C không nằm trên đường tròn này.
Vì đường tròn (O) không đi qua tất cả ba đỉnh A, B, C, nên nó không thỏa mãn định nghĩa đường tròn ngoại tiếp tam giác ABC.
Đồng thời, đường tròn này cũng không tiếp xúc với cả ba cạnh BC, CA, AB.
Do đó, ở Hình 15b, đường tròn (O) không là đường tròn ngoại tiếp tam giác ABC và cũng không là đường tròn nội tiếp tam giác ABC.

3. Phân tích Hình 15c

Quan sát Hình 15c, đường tròn tâm (O) có ba đỉnh A, B, C nằm trên đường tròn. Điều này cho thấy đường tròn này là đường tròn ngoại tiếp tam giác ABC.
Tuy nhiên, chúng ta cần kiểm tra xem nó có phải là đường tròn nội tiếp hay không.
Đường tròn nội tiếp phải tiếp xúc với cả ba cạnh của tam giác. Trong Hình 15c, đường tròn (O) đi qua ba đỉnh nhưng không tiếp xúc với các cạnh AB, BC, CA. Ví dụ, nó rõ ràng không tiếp xúc với cạnh BC.
Do đó, ở Hình 15c, đường tròn (O) là đường tròn ngoại tiếp tam giác ABC nhưng không là đường tròn nội tiếp tam giác ABC.

4. Phân tích Hình 15d

Trong Hình 15d, ta thấy đường tròn tâm (O) tiếp xúc với cả ba cạnh AB, BC và CA của tam giác ABC.
Theo định nghĩa, đường tròn tiếp xúc với cả ba cạnh của tam giác được gọi là đường tròn nội tiếp tam giác.
Các điểm tiếp xúc của đường tròn với các cạnh là các điểm nằm trên cả đường tròn và trên cạnh tương ứng.
Do đó, ở Hình 15d, đường tròn (O) là đường tròn nội tiếp tam giác ABC.

Mẹo kiểm tra

Để xác định đường tròn ngoại tiếp, hãy kiểm tra xem đường tròn có “bao quanh” tam giác và đi qua chính xác ba đỉnh của nó hay không.
Để xác định đường tròn nội tiếp, hãy kiểm tra xem đường tròn có “nằm gọn bên trong” tam giác và “chạm” vào cả ba cạnh của nó hay không.

Lỗi hay gặp

Nhầm lẫn giữa đường tròn ngoại tiếp và nội tiếp: Học sinh có thể nhầm lẫn định nghĩa, ví dụ cho rằng đường tròn nội tiếp là đường tròn đi qua ba đỉnh.
Sai sót khi quan sát hình vẽ: Có thể nhìn nhầm xem đường tròn có đi qua đỉnh hay tiếp xúc với cạnh hay không.

Đáp Án/Kết Quả

Dựa trên phân tích chi tiết ở trên, kết quả cho từng hình như sau:

Hình 15a: Đường tròn (O) là đường tròn ngoại tiếp tam giác ABC.
Hình 15b: Đường tròn (O) không là đường tròn ngoại tiếp và không là đường tròn nội tiếp tam giác ABC.
Hình 15c: Đường tròn (O) là đường tròn ngoại tiếp tam giác ABC.
Hình 15d: Đường tròn (O) là đường tròn nội tiếp tam giác ABC.

Kết Luận

Qua bài tập giải toán 9 tập 2 bài 1, chúng ta đã củng cố vững chắc kiến thức về hai loại đường tròn quan trọng liên quan đến tam giác: đường tròn ngoại tiếp và đường tròn nội tiếp. Việc phân biệt rõ ràng dựa trên định nghĩa đường tròn đi qua ba đỉnh (ngoại tiếp) và đường tròn tiếp xúc ba cạnh (nội tiếp) sẽ giúp các em tự tin giải quyết các bài toán hình học phức tạp hơn trong tương lai.

Ngày chỉnh sửa nội dung mới nhất January 8, 2026 by Thầy Đông

Thầy Đông

Thầy Đông – Giảng viên Đại học Công nghiệp Hà Nội, giáo viên luyện thi THPT
Thầy Đông bắt đầu sự nghiệp tại một trường THPT ở quê nhà, sau đó trúng tuyển giảng viên Đại học Công nghiệp Hà Nội nhờ chuyên môn vững và kinh nghiệm giảng dạy thực tế. Với nhiều năm đồng hành cùng học sinh, thầy được biết đến bởi phong cách giảng dạy rõ ràng, dễ hiểu và gần gũi. Hiện thầy giảng dạy tại dehocsinhgioi, tiếp tục truyền cảm hứng học tập cho học sinh cấp 3 thông qua các bài giảng súc tích, thực tiễn và giàu nhiệt huyết.